Mathematics (Core)
Paper 1 | Objectives | 49 Questions
WASSCE/WAEC MAY/JUNE
Year: 2016
Level: SHS
Time:
Type: Question Paper
Answers provided
FREE
No description provided
Feedbacks
This paper is yet to be rated
Paper 1 | Objectives | 49 Questions
WASSCE/WAEC MAY/JUNE
Year: 2016
Level: SHS
Time:
Type: Question Paper
Answers provided
No description provided
This paper is yet to be rated
| # | Question | Ans |
|---|---|---|
| 1. |
If 23x + 101x = 130x, find the value of x A. 7 B. 6 C. 5 D. 4 Detailed Solution23x + 101x = 130x2 x X1 + 3 x Xo + 1 x X2 + 0 x X1 + 1 x Xo = 1 x Xo = 1 x X2 + 3 x X1 + 0 x Xo = X2 + 3x + 0 2x + 3 = x2 + 0 + 1 + x2 + 3x 2x - 3x + x2 - x2 = -3 - 1 - x = -4 x = 4 |
|
| 2. |
Simplify: (\(\frac{3}{4} - \frac{2}{3}\)) x 1\(\frac{1}{5}\) A. \(\frac{1}{60}\) B. \(\frac{5}{72}\) C. \(\frac{1}{10}\) D. 1\(\frac{7}{10}\) Detailed Solution(\(\frac{3}{4} - \frac{2}{3}\)) x 1\(\frac{1}{5}\)= (\(\frac{9 - 8}{12} \times \frac{6}{5}\)) = \(\frac{1}{12} \times \frac{6}{5}\) = \(\frac{1}{10}\) |
|
| 3. |
Simplify:(\(\frac{10\sqrt{3}}{\sqrt{5}} - \sqrt{15}\))2 A. 75.00 B. 15.00 C. 8.66 D. 3.87 Detailed SolutionNote that \(\frac{10\sqrt{3}}{\sqrt{5}} = \frac{10\sqrt{3}}{\sqrt{5}} \times - \frac{\sqrt{5}}{\sqrt{5}}\)= \(\frac{10\sqrt{15}}{\sqrt{5}} = 2\sqrt{15}\) hence, (\(\frac{10\sqrt{3}}{\sqrt{5}} - \sqrt{15}\))2 = (\(2\sqrt{15} - \sqrt{15}\))2 = (\(2\sqrt{15} - \sqrt{15}\))(\(2\sqrt{15} - \sqrt{15}\)) = 4\(\sqrt{15 \times 15} - 2\sqrt{15 \times 15} - 2\sqrt{15 x 15} + \sqrt{15 \times 15}\) = 4 x 15 - 2 x 15 - 2 x 15 + 15 = 60 - 30 - 30 + 15 = 15 |
|
| 4. |
The distance, d, through which a stone falls from rest varies directly as the square of the time, t, taken. If the stone falls 45cm in 3 seconds, how far will it fall in 6 seconds? A. 90cm B. 135cm C. 180cm D. 225cm Detailed Solutiond \(\alpha\) t2d = t2 k where k is a constant. d = 45cm, when t = 3s; thus 45 = 32 x t k = \(\frac{45}{9}\) = 5 thus equation connecting d and t is d = 5t2 when t = 6s, d = 5 x 62 = 5 x 36 = 180cm |
|
| 5. |
Which of following is a valid conclusion from the premise. "Nigeria footballers are good footballers"? A. Joseph plays football in Nigeria therefore he is a good footballer B. Joseph is a good footballer therefore he is a Nigerian footballer C. Joseph is a Nigerian footballer therefore he is a good footballer D. Joseph plays good football therefore he is a Nigerian footballer Detailed Solution
 |
|
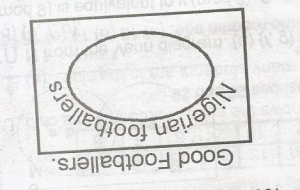| 6. |
On a map, 1cm represent 5km. Find the area on the map that represents 100km2. A. 2cm2 B. 4cm2 C. 8cm2 D. 8cm2 Detailed SolutionOn a map, 1cm represents 5km. Then it follows that 1cm2 represents 25km2. Acm2 represents 100km2. By apparent cross-multiplication, 1cm2 x 100km2 = Acm2x 25km2therefore A = \(\frac{100}{25}\) = 4cm2 |
|
| 7. |
Simplify; \(\frac{3^{n - 1} \times 27^{n + 1}}{81^{n}}\) A. 32n B. 9 C. 3n D. 3n + 1 Detailed Solution\(\frac{3^{n - 1} \times 27^{n + 1}}{81^{n}}\)= \(\frac{3^{n - 1} \times 3^{3(n + 1)}}{3^{4n}}\) = 3\(^{n - 1 + 3n + 3 - 4n}\) = 3\(^{4n - 4n - 1 + 3}\) = 32 = 9 |
|
| 8. |
What sum of money will amount to D10,400 in 5 years at 6% simple interest? A. D8,000.00 B. D10,000.00 C. D12,000.00 D. D16,000.00 Detailed SolutionA = P + 1I = A - P = 10,400 - P Now using I = \(\frac{P \times T \times R}{100}\) i.e. 10,400 - P = \(\frac{P \times 5 \times 6}{100}\) = 100(10,400 - P) = 30P 10(10,400 - P) = 3P 104,000 - 10P = 3P 104,000 - 10P = 3P 104,000 = 3P + 10P = 104,000 = 13P P = \(\frac{104,000}{100}\) P = D8,000 |
|
| 9. |
The roots of a quadratic equation are \(\frac{4}{3}\) and -\(\frac{3}{7}\). Find the equation A. 21x2 - 19x - 12 = 0 B. 21x2 + 37x - 12 = 0 C. 21x2 - x + 12 = 0 D. 21x2 + 7x - 4 = 0 Detailed SolutionLet x = \(\frac{4}{3}\), x = -\(\frac{3}{7}\)Then 3x = 4, 7x = -3 3x - 4 = 0, 7x + 3 = 0 (3x - 4)(7x + 3) = 0 21x2 + 9x - 28x - 12 = 0 21x2 - 19x - 12 = 0 |
|
| 10. |
Find the values of y for which the expression \(\frac{y^2 - 9y + 18}{y^2 + 4y - 21}\) is undefined A. 6, -7 B. 3, -6 C. 3, -7 D. -3, -7 Detailed Solution\(\frac{y^2 - 9y + 18}{y^2 + 4y - 21}\)Factorize the denominator; Y2 + 7y - 3y - 21 = y(y + 7) -3 (y + 7) = (y - 3)(y + 7) Hence the expression \(\frac{y^2 - 9y + 18}{y^2 + 4y - 21}\) is undefined when y2 + 4y - 21 = 0 ie. y = 3 or -7 |
Preview displays only 10 out of the 49 Questions
