
Mathematics (Core)
Paper 1 | Objectives | 48 Questions
WASSCE/WAEC MAY/JUNE
Year: 1995
Level: SHS
Time:
Type: Question Paper
Answers provided
FREE
No description provided
Feedbacks
This paper is yet to be rated

Paper 1 | Objectives | 48 Questions
WASSCE/WAEC MAY/JUNE
Year: 1995
Level: SHS
Time:
Type: Question Paper
Answers provided
No description provided
This paper is yet to be rated
Past questions are effective for revisions for all tests including WAEC, BECE, SAT, TOEFL, GCSE, IELTS
The goal of mocks tests is to create a bench-marking tool to help students assess their performances.
DAAD scholarship to assist Sub-Saharan African students fleeing war in Ukraine to complete their studies
| # | Question | Ans |
|---|---|---|
| 1. |
Find (101\(_2\))\(^2\), expressing the answer in base 2. A. 10101 B. 11001 C. 10010 D. 11101 E. 10110
Show Content
Detailed SolutionYou can convert it to base 10 and square, then re-convert it after the operation.OR You can multiply it straight applying the rules of binary multiplication. |
|
| 2. |
If three children shares N10.50 among themselves in ratio 6:7:8, how much is the largest share? A. N3.00 B. N3.50 C. N4.00 D. N4.50 E. N5.00
Show Content
Detailed SolutionRatio = 6 + 7 + 8 = 2121 = N10.50 1 = 1050K/21 = 50K 6 = 6 x 50K = N3.00 7 = 7 x 50K = N3.50 8 = 8 x 50K = N4.00 the Largest share = N4.00 |
|
| 3. |
Express 0.000834 in standard form A. 8.34 x 10-4 B. 8.34 x 10-3 C. 8.34 x 103 D. 8.34 x 104 E. 8.34 x 106 |
A |
| 4. |
Given that log2a = log84, find a A. 21/3 B. 42/3 C. 42/3 D. 22/3 E. 23
Show Content
Detailed SolutionLog2a = Log84Log2a = Log882/3 → 2/3Log88 → 2/3 x 1 Log2a = 2/3 Recall; If Logax = y ∴ ay = x Log2a = 2/3 22/3 = a |
|
| 5. |
By selling some crates of soft drinks for N600.00, a dealer makes a profit of 50%. How much did the dealer pay for the drinks? A. N1,200.00 B. N900.00 C. N450.00 D. N400.00 E. N200.00
Show Content
Detailed SolutionS.P = N600.00(100 + 50)% = N600 150% = N600 1% = \(\frac{600}{150}\) 100% = \(\frac{600}{150} \times 100%\) = N400 |
|
| 6. |
Find the nth term Un of the A.P., 11, 4, -3,....... . A. Un=19+7n B. Un=19-7n C. Un=18+7n D. Un= 18-7n E. Un= 17-7n
Show Content
Detailed SolutionA.P 11, 4, -31st term = 11 A.P = a, a + d, a + 2d ...... a + (n - 1)d If a = 11 a + d = 4 d = 4 - 11 = -7 nth term = a + (n-1)d = 11 + (n-1)(-7) = 11 - 7n + 7 = 18 - 7n |
|
| 7. |
Lf 16/9 , x, 1, y are in Geometric Progression (GP), find the product of x and y. A. 9/16 B. 3/4 C. 1 D. 4/3 E. 16/6
Show Content
Detailed Solution16/9, x, 1, y => a, ar, ar2, ar3ar2 = 1 => 16r2/9 = 1 => 16r2 9 => r2 = 9/16 => r = 3/4 ar2 = y = ar2 x r = 1 x 3/4 = 3/4 x xy = 4/3 x 3/4 = 1 |
|
| 8. |
If R = [2, 4, 6, 7] and S = [1, 2, 4, 8], then R∪S equal A. [1,2,4,6,7,8] B. [1,2,4,7,8] C. [1,4.7,8] D. [2.6.7] E. [2.4]
Show Content
Detailed SolutionR = {2, 4, 6, 7}; S = {1, 2, 4, 8}R \(\cup\) S = {1, 2, 4, 6, 7, 8} |
|
| 9. |
Find the value(s) of x for which the expression is undefined: \(\frac{6x - 1}{x^2 + 4x - 5}\) A. +4 or+1 B. -5 or +1 C. -5 or -1 D. +5 or -1 E. \(\frac{1}{6}\)
Show Content
Detailed Solution\(\frac{6x - 1}{x^2 + 4x - 5}\)The expression is undefined when \(x^2 + 4x - 5 = 0\) \(x^2 + 5x - x - 5 = 0\) \(x(x + 5) - 1(x + 5) = 0\) \((x - 1)(x + 5) = 0\) The expression is undefined when x = 1 or -5. |
|
| 10. |
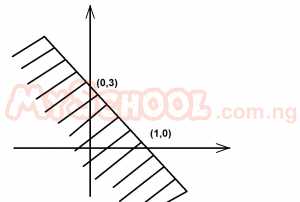 Which of the following could be the inequality illustrated in the sketch graph above? A. y≥2x+3 B. y≤-3x+3 C. y < 3x+2 D. y≤x +3 E. y≥3x+2.
Show Content
Detailed SolutionGradient of the line = \(\frac{3 - 0}{0 - 1}\)= -3 y = -3x + b. Using (1,0), we have 0 = -3(1) + b 0 = -3 + b b = 3 y = -3x + 3 \(\therefore\) The graph illustrates y \(\leq\) -3x + 3. |
Preview displays only 10 out of the 48 Questions