
Mathematics (Core)
Paper 1 | Objectives | 49 Questions
WASSCE/WAEC MAY/JUNE
Year: 2002
Level: SHS
Time:
Type: Question Paper
Answers provided
FREE
No description provided
Feedbacks
This paper is yet to be rated

Paper 1 | Objectives | 49 Questions
WASSCE/WAEC MAY/JUNE
Year: 2002
Level: SHS
Time:
Type: Question Paper
Answers provided
No description provided
This paper is yet to be rated
How can past papers boost your revision? See how practicing past test is a good way to get higher grades.
These are the best study techniques and methods that get higher grades in any school tests or exams.
Tips to make the best study space and quality time for studies are essential.
| # | Question | Ans |
|---|---|---|
| 1. |
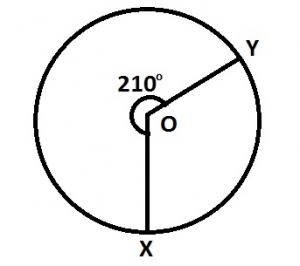 In the diagram O is the center of the circle. Reflex angle XOY = 210° and the length of the minor arc is 5.5m. Find, correct to the nearest meter, the length of the major arc. A. 8m B. 9m C. 10m D. 13m
Show Content
Detailed SolutionGiven, Length of minor arc = 5.5mAngle subtended by minor arc = 360° - 210° = 150° \(\therefore 5.5 = \frac{150}{360} \times 2 \times \frac{22}{7} \times r \) \(\frac{55r}{21} = 5.5\) \(r = \frac{5.5 \times 21}{55}\) r = 2.1m Length of major arc = \(\frac{210}{360} \times 2 \times \frac{22}{7} \times 2.1\) = \(7.7m \approxeq 8m\) (to the nearest metre) |
|
| 2. |
A right pyramid is on a square base of side 4cm. The slanting side of the pyramid is \(2\sqrt{3}\) cm. Calculate the volume of the pyramid A. \(5\frac{1}{3}cm^3\) B. \(10\frac{2}{3}cm^3\) C. \(16cm^3\) D. \(32cm^3\)
Show Content
Detailed Solution \(BD^2 = 4^2 + 4^2\) \(BD = \sqrt{16 + 16} = \sqrt{32}\) \(BD = 4\sqrt{2} cm\)  \((2\sqrt{3})^2 = (2\sqrt{2})^2 + h^2\) \(h^2 = 12 - 8 = 4\) \(h = \sqrt{4} = 2 cm\) Volume of pyramid = \(\frac{a^2 h}{3}\) = \(\frac{4^2 \times 2}{3}\) = \(\frac{32}{3} = 10\frac{2}{3} cm^3\) |
|
| 3. |
The height of a right circular cone is 4cm. The radius of its base is 3cm. Find the curved surface area A. \(9\pi cm^2\) B. \(15\pi cm^2\) C. \(16\pi cm^2\) D. \(20\pi cm^2\)
Show Content
Detailed SolutionCurved surface area or a cone \(=\pi rl\)from the information \(l^2 = 4^2 + 3^2 = 16+9\\ l = \sqrt{25} = 5; ∴ C.S.A\hspace{1mm} = \frac{22}{7}\times 3 \times 5\\ Since \frac{22}{7}=\pi ∴ C.S.A\hspace{1mm} =\hspace{1mm}15\pi\) |
|
| 4. |
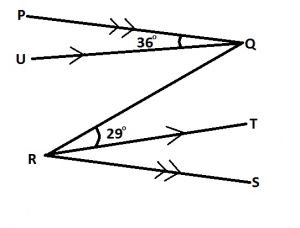 In the diagram above, ∠PQU=36°, ∠QRT = 29°, PQ||RT. Find ∠PQR A. 94o B. 65o C. 61o D. 54o
Show Content
Detailed Solution< UQR = 29° (alternate angles)< PQR = < PQU + < UQR = 36° + 29° = 65° |
|
| 5. |
Simplify \(5\frac{1}{4}\div \left(1\frac{2}{3}- \frac{1}{2}\right)\) A. \(1\frac{3}{4}\) B. \(3\frac{1}{2}\) C. \(4\frac{1}{2}\) D. \(8\frac{1}{2}\)
Show Content
Detailed Solution\(5\frac{1}{4}\div \left(1\frac{2}{3}- \frac{1}{2}\right)\\\frac{21}{4}\div \left(1\frac{4-3}{6}\right)\\ \frac{21}{4}\div \left(1\frac{1}{6}\right)\\ \frac{21}{4} \times \frac{6}{7}= 4\frac{1}{2}\) |
|
| 6. |
Find the value of x in 0.5x + 2.6 = 5x + 0.35 A. 0.5 B. 2 C. 2.6 D. 5
Show Content
Detailed Solution\(0.5x + 2.6 = 5x + 0.35\\0.5x - 5x = 0.35-2.6\\ -4.5x = -2.25\\ x = \frac{-2.25}{-4.5}\\ 0.5\) |
|
| 7. |
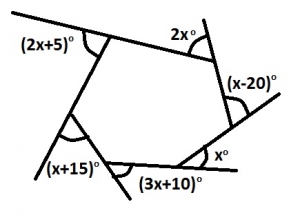 Find the value of x in the diagram A. 31o B. 35o C. 37o D. 41o
Show Content
Detailed SolutionSum of exterior angle of any polygon is 360o(2x+5)o + 2xo + (x-20)o + xo + (3x+10)o + (x + 15)o = 360o; 10x = 350 x = 35 |
|
| 8. |
If \(M5_{ten} = 1001011_{two}\) find the value of M A. 5 B. 6 C. 7 D. 8
Show Content
Detailed Solution\(M5_{ten} = 1001011_{two}\\=1 \times 2^6 + 0\times 2^5 + 0\times 2^4 + 1\times 2^3 + 0\times 2^2 + 1\times 2^1 \\ =64+8+2+1=75_{ten}\\ ∴ m = 7 \) |
|
| 9. |
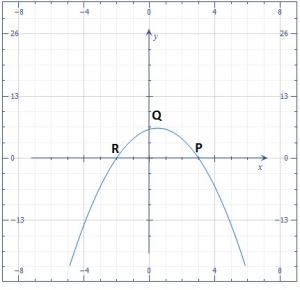 The diagram is the graph of \(y = 6 + x - x^2\). The graph intercepts the x- axis at P and R and the y- axis at Q.What is the value of y at Q? A. \(6\frac{1}{3}\) B. 6 C. 3 D. zero |
A |
| 10. |
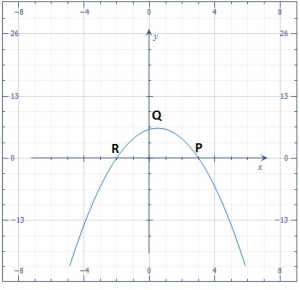 The diagram is the graph of \(y = 6 + x - x^2\). The graph intercepts the x- axis at P and R and the y- axis at Q.When \(y = 3\frac{1}{3}\), what is the positive value of x? A. \( 2\frac{1}{2}\) B. \( 2\frac{1}{5}\) C. \( 1\frac{1}{5}\) D. zero |
B |
Preview displays only 10 out of the 49 Questions