Year :
2002
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
1 - 10 of 49 Questions
| # | Question | Ans |
|---|---|---|
| 1. |
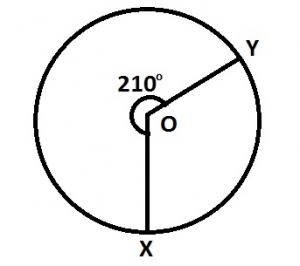 In the diagram O is the center of the circle. Reflex angle XOY = 210° and the length of the minor arc is 5.5m. Find, correct to the nearest meter, the length of the major arc. A. 8m B. 9m C. 10m D. 13m Detailed SolutionGiven, Length of minor arc = 5.5mAngle subtended by minor arc = 360° - 210° = 150° \(\therefore 5.5 = \frac{150}{360} \times 2 \times \frac{22}{7} \times r \) \(\frac{55r}{21} = 5.5\) \(r = \frac{5.5 \times 21}{55}\) r = 2.1m Length of major arc = \(\frac{210}{360} \times 2 \times \frac{22}{7} \times 2.1\) = \(7.7m \approxeq 8m\) (to the nearest metre) |
|
| 2. |
A right pyramid is on a square base of side 4cm. The slanting side of the pyramid is \(2\sqrt{3}\) cm. Calculate the volume of the pyramid A. \(5\frac{1}{3}cm^3\) B. \(10\frac{2}{3}cm^3\) C. \(16cm^3\) D. \(32cm^3\) Detailed Solution \(BD^2 = 4^2 + 4^2\) \(BD = \sqrt{16 + 16} = \sqrt{32}\) \(BD = 4\sqrt{2} cm\)  \((2\sqrt{3})^2 = (2\sqrt{2})^2 + h^2\) \(h^2 = 12 - 8 = 4\) \(h = \sqrt{4} = 2 cm\) Volume of pyramid = \(\frac{a^2 h}{3}\) = \(\frac{4^2 \times 2}{3}\) = \(\frac{32}{3} = 10\frac{2}{3} cm^3\) |
|
| 3. |
The height of a right circular cone is 4cm. The radius of its base is 3cm. Find the curved surface area A. \(9\pi cm^2\) B. \(15\pi cm^2\) C. \(16\pi cm^2\) D. \(20\pi cm^2\) Detailed SolutionCurved surface area or a cone \(=\pi rl\)from the information \(l^2 = 4^2 + 3^2 = 16+9\\ l = \sqrt{25} = 5; ∴ C.S.A\hspace{1mm} = \frac{22}{7}\times 3 \times 5\\ Since \frac{22}{7}=\pi ∴ C.S.A\hspace{1mm} =\hspace{1mm}15\pi\) |
|
| 4. |
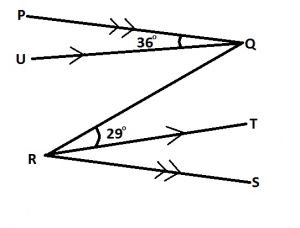 In the diagram above, ∠PQU=36°, ∠QRT = 29°, PQ||RT. Find ∠PQR A. 94o B. 65o C. 61o D. 54o Detailed Solution< UQR = 29° (alternate angles)< PQR = < PQU + < UQR = 36° + 29° = 65° |
|
| 5. |
Simplify \(5\frac{1}{4}\div \left(1\frac{2}{3}- \frac{1}{2}\right)\) A. \(1\frac{3}{4}\) B. \(3\frac{1}{2}\) C. \(4\frac{1}{2}\) D. \(8\frac{1}{2}\) Detailed Solution\(5\frac{1}{4}\div \left(1\frac{2}{3}- \frac{1}{2}\right)\\\frac{21}{4}\div \left(1\frac{4-3}{6}\right)\\ \frac{21}{4}\div \left(1\frac{1}{6}\right)\\ \frac{21}{4} \times \frac{6}{7}= 4\frac{1}{2}\) |
|
| 6. |
Find the value of x in 0.5x + 2.6 = 5x + 0.35 A. 0.5 B. 2 C. 2.6 D. 5 Detailed Solution\(0.5x + 2.6 = 5x + 0.35\\0.5x - 5x = 0.35-2.6\\ -4.5x = -2.25\\ x = \frac{-2.25}{-4.5}\\ 0.5\) |
|
| 7. |
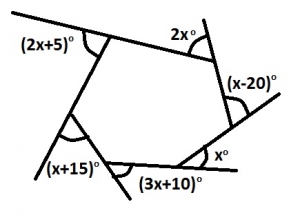 Find the value of x in the diagram A. 31o B. 35o C. 37o D. 41o Detailed SolutionSum of exterior angle of any polygon is 360o(2x+5)o + 2xo + (x-20)o + xo + (3x+10)o + (x + 15)o = 360o; 10x = 350 x = 35 |
|
| 8. |
If \(M5_{ten} = 1001011_{two}\) find the value of M A. 5 B. 6 C. 7 D. 8 Detailed Solution\(M5_{ten} = 1001011_{two}\\=1 \times 2^6 + 0\times 2^5 + 0\times 2^4 + 1\times 2^3 + 0\times 2^2 + 1\times 2^1 \\ =64+8+2+1=75_{ten}\\ ∴ m = 7 \) |
|
| 9. |
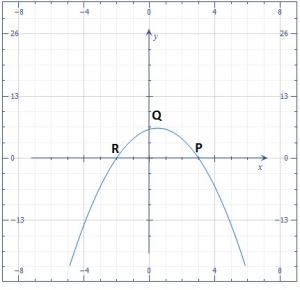 The diagram is the graph of \(y = 6 + x - x^2\). The graph intercepts the x- axis at P and R and the y- axis at Q.What is the value of y at Q? A. \(6\frac{1}{3}\) B. 6 C. 3 D. zero |
A |
| 10. |
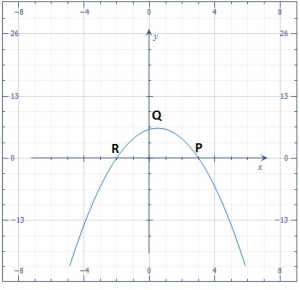 The diagram is the graph of \(y = 6 + x - x^2\). The graph intercepts the x- axis at P and R and the y- axis at Q.When \(y = 3\frac{1}{3}\), what is the positive value of x? A. \( 2\frac{1}{2}\) B. \( 2\frac{1}{5}\) C. \( 1\frac{1}{5}\) D. zero |
B |
| 1. |
 In the diagram O is the center of the circle. Reflex angle XOY = 210° and the length of the minor arc is 5.5m. Find, correct to the nearest meter, the length of the major arc. A. 8m B. 9m C. 10m D. 13m Detailed SolutionGiven, Length of minor arc = 5.5mAngle subtended by minor arc = 360° - 210° = 150° \(\therefore 5.5 = \frac{150}{360} \times 2 \times \frac{22}{7} \times r \) \(\frac{55r}{21} = 5.5\) \(r = \frac{5.5 \times 21}{55}\) r = 2.1m Length of major arc = \(\frac{210}{360} \times 2 \times \frac{22}{7} \times 2.1\) = \(7.7m \approxeq 8m\) (to the nearest metre) |
|
| 2. |
A right pyramid is on a square base of side 4cm. The slanting side of the pyramid is \(2\sqrt{3}\) cm. Calculate the volume of the pyramid A. \(5\frac{1}{3}cm^3\) B. \(10\frac{2}{3}cm^3\) C. \(16cm^3\) D. \(32cm^3\) Detailed Solution \(BD^2 = 4^2 + 4^2\) \(BD = \sqrt{16 + 16} = \sqrt{32}\) \(BD = 4\sqrt{2} cm\)  \((2\sqrt{3})^2 = (2\sqrt{2})^2 + h^2\) \(h^2 = 12 - 8 = 4\) \(h = \sqrt{4} = 2 cm\) Volume of pyramid = \(\frac{a^2 h}{3}\) = \(\frac{4^2 \times 2}{3}\) = \(\frac{32}{3} = 10\frac{2}{3} cm^3\) |
|
| 3. |
The height of a right circular cone is 4cm. The radius of its base is 3cm. Find the curved surface area A. \(9\pi cm^2\) B. \(15\pi cm^2\) C. \(16\pi cm^2\) D. \(20\pi cm^2\) Detailed SolutionCurved surface area or a cone \(=\pi rl\)from the information \(l^2 = 4^2 + 3^2 = 16+9\\ l = \sqrt{25} = 5; ∴ C.S.A\hspace{1mm} = \frac{22}{7}\times 3 \times 5\\ Since \frac{22}{7}=\pi ∴ C.S.A\hspace{1mm} =\hspace{1mm}15\pi\) |
|
| 4. |
 In the diagram above, ∠PQU=36°, ∠QRT = 29°, PQ||RT. Find ∠PQR A. 94o B. 65o C. 61o D. 54o Detailed Solution< UQR = 29° (alternate angles)< PQR = < PQU + < UQR = 36° + 29° = 65° |
|
| 5. |
Simplify \(5\frac{1}{4}\div \left(1\frac{2}{3}- \frac{1}{2}\right)\) A. \(1\frac{3}{4}\) B. \(3\frac{1}{2}\) C. \(4\frac{1}{2}\) D. \(8\frac{1}{2}\) Detailed Solution\(5\frac{1}{4}\div \left(1\frac{2}{3}- \frac{1}{2}\right)\\\frac{21}{4}\div \left(1\frac{4-3}{6}\right)\\ \frac{21}{4}\div \left(1\frac{1}{6}\right)\\ \frac{21}{4} \times \frac{6}{7}= 4\frac{1}{2}\) |
| 6. |
Find the value of x in 0.5x + 2.6 = 5x + 0.35 A. 0.5 B. 2 C. 2.6 D. 5 Detailed Solution\(0.5x + 2.6 = 5x + 0.35\\0.5x - 5x = 0.35-2.6\\ -4.5x = -2.25\\ x = \frac{-2.25}{-4.5}\\ 0.5\) |
|
| 7. |
 Find the value of x in the diagram A. 31o B. 35o C. 37o D. 41o Detailed SolutionSum of exterior angle of any polygon is 360o(2x+5)o + 2xo + (x-20)o + xo + (3x+10)o + (x + 15)o = 360o; 10x = 350 x = 35 |
|
| 8. |
If \(M5_{ten} = 1001011_{two}\) find the value of M A. 5 B. 6 C. 7 D. 8 Detailed Solution\(M5_{ten} = 1001011_{two}\\=1 \times 2^6 + 0\times 2^5 + 0\times 2^4 + 1\times 2^3 + 0\times 2^2 + 1\times 2^1 \\ =64+8+2+1=75_{ten}\\ ∴ m = 7 \) |
|
| 9. |
 The diagram is the graph of \(y = 6 + x - x^2\). The graph intercepts the x- axis at P and R and the y- axis at Q.What is the value of y at Q? A. \(6\frac{1}{3}\) B. 6 C. 3 D. zero |
A |
| 10. |
 The diagram is the graph of \(y = 6 + x - x^2\). The graph intercepts the x- axis at P and R and the y- axis at Q.When \(y = 3\frac{1}{3}\), what is the positive value of x? A. \( 2\frac{1}{2}\) B. \( 2\frac{1}{5}\) C. \( 1\frac{1}{5}\) D. zero |
B |