Year : 
2004
Title : 
Mathematics (Core)
Exam : 
WASSCE/WAEC MAY/JUNE

Paper 1 | Objectives

41 - 50 of 50 Questions

# Question Ans
41.

The values of x when y = 3 are approximately

A. -4.7 and 1.4

B. -4.6 and 1.5

C. -3.6 and 0.4

D. -3.6 and 1.5

B
42.

Which of the following quadratic equations has \(-\frac{1}{2}\) and \(\frac{3}{4}\) as its roots?

A. 8x2 + 11x - 3 = 0

B. 8x2 -11x – 3 = 0

C. 8x2 + 2x -3 = 0

D. 8x2 - 2x – 3 = 0

Detailed Solution

X2 - (sum of the roots)x + (product of the roots) = 0
Sum of the roots \(= -\frac{1}{2}+\frac{3}{4} = \frac{-2+3}{2}=\frac{1}{4}\)
Product of the roots = \(-\frac{1}{2}\times \frac{3}{4}=\frac{-3}{8}\\
X^2-\left(\frac{1}{4}\right)x-\frac{3}{8} = 0. Taking \hspace{1mm}the\hspace{1mm} common\)
\(8x^2-2x-3=0\);
43.

The locus of a point which moves in a plane such that it is equidistant from two fixed points X and Y is

A. the perpendicular bisector of the line segment X Y

B. a line parallel to the line segment XY

C. a circle with XY as diameter

D. the line perpendicular to the line segment XY

A
44.

Given that \(P\propto \frac{1}{\sqrt{r}}\) and p = 3 when r = 16, find the value of r when p =-5

A. 48

B. 64

C. 72

D. 324

Detailed Solution

\(P \propto \frac{1}{\sqrt{r}} P=3\hspace{1mm}r=16\\
P = \frac{k}{\sqrt{r}}\Rightarrow 3 = \frac{k}{\sqrt{16}}\Rightarrow \frac{3}{1} = \frac{k}{4} \\ \Rightarrow K = 12 \Rightarrow K = 12; P\sqrt{r} = k \Rightarrow \sqrt{r} = \frac{k}{p}\\
r = \frac{(k)^2}{P}=12^2 \div \frac{3}{2}=\left(\frac{12}{1}\times \frac{2}{3}\right)=8^2\\
r = 64\)
45.

Which of the following is/are true? In a plane, the locus of points I. Equidistant from a straight line is a circle radius d where d is the distance between the point and the straight line.
II Equidistant from two given points P and Q is a circle of radius |PQ|. III Equidistant from two points is the perpendicular bisector of the line joining the two points.

A. I only

B. II only

C. III only

D. I, II and III

C
46.

The sides of two cubes are in the ratio 2:5. What is the ratio of their volumes?

A. 4:5

B. 8: 15

C. 6:125

D. 8:125

Detailed Solution

The ratio of the two cubes = 2:5
Volume of the two cubes = 2\(^3\) : 5\(^3\) = 8 : 125
47.

Given that p = 2, q = -5 and r = - 4, evaluate 3p2 - q2 - r3

A. 101

B. 77

C. 51

D. -27

Detailed Solution

3(2)2 - (-5)2 - (-4)3
3(4) – (25) – (-64); 12 – 25 + 64 = 51
48.

A Cooperative Society, charges an interest of 51/2% per annum on any amount borrowed by its members. If a member borrows N125,000, how much does he pay back after one year?

A. N136875

B. N131,875

C. N126750

D. N126250

Detailed Solution

The rate of interest charge = 51/2% p.a
The amount borrowed = N125, 000:00
Interest charge \(=\frac{11}{200} of N125,000\\
= 11 \times N625.00 = N6,875.00\)
The amount refunded by the member with interest charge by the cooperative society
N125,000+N6,875.00 = N131,875.00
49.

A bag contains 3 red and 2 white identical balls. lf 2 balls are picked at random from the bag, one after the other and with replacement, find the probability that they are of different colours

A. \(\frac{36}{625}\)

B. \(\frac{16}{625}\)

C. \(\frac{12}{25}\)

D. \(\frac{13}{25}\)

Detailed Solution

Prob(RW or WR) = Prob(RW) + Prob(WR)
\(Prob(R) = \frac{3}{5}:Prob(W) = \frac{2}{5}\\
Prob(RW\hspace{1mm}or\hspace{1mm}WR)=\frac{3}{5}\times\frac{2}{5}+\frac{2}{5}\times \frac{3}{5}\\
\frac{6}{25}+\frac{6}{25}=\frac{12}{25}\)
50.

A point on the ground is 5m away from the foot of a vertical wall 7 m high, Calculate, correct to the nearest degree, the angle of depression of the point from the top of the wall

A. 36o

B. 44o

C. 46o

D. 54o

Detailed Solution

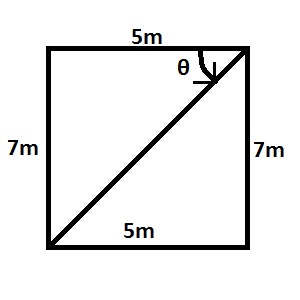θ= angle of depression of the point from the top of the wall
\(tan\theta = \frac{7}{5}=1.4; \theta = tan^{-1}(1.400)\
\theta = 54.4^{\circ}; \theta = 54^{\circ}\) to the nearest degree
41.

The values of x when y = 3 are approximately

A. -4.7 and 1.4

B. -4.6 and 1.5

C. -3.6 and 0.4

D. -3.6 and 1.5

B
42.

Which of the following quadratic equations has \(-\frac{1}{2}\) and \(\frac{3}{4}\) as its roots?

A. 8x2 + 11x - 3 = 0

B. 8x2 -11x – 3 = 0

C. 8x2 + 2x -3 = 0

D. 8x2 - 2x – 3 = 0

Detailed Solution

X2 - (sum of the roots)x + (product of the roots) = 0
Sum of the roots \(= -\frac{1}{2}+\frac{3}{4} = \frac{-2+3}{2}=\frac{1}{4}\)
Product of the roots = \(-\frac{1}{2}\times \frac{3}{4}=\frac{-3}{8}\\
X^2-\left(\frac{1}{4}\right)x-\frac{3}{8} = 0. Taking \hspace{1mm}the\hspace{1mm} common\)
\(8x^2-2x-3=0\);
43.

The locus of a point which moves in a plane such that it is equidistant from two fixed points X and Y is

A. the perpendicular bisector of the line segment X Y

B. a line parallel to the line segment XY

C. a circle with XY as diameter

D. the line perpendicular to the line segment XY

A
44.

Given that \(P\propto \frac{1}{\sqrt{r}}\) and p = 3 when r = 16, find the value of r when p =-5

A. 48

B. 64

C. 72

D. 324

Detailed Solution

\(P \propto \frac{1}{\sqrt{r}} P=3\hspace{1mm}r=16\\
P = \frac{k}{\sqrt{r}}\Rightarrow 3 = \frac{k}{\sqrt{16}}\Rightarrow \frac{3}{1} = \frac{k}{4} \\ \Rightarrow K = 12 \Rightarrow K = 12; P\sqrt{r} = k \Rightarrow \sqrt{r} = \frac{k}{p}\\
r = \frac{(k)^2}{P}=12^2 \div \frac{3}{2}=\left(\frac{12}{1}\times \frac{2}{3}\right)=8^2\\
r = 64\)
45.

Which of the following is/are true? In a plane, the locus of points I. Equidistant from a straight line is a circle radius d where d is the distance between the point and the straight line.
II Equidistant from two given points P and Q is a circle of radius |PQ|. III Equidistant from two points is the perpendicular bisector of the line joining the two points.

A. I only

B. II only

C. III only

D. I, II and III

C
46.

The sides of two cubes are in the ratio 2:5. What is the ratio of their volumes?

A. 4:5

B. 8: 15

C. 6:125

D. 8:125

Detailed Solution

The ratio of the two cubes = 2:5
Volume of the two cubes = 2\(^3\) : 5\(^3\) = 8 : 125
47.

Given that p = 2, q = -5 and r = - 4, evaluate 3p2 - q2 - r3

A. 101

B. 77

C. 51

D. -27

Detailed Solution

3(2)2 - (-5)2 - (-4)3
3(4) – (25) – (-64); 12 – 25 + 64 = 51
48.

A Cooperative Society, charges an interest of 51/2% per annum on any amount borrowed by its members. If a member borrows N125,000, how much does he pay back after one year?

A. N136875

B. N131,875

C. N126750

D. N126250

Detailed Solution

The rate of interest charge = 51/2% p.a
The amount borrowed = N125, 000:00
Interest charge \(=\frac{11}{200} of N125,000\\
= 11 \times N625.00 = N6,875.00\)
The amount refunded by the member with interest charge by the cooperative society
N125,000+N6,875.00 = N131,875.00
49.

A bag contains 3 red and 2 white identical balls. lf 2 balls are picked at random from the bag, one after the other and with replacement, find the probability that they are of different colours

A. \(\frac{36}{625}\)

B. \(\frac{16}{625}\)

C. \(\frac{12}{25}\)

D. \(\frac{13}{25}\)

Detailed Solution

Prob(RW or WR) = Prob(RW) + Prob(WR)
\(Prob(R) = \frac{3}{5}:Prob(W) = \frac{2}{5}\\
Prob(RW\hspace{1mm}or\hspace{1mm}WR)=\frac{3}{5}\times\frac{2}{5}+\frac{2}{5}\times \frac{3}{5}\\
\frac{6}{25}+\frac{6}{25}=\frac{12}{25}\)
50.

A point on the ground is 5m away from the foot of a vertical wall 7 m high, Calculate, correct to the nearest degree, the angle of depression of the point from the top of the wall

A. 36o

B. 44o

C. 46o

D. 54o

Detailed Solution

θ= angle of depression of the point from the top of the wall
\(tan\theta = \frac{7}{5}=1.4; \theta = tan^{-1}(1.400)\
\theta = 54.4^{\circ}; \theta = 54^{\circ}\) to the nearest degree