Year :
2004
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
21 - 30 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 21. |
Find, correct to two decimal places, the mean of 9, 13, 16, 17, 19, 23, 24. A. 23.00 B. 17.29 C. 16.50 D. 16.33 Detailed SolutionMean \(= \frac{sum\hspace{1mm}of\hspace{1mm}all\hspace{1mm}the\hspace{1mm}numbers}{Total\hspace{1mm}Number}\\\frac{9+13+16+17+19+23+24}{7}\\ \frac{121}{7}=17.2857=17.29\) |
|
| 22. |
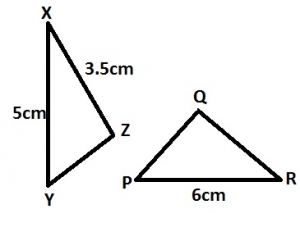 In the diagram, ∆XYZ is similar to ∆PRQ, |XY| = 5cm, |XZ| =3.5cm and |PR| = 8cm. Find |PQ| A. 5.6 cm B. 11.2cm C. 11.4cm D. 28.0cm Detailed Solution\(\frac{PQ}{PR}=\frac{XZ}{XY}; \frac{PQ}{8}=\frac{3.5}{5}\\PQ=\frac{8\times 3.5}{5}=\frac{28}{5}=5.6cm\) |
|
| 23. |
Factorise 27p2x2 - 48y2. A. 9(3px - 4y)2 B. 3(3px - 4y)(3px - 4y) C. 9(px - 4y)(3p x + 4y) D. 3(3px -4y)(3px +4y) Detailed Solution27p2x2 - 48y2; 3(32 p2x2-42y2)3[(3px) 2 - (4y) 2]; 3[(3px-4y)(3px+4y)] |
|
| 24. |
What is the volume of a solid cylinder of diameter 7cm and height 7cm? (Take \(\pi = \frac{22}{7}\)) A. 38.5cm3 B. 77cm3 C. 269.5cm3 D. 1078cm3 Detailed SolutionVolume of a solid cylinder = Base area x heightBase area \(=\pi r^2 =\frac{22}{7} \times \frac{7}{2}\times \frac{7}{2} = \frac{77}{2}\) Volume of a solid cylinder = \(\frac{77}{2}\times \frac{7}{1} = \frac{539}{2}cm^3\\ =269.5cm^3\) |
|
| 25. |
Find the sum of the roots of the equation 2x2 + 3x - 9 = 0 A. -18 B. -6 C. \(-\frac{9}{2}\) D. \(-\frac{3}{2}\) Detailed SolutionThe general quadratic equationx2 - (sum of roots) x + (product of root) = 0 Comparing with the given equation 2x2 +3x2 - 9 = 0; \(x^2 + \frac{3}{2}x - \frac{9}{2} = 0\\ Sum \hspace{1mm} of \hspace{1mm}roots = -\frac{3}{2}\) |
|
| 26. |
Given that ξ = {1, 2, 3, . . . . . . ,10}, P= (x : x is prime) and Q = {y : y is odd}, find Pl∩Q A. {2} B. {1,9} C. {315.7} D. {4, 6, 8, 10} Detailed Solutionξ = {1, 2, 3, . . . . . . ,10}, P= (2, 3, 5, 7) and Q = {1, 3, 5, 9},Pl∩Q = {1, 4, 6, 8, 9, 10}∩{1, 3, 5, 7, 9} = {1, 9} |
|
| 27. |
 In the diagram, KS is a tangent to the circle centre O at R and ∠ROQ = 80o. Find ∠QRS. A. 90o B. 80o C. 50o D. 40o Detailed Solution∠QRS = ∠RPQ (theorem: angle in the alternate segment are equal)∠RPQ = 50o ∠QRS = 50o |
|
| 28. |
Find the mean deviation of 6, 7, 8, 9, 10 A. 1.2 B. 1.5 C. 2 D. 8 Detailed Solution\(\begin{matrix}x & x-m & |x-m| \\ 6 & -2 & 2 \\ 7 & -1 & 1 \\ 8 & 0 & 0 \\ 9 & 1 & 1 \\ 10 & 2 & 2 \\ & & 6 \end{matrix} \) Mean deviation\(=\frac{\sum|x-m|}{n}=\frac{6}{5} = 1.2\) |
|
| 29. |
A point X is on the bearing 342o from a point Y. What is the bearing of Y from X? A. 342o B. 252o C. 198o D. 162o Detailed SolutionIf x is the bearing 342ofrom a point y= 360o - 342o = 18o; The bearing of y from x = 180o - 18o = 162o |
|
| 30. |
 In the diagram, O is the centre of the circle where OS//QR and ∠SOR = 35o A. 35o B. 45o C. 55o D. 70o Detailed Solution∠SOR = ∠ORQ alternate angle.Also ∠OQR = ∠OQR (Base angle of isosceles) ∠QOR = 108 – 2(35o) = 180 - 70o - 110o ∠QPR = 1/2QOR = 1/2(110o) ∠QPR + 55o (theorem angle at center is twice angle at circumference) |
| 21. |
Find, correct to two decimal places, the mean of 9, 13, 16, 17, 19, 23, 24. A. 23.00 B. 17.29 C. 16.50 D. 16.33 Detailed SolutionMean \(= \frac{sum\hspace{1mm}of\hspace{1mm}all\hspace{1mm}the\hspace{1mm}numbers}{Total\hspace{1mm}Number}\\\frac{9+13+16+17+19+23+24}{7}\\ \frac{121}{7}=17.2857=17.29\) |
|
| 22. |
 In the diagram, ∆XYZ is similar to ∆PRQ, |XY| = 5cm, |XZ| =3.5cm and |PR| = 8cm. Find |PQ| A. 5.6 cm B. 11.2cm C. 11.4cm D. 28.0cm Detailed Solution\(\frac{PQ}{PR}=\frac{XZ}{XY}; \frac{PQ}{8}=\frac{3.5}{5}\\PQ=\frac{8\times 3.5}{5}=\frac{28}{5}=5.6cm\) |
|
| 23. |
Factorise 27p2x2 - 48y2. A. 9(3px - 4y)2 B. 3(3px - 4y)(3px - 4y) C. 9(px - 4y)(3p x + 4y) D. 3(3px -4y)(3px +4y) Detailed Solution27p2x2 - 48y2; 3(32 p2x2-42y2)3[(3px) 2 - (4y) 2]; 3[(3px-4y)(3px+4y)] |
|
| 24. |
What is the volume of a solid cylinder of diameter 7cm and height 7cm? (Take \(\pi = \frac{22}{7}\)) A. 38.5cm3 B. 77cm3 C. 269.5cm3 D. 1078cm3 Detailed SolutionVolume of a solid cylinder = Base area x heightBase area \(=\pi r^2 =\frac{22}{7} \times \frac{7}{2}\times \frac{7}{2} = \frac{77}{2}\) Volume of a solid cylinder = \(\frac{77}{2}\times \frac{7}{1} = \frac{539}{2}cm^3\\ =269.5cm^3\) |
|
| 25. |
Find the sum of the roots of the equation 2x2 + 3x - 9 = 0 A. -18 B. -6 C. \(-\frac{9}{2}\) D. \(-\frac{3}{2}\) Detailed SolutionThe general quadratic equationx2 - (sum of roots) x + (product of root) = 0 Comparing with the given equation 2x2 +3x2 - 9 = 0; \(x^2 + \frac{3}{2}x - \frac{9}{2} = 0\\ Sum \hspace{1mm} of \hspace{1mm}roots = -\frac{3}{2}\) |
| 26. |
Given that ξ = {1, 2, 3, . . . . . . ,10}, P= (x : x is prime) and Q = {y : y is odd}, find Pl∩Q A. {2} B. {1,9} C. {315.7} D. {4, 6, 8, 10} Detailed Solutionξ = {1, 2, 3, . . . . . . ,10}, P= (2, 3, 5, 7) and Q = {1, 3, 5, 9},Pl∩Q = {1, 4, 6, 8, 9, 10}∩{1, 3, 5, 7, 9} = {1, 9} |
|
| 27. |
 In the diagram, KS is a tangent to the circle centre O at R and ∠ROQ = 80o. Find ∠QRS. A. 90o B. 80o C. 50o D. 40o Detailed Solution∠QRS = ∠RPQ (theorem: angle in the alternate segment are equal)∠RPQ = 50o ∠QRS = 50o |
|
| 28. |
Find the mean deviation of 6, 7, 8, 9, 10 A. 1.2 B. 1.5 C. 2 D. 8 Detailed Solution\(\begin{matrix}x & x-m & |x-m| \\ 6 & -2 & 2 \\ 7 & -1 & 1 \\ 8 & 0 & 0 \\ 9 & 1 & 1 \\ 10 & 2 & 2 \\ & & 6 \end{matrix} \) Mean deviation\(=\frac{\sum|x-m|}{n}=\frac{6}{5} = 1.2\) |
|
| 29. |
A point X is on the bearing 342o from a point Y. What is the bearing of Y from X? A. 342o B. 252o C. 198o D. 162o Detailed SolutionIf x is the bearing 342ofrom a point y= 360o - 342o = 18o; The bearing of y from x = 180o - 18o = 162o |
|
| 30. |
 In the diagram, O is the centre of the circle where OS//QR and ∠SOR = 35o A. 35o B. 45o C. 55o D. 70o Detailed Solution∠SOR = ∠ORQ alternate angle.Also ∠OQR = ∠OQR (Base angle of isosceles) ∠QOR = 108 – 2(35o) = 180 - 70o - 110o ∠QPR = 1/2QOR = 1/2(110o) ∠QPR + 55o (theorem angle at center is twice angle at circumference) |