Year :
2004
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
1 - 10 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 1. |
1. Evaluate \( 202^2_{three} - 112^2_{three}\) A. 21120 B. 21121 C. 21112 D. 21011 Detailed Solution\(202^2_{three}\)when converted to base ten \(=(202_3)^2\\202_3 = 2 \times 3^2 + 0 \times 3^1 + 2\times 3^0 = 18 + 0 + 2\\ =20_{ten}; (202_3)^2 = (20)^2_{ten} = 400\\ 112^2_{three}\)when converted to base ten \(= (112_3)^2\\ 112_3 = 1 \times 3^2 + 1 \times 3^1 + 2\times 3^0 = 9+3+2=14_{ten}\\ (112_3)^2 = (14)^2_{ten} = 196_{ten}\\ Evaluate \Longrightarrow 400-196 = 204\) Reconvert to base three \(\begin{matrix} 3 & 204\\ 3 & 69 &R0\\ 3 & 22 & R2\\ 3 & 7 & R1\\ 2 & 2 & R1\\ & 0& R2 \uparrow\\ \end{matrix} \\ =21120_3\) |
|
| 2. |
If \(y = 23_{five} + 101_{three}\), find y, leaving your answer in base two A. 1110 B. 10111 C. 11101 D. 111100 Detailed Solution\(23_{five} = X_{ten}; X_{ten} = 2\times 5^1 + 3\times 5^0 = 10 + 3 = 13\\101_{three}=P_{ten}; P_{ten} = 1\times 3^2 + 0\times 3^1 + 1\times 3^0=9+0+1=10_{ten}\\ Y = 13+10=23_{ten}\); Converting to base two \(\begin{matrix} 2 & 23\\ 2 & 11 &R1\\ 2 & 5 & R1\\ 2 & 2 & R1\\ 2 & 1 & R0\\ & 0& R1 \uparrow\\ \end{matrix} \\ =y=10111_2\) |
|
| 3. |
Given that sin (5x - 28)o = cos (3x - 50)o,0 < x < 90o, find the value of x A. 14o B. 21o C. 32o D. 39o Detailed SolutionSin (5x – 28)o = cos (3x - 50)oSince by the trigonometry relation Sin(5x – 28)o = cos[90 – (5x – 28)]o Hence cos(3x – 50)o = cos[90 – (5x – 28)]o 3x – 50 = 90 - (5x-28) 3x – 50 = 90 – 5x + 28 3x + 5x = 90 + 28 + 50 8x = 168 \(x = \frac{168}{8}=21^{\circ}\) |
|
| 4. |
Solve for t in the equation \(\frac{3}{4}t+\frac{1}{3}(21-t)\) = 11, A. \(\frac{9}{13}\) B. \(\frac{9}{5}\) C. 5 D. \(9\frac{3}{5}\) Detailed Solution\(\frac{3}{4}t+\frac{1}{3}(21-t) = 11; \frac{3t}{4} + \frac{7}{1} - \frac{t}{3} = \frac{11}{1}\\\frac{3 \times 3t + 7\times 12 – 4 \times t = 11 \times 12}{12}\\ 9t + 84 – 4t = 132; 5t = 132 – 84\\ 5t = 48; t = \frac{48}{5} = 9\frac{3}{5}\) |
|
| 5. |
A school girl spends \(\frac{1}{4}\) of her pocket money on books and \(\frac{1}{3}\) on dress. What fraction remains? A. \(\frac{5}{6}\) B. \(\frac{7}{12}\) C. \(\frac{5}{12}\) D. \(\frac{1}{6}\) Detailed SolutionLet the girls pocket money be rep. by x. The amount spent on books = \(\frac{1}{4}of\hspace{1mm}x = \frac{x}{4}\)The amount spent on dress \(=\frac{1}{3} of \hspace{1mm}x=\frac{x}{3}\) ∴The fraction that remains = \(\frac{x}{1}-\left(\frac{x}{4}+\frac{x}{3}\right)\\ \frac{3x+4x}{12}; = \frac{12x-7x}{12} = \frac{5x}{12} = \frac{5}{12}\) |
|
| 6. |
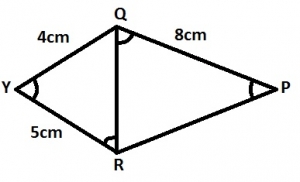 In the diagram, \(R\hat{P}Q = Q\hat{R}Y, \hspace{1mm} P\hat{Q}R = R\hat{Y}Q, \\ \hspace{1mm}|QP| = 3cm \hspace{1mm}|QY| = 4cm \hspace{1mm}and \hspace{1mm}|RY | = 5cm. \hspace{1mm} Find \hspace{1mm}|QR|\) A. 2.0cm B. 2.5cm C. 6.4cm D. 10.0cm Detailed Solution\(\frac{PR}{QR} = \frac{QR}{QY} = \frac{QP}{YR}\) (SSS Congruence)\(\frac{QR}{4} = \frac{8}{5}\) \(QR = \frac{4 \times 8}{5}\) = 6.4 cm |
|
| 7. |
 Find the value of x in the diagram A. 10o B. 28o C. 36o D. 44o Detailed SolutionThe sum of angles at point = 360o(x+10)o + (4x+50)o + 20o + 3xo + 2xo = 360o 10x + 80o = 360o 10x = 360o - 80o = 280o \(\frac{280}{10}=28^{\circ}\) |
|
| 8. |
There are m boys and 12 girls in a class. What is the probability of selecting at random a girl from the class? A. \(\frac{m}{12}\) B. \(\frac{12}{m}\) C. \(\frac{12}{m+12}\) D. \(\frac{12}{m-12}\) Detailed SolutionProb. (a girl) \(=\frac{Number\hspace{1mm} of\hspace{1mm} girls}{Number \hspace{1mm} of \hspace{1mm} boys \hspace{1mm} and \hspace{1mm} girls\hspace{1mm} in \hspace{1mm} class}\\= \frac{12}{m+12}\) |
|
| 9. |
Simplify \(7\frac{1}{2}-\left(2\frac{1}{2}+3\right)\div16\frac{1}{2}\)and correct your answer to the nearest whole number A. 33 B. 8 C. 7 Detailed Solution\(7\frac{1}{2}-\left(2\frac{1}{2}+3\right)\div16\frac{1}{2}; \frac{15}{2} - \left(\frac{5}{2}+\frac{3}{1}\right)\div \frac{33}{2}\\\frac{15}{2} - \left(\frac{5+6}{2}\right)\div \frac{33}{2}; \frac{15}{2} - \frac{11}{2} \div \frac{33}{2}\\ \(\frac{11}{2}\) ÷ \(\frac{33}{2}\) = \(\frac{11}{2}\) * \(\frac{2}{33}\) = \(\frac{11}{33}\) or \(\frac{1}{3}\) (when simplified) \(\frac{15}{2}\) - \(\frac{1}{3}\) = \(\frac{43}{6}\) 7.166 The nearest whole number is 7 |
|
| 10. |
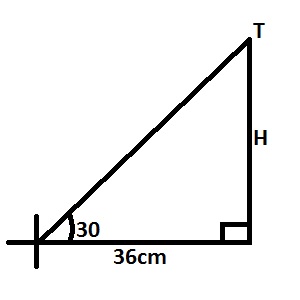
The angle of elevation of the top of a tower from a point on the ground which is 36m away from the foot of the tower is 30o. Calculate the height of the tower. A. 62.35m B. 20.78m C. 18.00m D. 10.39m Detailed Solution
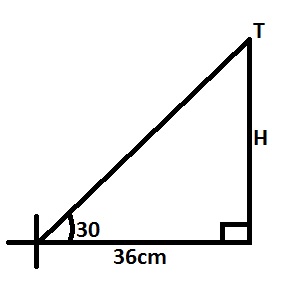 \(Tan 30^{\circ} = \frac{H}{36} \Rightarrow H = 36 \times tan30^{\circ}\\ H = 36 \times 0.5774 = 20.79\) |
| 1. |
1. Evaluate \( 202^2_{three} - 112^2_{three}\) A. 21120 B. 21121 C. 21112 D. 21011 Detailed Solution\(202^2_{three}\)when converted to base ten \(=(202_3)^2\\202_3 = 2 \times 3^2 + 0 \times 3^1 + 2\times 3^0 = 18 + 0 + 2\\ =20_{ten}; (202_3)^2 = (20)^2_{ten} = 400\\ 112^2_{three}\)when converted to base ten \(= (112_3)^2\\ 112_3 = 1 \times 3^2 + 1 \times 3^1 + 2\times 3^0 = 9+3+2=14_{ten}\\ (112_3)^2 = (14)^2_{ten} = 196_{ten}\\ Evaluate \Longrightarrow 400-196 = 204\) Reconvert to base three \(\begin{matrix} 3 & 204\\ 3 & 69 &R0\\ 3 & 22 & R2\\ 3 & 7 & R1\\ 2 & 2 & R1\\ & 0& R2 \uparrow\\ \end{matrix} \\ =21120_3\) |
|
| 2. |
If \(y = 23_{five} + 101_{three}\), find y, leaving your answer in base two A. 1110 B. 10111 C. 11101 D. 111100 Detailed Solution\(23_{five} = X_{ten}; X_{ten} = 2\times 5^1 + 3\times 5^0 = 10 + 3 = 13\\101_{three}=P_{ten}; P_{ten} = 1\times 3^2 + 0\times 3^1 + 1\times 3^0=9+0+1=10_{ten}\\ Y = 13+10=23_{ten}\); Converting to base two \(\begin{matrix} 2 & 23\\ 2 & 11 &R1\\ 2 & 5 & R1\\ 2 & 2 & R1\\ 2 & 1 & R0\\ & 0& R1 \uparrow\\ \end{matrix} \\ =y=10111_2\) |
|
| 3. |
Given that sin (5x - 28)o = cos (3x - 50)o,0 < x < 90o, find the value of x A. 14o B. 21o C. 32o D. 39o Detailed SolutionSin (5x – 28)o = cos (3x - 50)oSince by the trigonometry relation Sin(5x – 28)o = cos[90 – (5x – 28)]o Hence cos(3x – 50)o = cos[90 – (5x – 28)]o 3x – 50 = 90 - (5x-28) 3x – 50 = 90 – 5x + 28 3x + 5x = 90 + 28 + 50 8x = 168 \(x = \frac{168}{8}=21^{\circ}\) |
|
| 4. |
Solve for t in the equation \(\frac{3}{4}t+\frac{1}{3}(21-t)\) = 11, A. \(\frac{9}{13}\) B. \(\frac{9}{5}\) C. 5 D. \(9\frac{3}{5}\) Detailed Solution\(\frac{3}{4}t+\frac{1}{3}(21-t) = 11; \frac{3t}{4} + \frac{7}{1} - \frac{t}{3} = \frac{11}{1}\\\frac{3 \times 3t + 7\times 12 – 4 \times t = 11 \times 12}{12}\\ 9t + 84 – 4t = 132; 5t = 132 – 84\\ 5t = 48; t = \frac{48}{5} = 9\frac{3}{5}\) |
|
| 5. |
A school girl spends \(\frac{1}{4}\) of her pocket money on books and \(\frac{1}{3}\) on dress. What fraction remains? A. \(\frac{5}{6}\) B. \(\frac{7}{12}\) C. \(\frac{5}{12}\) D. \(\frac{1}{6}\) Detailed SolutionLet the girls pocket money be rep. by x. The amount spent on books = \(\frac{1}{4}of\hspace{1mm}x = \frac{x}{4}\)The amount spent on dress \(=\frac{1}{3} of \hspace{1mm}x=\frac{x}{3}\) ∴The fraction that remains = \(\frac{x}{1}-\left(\frac{x}{4}+\frac{x}{3}\right)\\ \frac{3x+4x}{12}; = \frac{12x-7x}{12} = \frac{5x}{12} = \frac{5}{12}\) |
| 6. |
 In the diagram, \(R\hat{P}Q = Q\hat{R}Y, \hspace{1mm} P\hat{Q}R = R\hat{Y}Q, \\ \hspace{1mm}|QP| = 3cm \hspace{1mm}|QY| = 4cm \hspace{1mm}and \hspace{1mm}|RY | = 5cm. \hspace{1mm} Find \hspace{1mm}|QR|\) A. 2.0cm B. 2.5cm C. 6.4cm D. 10.0cm Detailed Solution\(\frac{PR}{QR} = \frac{QR}{QY} = \frac{QP}{YR}\) (SSS Congruence)\(\frac{QR}{4} = \frac{8}{5}\) \(QR = \frac{4 \times 8}{5}\) = 6.4 cm |
|
| 7. |
 Find the value of x in the diagram A. 10o B. 28o C. 36o D. 44o Detailed SolutionThe sum of angles at point = 360o(x+10)o + (4x+50)o + 20o + 3xo + 2xo = 360o 10x + 80o = 360o 10x = 360o - 80o = 280o \(\frac{280}{10}=28^{\circ}\) |
|
| 8. |
There are m boys and 12 girls in a class. What is the probability of selecting at random a girl from the class? A. \(\frac{m}{12}\) B. \(\frac{12}{m}\) C. \(\frac{12}{m+12}\) D. \(\frac{12}{m-12}\) Detailed SolutionProb. (a girl) \(=\frac{Number\hspace{1mm} of\hspace{1mm} girls}{Number \hspace{1mm} of \hspace{1mm} boys \hspace{1mm} and \hspace{1mm} girls\hspace{1mm} in \hspace{1mm} class}\\= \frac{12}{m+12}\) |
|
| 9. |
Simplify \(7\frac{1}{2}-\left(2\frac{1}{2}+3\right)\div16\frac{1}{2}\)and correct your answer to the nearest whole number A. 33 B. 8 C. 7 Detailed Solution\(7\frac{1}{2}-\left(2\frac{1}{2}+3\right)\div16\frac{1}{2}; \frac{15}{2} - \left(\frac{5}{2}+\frac{3}{1}\right)\div \frac{33}{2}\\\frac{15}{2} - \left(\frac{5+6}{2}\right)\div \frac{33}{2}; \frac{15}{2} - \frac{11}{2} \div \frac{33}{2}\\ \(\frac{11}{2}\) ÷ \(\frac{33}{2}\) = \(\frac{11}{2}\) * \(\frac{2}{33}\) = \(\frac{11}{33}\) or \(\frac{1}{3}\) (when simplified) \(\frac{15}{2}\) - \(\frac{1}{3}\) = \(\frac{43}{6}\) 7.166 The nearest whole number is 7 |
|
| 10. |
The angle of elevation of the top of a tower from a point on the ground which is 36m away from the foot of the tower is 30o. Calculate the height of the tower. A. 62.35m B. 20.78m C. 18.00m D. 10.39m Detailed Solution
 \(Tan 30^{\circ} = \frac{H}{36} \Rightarrow H = 36 \times tan30^{\circ}\\ H = 36 \times 0.5774 = 20.79\) |