Year :
2004
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
31 - 40 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
Find the average of the first four prime numbers greater than10 A. 20 B. 19 C. 17 D. 15 Detailed SolutionFirst four prime numbers greater than 10 are 11, 13, 17, 19The average \(= \frac{11+13+17+19}{4}=15\) |
|
| 32. |
Given that \(\sqrt{128}+\sqrt{18}-\sqrt{K} = 7\sqrt{2}\), find K, A. 8 B. 16 C. 32 D. 48 Detailed Solution\(\sqrt{128} +\sqrt{18}-\sqrt{k}=7\sqrt{2}\\\sqrt{2\times 64}+\sqrt{9\times 2} - \sqrt{k} = 7\sqrt{2}\\ 8\sqrt{2} + 3\sqrt{2} - \sqrt{k} = 7\sqrt{2}; 11\sqrt{2} - \sqrt{k} = 7\sqrt{2}\\ -\sqrt{k}=7\sqrt{2}-11\sqrt{2}; -\sqrt{k} = -4\sqrt{2}; \sqrt{k}=4\sqrt{2}\\ =\sqrt{4^2\times 2} = \sqrt{16\times 2}; \sqrt{k}=\sqrt{32}; k = 32\) |
|
| 33. |
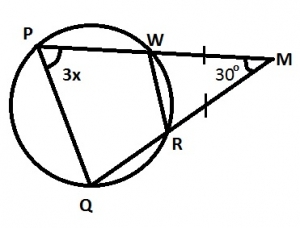 In the diagram, PQRW is a circle. Line P, V and QR are produced to meet at M, where ∠WMR = 30o and |WM| = |MR| Find the value of x A. 10o B. 25o C. 35o D. 60o Detailed SolutionMPQ = PQM = 3x; ∆MPQMPQ + PQM + PMQ = 180o; 3x + 3x + 30o = 180o 6x \times 30o = 180o; 6x + 180o - 30o; 6x + 150o \(x = \frac{150}{6} = 25^{\circ}\) |
|
| 34. |
 The table above gives the marks scored by a group of students in a test Use the table to answer the Question below A. 1 B. 2 C. 3 D. 4 Detailed SolutionMedian = 0, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5Median mark = \(\frac{3+3}{2} = \frac{6}{2} = 3\) |
|
| 35. |
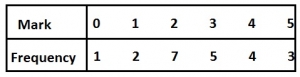 The table above gives the marks scored by a group of students in a test Use the table to answer the Question below A. \(\frac{1}{11}\) B. \(\frac{5}{22}\) C. \(\frac{7}{22}\) D. \(\frac{6}{11}\) Detailed SolutionProb (2 or 3) = prob(2) + prob(3)Prob (mark 2) \(=\frac{7}{22}\) + Prob(mark 3) = \(\frac{5}{22}\) Prob(2 or 3) \(=\frac{7}{22}+\frac{5}{22}=\frac{12}{22}=\frac{6}{11}\) |
|
| 36. |
Find the range of values of x for which\(\frac{x+2}{4}-\frac{x+1}{3}>\frac{1}{2}\) A. x > 4 B. x > -4 C. x < 4 D. x < -4 Detailed Solution\(\frac{x+2}{4}-\frac{x+1}{3}>\frac{1}{2}\\\frac{3(x+2)-4(x+1)>6}{12}; 3x + 6 – 4x – 4 > 6\ -x +2>6; -x > 4; x < -4\) |
|
| 37. |
A boy walks 800m in 20 minutes. Calculate his average speed in km per hour A. 2.4 B. 4 C. 16 D. 24 Detailed Solution\(Average \hspace{1mm}speed = \frac{Distance}{Time\hspace{1mm} taken}\\Distance = 800m = \frac{800}{1000}km = 0.8km\\ Time\hspace{1mm}taken = 20\hspace{1mm}minutes = \frac{20}{60}hr=\frac{1}{3}hr\\Average \hspace{1mm} speed = \left(0.8\div \frac{1}{3}\right)km/hr = (0.8\times3)km/hr\\=2.4km/hr\) |
|
| 38. |
Simplify \(\frac{2}{a+b}-\frac{1}{a-b}\) A. \(\frac{3}{a+b}\) B. \(\frac{a-3b}{a^2-b^2}\) C. \(\frac{3a-b}{a^2 – b^2}\) D. \(\frac{a-3b}{a^2+b^2}\) Detailed SolutionSimplify \(\frac{2}{a+b}-\frac{1}{a-b}; \frac{2(a-b)-1(a+b)}{(a+b)(a-b)}\)= \(\frac{2a-2b-a-b}{(a+b)(a-b)}\) = \(\frac{a-3b}{a^2 - ab + ab - b^2}\) = \(\frac{a-3b}{a^2-b^2}\) |
|
| 39. |
 The diagram is a circle centre O. Find the value of x A. 30o B. 50o C. 61o D. 78o E. 65.5\(^{\circ}\) Detailed Solution∠PQR (Reflex) = 360° – 68° = 292°∠PQR = 2∠PQR 292° = 4x + 30° 4x = 292 – 30 = 262 \(x = \frac{262}{4}=65.5°\) |
|
| 40. |
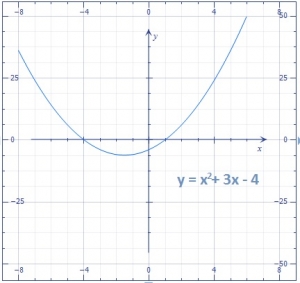 Use the graph to answer the Question below A. 1, 4 B. -1, -4 C. -1, 4 D. -4, 1 Detailed Solutionx2 + 3x – 4 = 0 has roots value at the curve makes touches with the x – axis. The curve contact is at x = -4 and +1. |
| 31. |
Find the average of the first four prime numbers greater than10 A. 20 B. 19 C. 17 D. 15 Detailed SolutionFirst four prime numbers greater than 10 are 11, 13, 17, 19The average \(= \frac{11+13+17+19}{4}=15\) |
|
| 32. |
Given that \(\sqrt{128}+\sqrt{18}-\sqrt{K} = 7\sqrt{2}\), find K, A. 8 B. 16 C. 32 D. 48 Detailed Solution\(\sqrt{128} +\sqrt{18}-\sqrt{k}=7\sqrt{2}\\\sqrt{2\times 64}+\sqrt{9\times 2} - \sqrt{k} = 7\sqrt{2}\\ 8\sqrt{2} + 3\sqrt{2} - \sqrt{k} = 7\sqrt{2}; 11\sqrt{2} - \sqrt{k} = 7\sqrt{2}\\ -\sqrt{k}=7\sqrt{2}-11\sqrt{2}; -\sqrt{k} = -4\sqrt{2}; \sqrt{k}=4\sqrt{2}\\ =\sqrt{4^2\times 2} = \sqrt{16\times 2}; \sqrt{k}=\sqrt{32}; k = 32\) |
|
| 33. |
 In the diagram, PQRW is a circle. Line P, V and QR are produced to meet at M, where ∠WMR = 30o and |WM| = |MR| Find the value of x A. 10o B. 25o C. 35o D. 60o Detailed SolutionMPQ = PQM = 3x; ∆MPQMPQ + PQM + PMQ = 180o; 3x + 3x + 30o = 180o 6x \times 30o = 180o; 6x + 180o - 30o; 6x + 150o \(x = \frac{150}{6} = 25^{\circ}\) |
|
| 34. |
 The table above gives the marks scored by a group of students in a test Use the table to answer the Question below A. 1 B. 2 C. 3 D. 4 Detailed SolutionMedian = 0, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5Median mark = \(\frac{3+3}{2} = \frac{6}{2} = 3\) |
|
| 35. |
 The table above gives the marks scored by a group of students in a test Use the table to answer the Question below A. \(\frac{1}{11}\) B. \(\frac{5}{22}\) C. \(\frac{7}{22}\) D. \(\frac{6}{11}\) Detailed SolutionProb (2 or 3) = prob(2) + prob(3)Prob (mark 2) \(=\frac{7}{22}\) + Prob(mark 3) = \(\frac{5}{22}\) Prob(2 or 3) \(=\frac{7}{22}+\frac{5}{22}=\frac{12}{22}=\frac{6}{11}\) |
| 36. |
Find the range of values of x for which\(\frac{x+2}{4}-\frac{x+1}{3}>\frac{1}{2}\) A. x > 4 B. x > -4 C. x < 4 D. x < -4 Detailed Solution\(\frac{x+2}{4}-\frac{x+1}{3}>\frac{1}{2}\\\frac{3(x+2)-4(x+1)>6}{12}; 3x + 6 – 4x – 4 > 6\ -x +2>6; -x > 4; x < -4\) |
|
| 37. |
A boy walks 800m in 20 minutes. Calculate his average speed in km per hour A. 2.4 B. 4 C. 16 D. 24 Detailed Solution\(Average \hspace{1mm}speed = \frac{Distance}{Time\hspace{1mm} taken}\\Distance = 800m = \frac{800}{1000}km = 0.8km\\ Time\hspace{1mm}taken = 20\hspace{1mm}minutes = \frac{20}{60}hr=\frac{1}{3}hr\\Average \hspace{1mm} speed = \left(0.8\div \frac{1}{3}\right)km/hr = (0.8\times3)km/hr\\=2.4km/hr\) |
|
| 38. |
Simplify \(\frac{2}{a+b}-\frac{1}{a-b}\) A. \(\frac{3}{a+b}\) B. \(\frac{a-3b}{a^2-b^2}\) C. \(\frac{3a-b}{a^2 – b^2}\) D. \(\frac{a-3b}{a^2+b^2}\) Detailed SolutionSimplify \(\frac{2}{a+b}-\frac{1}{a-b}; \frac{2(a-b)-1(a+b)}{(a+b)(a-b)}\)= \(\frac{2a-2b-a-b}{(a+b)(a-b)}\) = \(\frac{a-3b}{a^2 - ab + ab - b^2}\) = \(\frac{a-3b}{a^2-b^2}\) |
|
| 39. |
 The diagram is a circle centre O. Find the value of x A. 30o B. 50o C. 61o D. 78o E. 65.5\(^{\circ}\) Detailed Solution∠PQR (Reflex) = 360° – 68° = 292°∠PQR = 2∠PQR 292° = 4x + 30° 4x = 292 – 30 = 262 \(x = \frac{262}{4}=65.5°\) |
|
| 40. |
 Use the graph to answer the Question below A. 1, 4 B. -1, -4 C. -1, 4 D. -4, 1 Detailed Solutionx2 + 3x – 4 = 0 has roots value at the curve makes touches with the x – axis. The curve contact is at x = -4 and +1. |