Year :
2007
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
1 - 10 of 47 Questions
| # | Question | Ans |
|---|---|---|
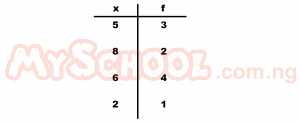
| 1. |
If 5, 8, 6 and 2 occur with frequencies 3, 2, 4 and 1 respectively. Find the product of the modal and the median number A. 36 B. 48 C. 30 D. 40 Detailed Solution
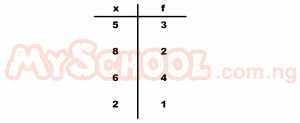 2, 5, 5, 6, 6, ,6, 6, 8, 8 Position of median = N/2 = 8/2 = 4th and 5th ∴Median = (6+6) / 2 = 12/2 = 6 Mode the item that repeat itself most = 6 ∴Product of modal and median number = 6 x 6 = 36 |
|
| 2. |
In a basket, there are 6 grapes, 11 bananas and 13 oranges. If one fruit is chosen at random. What is the probability that the fruit is either a grape or a banana A. 6/30 B. 5/30 C. 17/30 D. 11/30 Detailed SolutionNumber of grapes = 6Number of banana = 11 Number of oranges = 13 Total = 30 P(Grape) = 6/30, P(Banana) = 11/30 P(Orange) = 13/30 ∴P(Either grape or banana) = 6/30 + 11/30 = 17/30 |
|
| 3. |
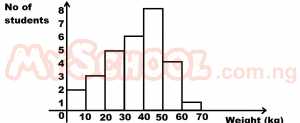 The histogram above represents the weights of students who traveled out to their school for an examination. How many people made the trip? A. 78 B. 38 C. 29 D. 69 Detailed Solution
|
|
| 4. |
A senatorial candidate had planned to visit seven cities prior to a primary election. However, he could only visit four of the cities. How many different itineraries could be considered? A. 640 B. 840 C. 520 D. 920 Detailed SolutionNumber of itineraries = 7P4=\(\frac{7!}{(7-4)!}\\ =\frac{7!}{3!}\\ =\frac{7 \times 6 \times 5 \times 4 \times 3!}{3!}\\ =840\) |
|
| 5. |
 The pie chart above illustrate the amount of private time a student spends in a week studying various subjects. Find the value of k A. 90o B. 60o C. 30o D. 40o Detailed SolutionK + 5K + 3K + 75 + 105 = 360 (at a point)6K + 180 = 360 6K = 360 - 180 6K = 180 k = 180/6 = 30o |
|
| 6. |
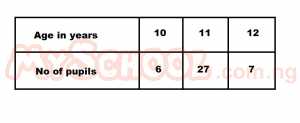 The table above shows the number of pupils in each age group in a class. What is the probability that a pupil chosen at random is at least 11 years old? A. 27/40 B. 17/20 C. 3/30 D. 33/40 Detailed SolutionP(At least 11 yrs) = P(11yrs) + P(12yrs)= 27/40 + 7/40 = 34/40 = 17/20 |
|
| 7. |
What is the mean deviation of 3, 5, 8, 11, 12 and 21? A. 4.7 B. 60 C. 3.7 D. 10 Detailed Solution
 mean deviation \(= \frac{\sum|x-\bar{x}|}{n} = \frac{28}{6}\) = 4.7 |
|
| 8. |
 Table:The table above gives the frequency distribution of marks obtained by a group of students in a test. If the total mark scored is 200, calculate the value of y A. 15 B. 13 C. 11 D. 8 Detailed SolutionTotal mark scored = 200∴200 = 15 + 4y - 4 + 5y + 54 + 28 + 8 200 = 9y + 101 200 - 101 = 9y 99 = 9y ∴y = 11 |
|
| 9. |
In how many ways can 6 subjects be selected from 10 subjects for an examination A. 218 B. 216 C. 215 D. 210 Detailed Solution\(^{10}C_6 = \frac{10!}{(10-6)!6!}=\frac{10!}{4!6!}\\=\frac{(10\times 9\times 8\times 7 \times 6!)}{4\times 3\times 2\times 1\times 6!}\\ =210\) |
|
| 10. |
Integrate \(\frac{x^2 -\sqrt{x}}{x}\) with respect to x A. \(\frac{x^2}{2}-2\sqrt{x}+K\) B. \(\frac{2(x^2 - x)}{3x}+K\) C. \(\frac{x^2}{2}-\sqrt{x}+K\) D. \(\frac{(x^2 - x)}{3x}+K\) Detailed Solution\(\int \frac{x^2 -\sqrt{x}}{x} = \int \frac{x^2}{x} - \frac{x^{\frac{1}{2}}}{x}\\\int x - x^{\frac{-1}{2}}\\ =\left(\frac{1}{2}\right)x^2 - \frac{x^{\frac{1}{2}}}{\frac{1}{2}}+K\\ =\frac{x^2}{2}-2x^{\frac{1}{2}}+K\\ =\frac{x^2}{2}-2\sqrt{x}+K\) |
| 1. |
If 5, 8, 6 and 2 occur with frequencies 3, 2, 4 and 1 respectively. Find the product of the modal and the median number A. 36 B. 48 C. 30 D. 40 Detailed Solution
 2, 5, 5, 6, 6, ,6, 6, 8, 8 Position of median = N/2 = 8/2 = 4th and 5th ∴Median = (6+6) / 2 = 12/2 = 6 Mode the item that repeat itself most = 6 ∴Product of modal and median number = 6 x 6 = 36 |
|
| 2. |
In a basket, there are 6 grapes, 11 bananas and 13 oranges. If one fruit is chosen at random. What is the probability that the fruit is either a grape or a banana A. 6/30 B. 5/30 C. 17/30 D. 11/30 Detailed SolutionNumber of grapes = 6Number of banana = 11 Number of oranges = 13 Total = 30 P(Grape) = 6/30, P(Banana) = 11/30 P(Orange) = 13/30 ∴P(Either grape or banana) = 6/30 + 11/30 = 17/30 |
|
| 3. |
 The histogram above represents the weights of students who traveled out to their school for an examination. How many people made the trip? A. 78 B. 38 C. 29 D. 69 Detailed Solution
|
|
| 4. |
A senatorial candidate had planned to visit seven cities prior to a primary election. However, he could only visit four of the cities. How many different itineraries could be considered? A. 640 B. 840 C. 520 D. 920 Detailed SolutionNumber of itineraries = 7P4=\(\frac{7!}{(7-4)!}\\ =\frac{7!}{3!}\\ =\frac{7 \times 6 \times 5 \times 4 \times 3!}{3!}\\ =840\) |
|
| 5. |
 The pie chart above illustrate the amount of private time a student spends in a week studying various subjects. Find the value of k A. 90o B. 60o C. 30o D. 40o Detailed SolutionK + 5K + 3K + 75 + 105 = 360 (at a point)6K + 180 = 360 6K = 360 - 180 6K = 180 k = 180/6 = 30o |
| 6. |
 The table above shows the number of pupils in each age group in a class. What is the probability that a pupil chosen at random is at least 11 years old? A. 27/40 B. 17/20 C. 3/30 D. 33/40 Detailed SolutionP(At least 11 yrs) = P(11yrs) + P(12yrs)= 27/40 + 7/40 = 34/40 = 17/20 |
|
| 7. |
What is the mean deviation of 3, 5, 8, 11, 12 and 21? A. 4.7 B. 60 C. 3.7 D. 10 Detailed Solution
 mean deviation \(= \frac{\sum|x-\bar{x}|}{n} = \frac{28}{6}\) = 4.7 |
|
| 8. |
 Table:The table above gives the frequency distribution of marks obtained by a group of students in a test. If the total mark scored is 200, calculate the value of y A. 15 B. 13 C. 11 D. 8 Detailed SolutionTotal mark scored = 200∴200 = 15 + 4y - 4 + 5y + 54 + 28 + 8 200 = 9y + 101 200 - 101 = 9y 99 = 9y ∴y = 11 |
|
| 9. |
In how many ways can 6 subjects be selected from 10 subjects for an examination A. 218 B. 216 C. 215 D. 210 Detailed Solution\(^{10}C_6 = \frac{10!}{(10-6)!6!}=\frac{10!}{4!6!}\\=\frac{(10\times 9\times 8\times 7 \times 6!)}{4\times 3\times 2\times 1\times 6!}\\ =210\) |
|
| 10. |
Integrate \(\frac{x^2 -\sqrt{x}}{x}\) with respect to x A. \(\frac{x^2}{2}-2\sqrt{x}+K\) B. \(\frac{2(x^2 - x)}{3x}+K\) C. \(\frac{x^2}{2}-\sqrt{x}+K\) D. \(\frac{(x^2 - x)}{3x}+K\) Detailed Solution\(\int \frac{x^2 -\sqrt{x}}{x} = \int \frac{x^2}{x} - \frac{x^{\frac{1}{2}}}{x}\\\int x - x^{\frac{-1}{2}}\\ =\left(\frac{1}{2}\right)x^2 - \frac{x^{\frac{1}{2}}}{\frac{1}{2}}+K\\ =\frac{x^2}{2}-2x^{\frac{1}{2}}+K\\ =\frac{x^2}{2}-2\sqrt{x}+K\) |