Year :
2007
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
11 - 20 of 47 Questions
| # | Question | Ans |
|---|---|---|
| 11. |
If y = x cos x, find dy/dx A. sin x - x cos x B. sin x + x cos x C. cos x + x sin x D. cos x - x sin x Detailed Solutiony = x cos xdy/dx = 1. cos x + x (-sin x) = cos x - x sin x |
|
| 12. |
Find the value of x for which the function f(x) = 2x3 - x2 - 4x + 4 has a maximum value A. 2/3 B. 1 C. - 2/3 D. - 1 Detailed Solutionf(x) = 2x3 - x2 - 4x – 4f’(x) = 6x2 - 2x – 4 As f’(x) = 0 Implies 6x2 - 2x – 4 = 0 3x – x – 2 = 0 (By dividing by 2) (3x – 2)(x + 1) = 0 3x – 2 = 0 implies x = -2/3 Or x + 1 = 0 implies x = -1 f’(x) = 6x2 - 2x – 4 f’’(x) = 12x – 2 At max point f’’(x) < 0 ∴f’’(x) = 12x – 2 at x = -1 = 12(-1) – 2 = -12 – 2 = -14 ∴Max at x = 1 |
|
| 13. |
Determine the value of \(\int_0 ^{\frac{\pi}{2} A. -2 B. -1/2 C. -3 D. -3/2 Detailed Solution\(\int_0 ^{\frac{\pi}{2}}(-2cos x)dx = [-2sin x + c]_0 ^{\frac{\pi}{2}}\\=(-2sin\frac{\pi}{2}+c+2sin0-c)\\ =-2sin90+c+2sin0-c\\ =-2(1)+2(0)\\ =-2\) |
|
| 14. |
A binary operation ⊕ on real numbers is defined by x⊕y = xy + x + y for any two real numbers x and y. The value of (-3/4)⊕6 is A. 3/4 B. -9/2 C. 45/4 D. -3/4 Detailed Solutionx⊕y = xy + x + y= -3/4 (6) + (-3/4) + 6 = -9/2 - 3/4 + 6 = (-18-3+3+24) / 4 = 3/4 |
|
| 15. |
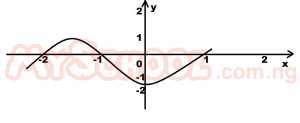 The graph above is represented by A. y = x3 - 3x - 2 B. y = x3 + 2x2 - x - 2 C. y = x3 - 4x2 + 5x - 2 D. y = x3 - 4x + 2 Detailed Solutionx = -2, x = -1 and x = 1then the factors; x+2, x+1 and x-1 Product of the factors; (x+2)(x+1)(x-1) = y = (x + 2)(x2 - x + x - 1) = y = (x+2)(x2-1) x3 - x + 2x2 - 2 = y x3 + 2x2 - x - 2 = y |
|
| 16. |
Make L the subjects of the formula if \(\sqrt{\frac{42w}{5l}}\) A. \(\sqrt{\frac{42w}{5d}}\) B. \(\frac{42W}{5d^2}\) C. \(\frac{42}{5dW}\) D. \(\frac{1}{d}\sqrt{\frac{42w}{5}}\) Detailed Solution\(\sqrt{\frac{42w}{5l}}\)square both side of the equation \(d^2 = \left(\sqrt{\frac{42W}{5l}}\right)^2\\ d^2 = \frac{42W}{5l}\\ 5ld^2=42W\\ l = \frac{42W}{5d^2}\) |
|
| 17. |
The solution of the quadratic inequality (x3 + x - 12) ≥ 0 is A. x ≥ -3 or x ≤ 4 B. x ≥ 3 or x ≥ -4 C. x ≤ 3 or x v -4 D. x ≥ 3 or x ≤ -4 Detailed Solution(x3 + x - 12) ≥ 0(x + 4)(x - 3) ≥ 0 Either x + 4 ≥ 0 implies x ≥ -4 Or x - 3 ≥ 0 implies x ≥ 3 ∴ x ≥ 3 or x ≥ -4 |
|
| 18. |
Factorize 2t2 + t - 15 A. (2t - 3)(t + 5) B. (t + 3)(2t - 5) C. (t + 3)(t - 5) D. (2t + 3)(t - 5) Detailed Solution2t2 + t - 15 = (2t-5)(t+3) |
|
| 19. |
Solve the inequalities -3(x - 2) < -2(x + 3) A. x > 12 B. x < 12 C. x > -12 D. x < - 12 Detailed Solution-3(x-3) < -2(x+3) = -3x + 6 < -2x - 6-3x + 2x < -6 - 6 -x < - 12 x > -12/-1 x > 12 |
|
| 20. |
W ∝ L2 and W = 6 when L = 4. If L = √17 find W A. 67/8 B. 65/8 C. 63/8 D. 61/8 Detailed SolutionW ∝ L2W = KL2 K = W/L2 K = 6/42 K = 6/16 = 3/8 W = 3/8 L2 W = 3/8(√17)2 W = 3/8 x 17 W = 51/8 = 63/8 |
| 11. |
If y = x cos x, find dy/dx A. sin x - x cos x B. sin x + x cos x C. cos x + x sin x D. cos x - x sin x Detailed Solutiony = x cos xdy/dx = 1. cos x + x (-sin x) = cos x - x sin x |
|
| 12. |
Find the value of x for which the function f(x) = 2x3 - x2 - 4x + 4 has a maximum value A. 2/3 B. 1 C. - 2/3 D. - 1 Detailed Solutionf(x) = 2x3 - x2 - 4x – 4f’(x) = 6x2 - 2x – 4 As f’(x) = 0 Implies 6x2 - 2x – 4 = 0 3x – x – 2 = 0 (By dividing by 2) (3x – 2)(x + 1) = 0 3x – 2 = 0 implies x = -2/3 Or x + 1 = 0 implies x = -1 f’(x) = 6x2 - 2x – 4 f’’(x) = 12x – 2 At max point f’’(x) < 0 ∴f’’(x) = 12x – 2 at x = -1 = 12(-1) – 2 = -12 – 2 = -14 ∴Max at x = 1 |
|
| 13. |
Determine the value of \(\int_0 ^{\frac{\pi}{2} A. -2 B. -1/2 C. -3 D. -3/2 Detailed Solution\(\int_0 ^{\frac{\pi}{2}}(-2cos x)dx = [-2sin x + c]_0 ^{\frac{\pi}{2}}\\=(-2sin\frac{\pi}{2}+c+2sin0-c)\\ =-2sin90+c+2sin0-c\\ =-2(1)+2(0)\\ =-2\) |
|
| 14. |
A binary operation ⊕ on real numbers is defined by x⊕y = xy + x + y for any two real numbers x and y. The value of (-3/4)⊕6 is A. 3/4 B. -9/2 C. 45/4 D. -3/4 Detailed Solutionx⊕y = xy + x + y= -3/4 (6) + (-3/4) + 6 = -9/2 - 3/4 + 6 = (-18-3+3+24) / 4 = 3/4 |
|
| 15. |
 The graph above is represented by A. y = x3 - 3x - 2 B. y = x3 + 2x2 - x - 2 C. y = x3 - 4x2 + 5x - 2 D. y = x3 - 4x + 2 Detailed Solutionx = -2, x = -1 and x = 1then the factors; x+2, x+1 and x-1 Product of the factors; (x+2)(x+1)(x-1) = y = (x + 2)(x2 - x + x - 1) = y = (x+2)(x2-1) x3 - x + 2x2 - 2 = y x3 + 2x2 - x - 2 = y |
| 16. |
Make L the subjects of the formula if \(\sqrt{\frac{42w}{5l}}\) A. \(\sqrt{\frac{42w}{5d}}\) B. \(\frac{42W}{5d^2}\) C. \(\frac{42}{5dW}\) D. \(\frac{1}{d}\sqrt{\frac{42w}{5}}\) Detailed Solution\(\sqrt{\frac{42w}{5l}}\)square both side of the equation \(d^2 = \left(\sqrt{\frac{42W}{5l}}\right)^2\\ d^2 = \frac{42W}{5l}\\ 5ld^2=42W\\ l = \frac{42W}{5d^2}\) |
|
| 17. |
The solution of the quadratic inequality (x3 + x - 12) ≥ 0 is A. x ≥ -3 or x ≤ 4 B. x ≥ 3 or x ≥ -4 C. x ≤ 3 or x v -4 D. x ≥ 3 or x ≤ -4 Detailed Solution(x3 + x - 12) ≥ 0(x + 4)(x - 3) ≥ 0 Either x + 4 ≥ 0 implies x ≥ -4 Or x - 3 ≥ 0 implies x ≥ 3 ∴ x ≥ 3 or x ≥ -4 |
|
| 18. |
Factorize 2t2 + t - 15 A. (2t - 3)(t + 5) B. (t + 3)(2t - 5) C. (t + 3)(t - 5) D. (2t + 3)(t - 5) Detailed Solution2t2 + t - 15 = (2t-5)(t+3) |
|
| 19. |
Solve the inequalities -3(x - 2) < -2(x + 3) A. x > 12 B. x < 12 C. x > -12 D. x < - 12 Detailed Solution-3(x-3) < -2(x+3) = -3x + 6 < -2x - 6-3x + 2x < -6 - 6 -x < - 12 x > -12/-1 x > 12 |
|
| 20. |
W ∝ L2 and W = 6 when L = 4. If L = √17 find W A. 67/8 B. 65/8 C. 63/8 D. 61/8 Detailed SolutionW ∝ L2W = KL2 K = W/L2 K = 6/42 K = 6/16 = 3/8 W = 3/8 L2 W = 3/8(√17)2 W = 3/8 x 17 W = 51/8 = 63/8 |