Year : 
2007
Title : 
Mathematics (Core)
Exam : 
JAMB Exam

Paper 1 | Objectives

31 - 40 of 47 Questions

# Question Ans
31.

Given
P = {1, 3, 5, 7, 9, 11}
and Q = {2, 4, 6, 8, 10, 12}. Determine the relationship between P and Q

A. P∩Q = ∅

B. P ⊂ Q

C. Q⊂P

D. P = Q

Detailed Solution

P = {1, 3, 5, 7, 9, 11}
Q = {2, 4, 6, 8, 1, 12}
P∩Q = {1, 3, 5, 7, 9, 11}∩{2, 4, 6, 8, 1, 12}
= {} = ∅
32.

Evaluate 101122 - 10122

A. 1100002

B. 1102

C. 11000002

D. 110002

Detailed Solution

101122 - 10122 = (1x23 + 0x22 + 1x21 + 1x20)2 - (1x22 + 0x21 + 1x22)2
(1x8 + 0x4 + 1x2 + 1x1) 2 - (1x4 + 0x2 + 1x1) 2)
= (8 + 0 + 2 + 1) 2 - (4 + 0 + 1) 2
= 112 - 52
= 16 x 6 = 96
9610 to base 2
2/96 = 48 R 0
2/48 =
33.

If X = {all the perfect squares less than 40}
Y = {all the odd numbers fro, 1 to 15}. Find X ∩ Y.

A. {3, 9}

B. {9}

C. {9, 25}

D. {1, 9}

Detailed Solution

All the perfect squares < 40
X = {1, 4, 9, 16, 25, 36}
All the odd numbers from 1 to 15
Y = {1, 3, 5, 7, 9, 11, 13, 15}
X ∩ Y = {1, 9}
34.

Calculate the length of an arc of a circle diameter 14 cm, which substends an angle of 90o at the center of the circle

A. 7π/2 cm

B. 7π cm

C. 14π cm

D. 7π/4 cm

Detailed Solution

Length of an arc = θ/360 x 2πr
90/360 x 2 x π x 7
= 7π/2
35.

If the lines 3y = 4x - 1 and qy = x + 3 are parallel to each other, the value of q is

A. -4/3

B. -3/4

C. 4/3

D. 3/4

Detailed Solution

If the line 3y = 4x – 1 is parallel t[ line qy = x + 3
Implies gradient of 3y = 4x – 1
Y = 4/3x - 1/3
∴Gradient = 4/3
Gradient of line qy = x + 3
Y = 1/qx + 3/q
∴ Gradient = 1/q
4/3 = 1/q
4q = 3
Q = 3/4
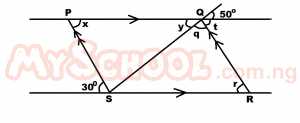
36.

In the parallelogram PQRS above, find angle SQR

A. 100o

B. 80o

C. 50o

D. 30o

Detailed Solution

x = 30o (alternate ∠s b/c PQ//Sr)
Y = 50o (vertical opposite ∠s)
r = 30o (alternate ∠s b/c PQ//SR)
But = y + q + t = 180o (∠s on a straight line)
50 + q + 30 = 180
q + 80 = 180
q = 180 -80
q = 100o
37.

The volume of a hemispherical bowl is \(718\frac{2}{3}\). Find its radius .

A. 4.0 cm

B. 5.6 cm

C. 7.0 cm

D. 3.8 cm

Detailed Solution

Volume of bowl \(\frac{2}{3}\pi r^2\\
718\frac{2}{3}=\frac{2}{3}\pi r^2\\
\frac{2156}{3}=\frac{2}{3} \times \frac{22}{7} \times r^3
∴r^3 = \frac{2156 \times 3 \times 7}{3 \times 2 \times 22}\\
r^3 = 343\\
r = \sqrt[3]{343}\\
r= 7.0cm\)
38.

A particle P moves between points S and T such that angles SPT is always constant of ST constant. Find the locus of P

A. It is a semi circle with ST as diameter

B. It is a perpendicular bisector of St

C. It is a quadrant of a circle with ST as diameter

D. It is a straight line perpendicular to ST

A
39.

If the lines 2y - kx + 2 = 0 and y + x - k/2 = 0 Intersect at (1, -2), find the value of k

A. -4

B. -3

C. -2

D. -1

Detailed Solution

If the point of intersection is (1, -2), it implies that x = 1 and y = -2 when the two equation are solved simultaneously.
∴ substitute x = 1 and y = -2 in any of the equations
2y - k x + 2 = 0
2(-2) - k(1) + 2 = 0
-4 - k + 2 = 0
-4 + 2 = k
-2 = k
40.

A man 40 m from the foot of a tower observes the angle of elevation of the tower to be 30o. Determine the height of the tower.

A. \(\frac{40\sqrt{3}}{3}m\)

B. 20 m

C. 40√3 m

D. 40 m

Detailed Solution

\(Tan 30 = \frac{h}{40}\\
\frac{1}{\sqrt{3}}=\frac{h}{40}\\
h\sqrt{3}=40\\
h = \frac{40}{\sqrt{3}}\\
h = \frac{40}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\\
h = \frac{40\sqrt{3}}{3}\)
31.

Given
P = {1, 3, 5, 7, 9, 11}
and Q = {2, 4, 6, 8, 10, 12}. Determine the relationship between P and Q

A. P∩Q = ∅

B. P ⊂ Q

C. Q⊂P

D. P = Q

Detailed Solution

P = {1, 3, 5, 7, 9, 11}
Q = {2, 4, 6, 8, 1, 12}
P∩Q = {1, 3, 5, 7, 9, 11}∩{2, 4, 6, 8, 1, 12}
= {} = ∅
32.

Evaluate 101122 - 10122

A. 1100002

B. 1102

C. 11000002

D. 110002

Detailed Solution

101122 - 10122 = (1x23 + 0x22 + 1x21 + 1x20)2 - (1x22 + 0x21 + 1x22)2
(1x8 + 0x4 + 1x2 + 1x1) 2 - (1x4 + 0x2 + 1x1) 2)
= (8 + 0 + 2 + 1) 2 - (4 + 0 + 1) 2
= 112 - 52
= 16 x 6 = 96
9610 to base 2
2/96 = 48 R 0
2/48 =
33.

If X = {all the perfect squares less than 40}
Y = {all the odd numbers fro, 1 to 15}. Find X ∩ Y.

A. {3, 9}

B. {9}

C. {9, 25}

D. {1, 9}

Detailed Solution

All the perfect squares < 40
X = {1, 4, 9, 16, 25, 36}
All the odd numbers from 1 to 15
Y = {1, 3, 5, 7, 9, 11, 13, 15}
X ∩ Y = {1, 9}
34.

Calculate the length of an arc of a circle diameter 14 cm, which substends an angle of 90o at the center of the circle

A. 7π/2 cm

B. 7π cm

C. 14π cm

D. 7π/4 cm

Detailed Solution

Length of an arc = θ/360 x 2πr
90/360 x 2 x π x 7
= 7π/2
35.

If the lines 3y = 4x - 1 and qy = x + 3 are parallel to each other, the value of q is

A. -4/3

B. -3/4

C. 4/3

D. 3/4

Detailed Solution

If the line 3y = 4x – 1 is parallel t[ line qy = x + 3
Implies gradient of 3y = 4x – 1
Y = 4/3x - 1/3
∴Gradient = 4/3
Gradient of line qy = x + 3
Y = 1/qx + 3/q
∴ Gradient = 1/q
4/3 = 1/q
4q = 3
Q = 3/4
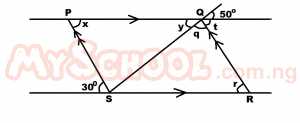
36.

In the parallelogram PQRS above, find angle SQR

A. 100o

B. 80o

C. 50o

D. 30o

Detailed Solution

x = 30o (alternate ∠s b/c PQ//Sr)
Y = 50o (vertical opposite ∠s)
r = 30o (alternate ∠s b/c PQ//SR)
But = y + q + t = 180o (∠s on a straight line)
50 + q + 30 = 180
q + 80 = 180
q = 180 -80
q = 100o
37.

The volume of a hemispherical bowl is \(718\frac{2}{3}\). Find its radius .

A. 4.0 cm

B. 5.6 cm

C. 7.0 cm

D. 3.8 cm

Detailed Solution

Volume of bowl \(\frac{2}{3}\pi r^2\\
718\frac{2}{3}=\frac{2}{3}\pi r^2\\
\frac{2156}{3}=\frac{2}{3} \times \frac{22}{7} \times r^3
∴r^3 = \frac{2156 \times 3 \times 7}{3 \times 2 \times 22}\\
r^3 = 343\\
r = \sqrt[3]{343}\\
r= 7.0cm\)
38.

A particle P moves between points S and T such that angles SPT is always constant of ST constant. Find the locus of P

A. It is a semi circle with ST as diameter

B. It is a perpendicular bisector of St

C. It is a quadrant of a circle with ST as diameter

D. It is a straight line perpendicular to ST

A
39.

If the lines 2y - kx + 2 = 0 and y + x - k/2 = 0 Intersect at (1, -2), find the value of k

A. -4

B. -3

C. -2

D. -1

Detailed Solution

If the point of intersection is (1, -2), it implies that x = 1 and y = -2 when the two equation are solved simultaneously.
∴ substitute x = 1 and y = -2 in any of the equations
2y - k x + 2 = 0
2(-2) - k(1) + 2 = 0
-4 - k + 2 = 0
-4 + 2 = k
-2 = k
40.

A man 40 m from the foot of a tower observes the angle of elevation of the tower to be 30o. Determine the height of the tower.

A. \(\frac{40\sqrt{3}}{3}m\)

B. 20 m

C. 40√3 m

D. 40 m

Detailed Solution

\(Tan 30 = \frac{h}{40}\\
\frac{1}{\sqrt{3}}=\frac{h}{40}\\
h\sqrt{3}=40\\
h = \frac{40}{\sqrt{3}}\\
h = \frac{40}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\\
h = \frac{40\sqrt{3}}{3}\)