Year :
2007
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 47 of 47 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
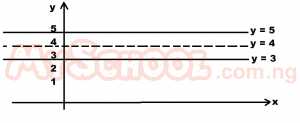
Find the locus of point equidistant from two straight lines y - 5 = 0 and y - 3 = 0 A. y - 2 = 0 B. y - 4 = 0 C. y - 1 = 0 D. y - 3 = 0 Detailed Solution
 |
|
| 42. |
What is the value of k if the mid-point of the line joining (1 - k, - 4) and (2, k + 1) is (-k , k)? A. -3 B. -1 C. -4 D. -2 Detailed Solution(1-k+2) / 2 = - k and -4 + k + 1 = k3-k = -2k and -3 + k = 2k K = -3 and k = -3 |
|
| 43. |
Find the size of each exterior angle of a regular octagon A. 51o B. 45o C. 40o D. 36o Detailed SolutionEach Exterior ∠ = 360/n= 360/8 = 45o |
|
| 44. |
Find the value of \(\frac{tan 60^o - tan 30^o}{tan 60^o + tan 30^o}\) A. \(\frac{4}{\sqrt{3}}\) B. \(\frac{2}{\sqrt{3}}\) C. 1 D. \(\frac{1}{2}\) Detailed Solution\(\frac{tan 60^o - tan 30^o}{tan 60^o + tan 30^o}= \frac{\sqrt{3}-\frac{1}{\sqrt{3}}}{\sqrt{3}+\frac{1}{\sqrt{3}}}\\=\left(\frac{\sqrt{3}\sqrt{3}-1}{\sqrt{3}}\right)\div \left(\frac{\sqrt{3}\sqrt{3}+1}{\sqrt{3}}\right)\\ =\frac{(3-1)}{(3+1)}\\ =\frac{2}{4}=\frac{1}{2}\) |
|
| 45. |
The area of a square is 144 sqcm. Find the length of the diagonal. A. 13 cm B. 12√2 cm C. 12 cm D. 11√3 cm Detailed Solution
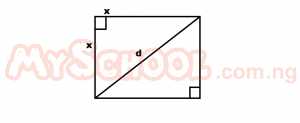 144 = x2 √144 = x 12 = x But d2 = 122 x 122 = 144 + 144 = 288 d = √288 = √144 x 2 = 12√2 |
|
| 46. |
If y = (1 + x)2, find \(\frac{dy}{dx}\) A. x - 1 B. 2 + 2x C. 1 + 2x D. 2x - 1 Detailed SolutionIf y = (1 + x)2, find \(\frac{dy}{dx}\)y = (1 + x)2 \(\frac{dy}{dx}\) = 2(1 + x) = 2 + 2x |
|
| 47. |
The sum of the ages of Musa and Lawal is 28 years. After sharing a certain sum of money in the ratio of their ages, Musa gets N600 and Lawal N800. How old is Lawal? A. 14 years B. 20 years C. 12 years D. 16 years Detailed SolutionM + L = 28,M : L = 600 : 800 = 3 : 4 \(\frac{M}{L}\) = \(\frac{3}{4}\) \(\to\) M = \(\frac{3}{4}\)L \(\frac{3}{4}\)L + L = 28 \(\frac{7L}{4}\) = 28 L = \(\frac{4 \times 28}{7}\) = 16 |
| 41. |
Find the locus of point equidistant from two straight lines y - 5 = 0 and y - 3 = 0 A. y - 2 = 0 B. y - 4 = 0 C. y - 1 = 0 D. y - 3 = 0 Detailed Solution
 |
|
| 42. |
What is the value of k if the mid-point of the line joining (1 - k, - 4) and (2, k + 1) is (-k , k)? A. -3 B. -1 C. -4 D. -2 Detailed Solution(1-k+2) / 2 = - k and -4 + k + 1 = k3-k = -2k and -3 + k = 2k K = -3 and k = -3 |
|
| 43. |
Find the size of each exterior angle of a regular octagon A. 51o B. 45o C. 40o D. 36o Detailed SolutionEach Exterior ∠ = 360/n= 360/8 = 45o |
|
| 44. |
Find the value of \(\frac{tan 60^o - tan 30^o}{tan 60^o + tan 30^o}\) A. \(\frac{4}{\sqrt{3}}\) B. \(\frac{2}{\sqrt{3}}\) C. 1 D. \(\frac{1}{2}\) Detailed Solution\(\frac{tan 60^o - tan 30^o}{tan 60^o + tan 30^o}= \frac{\sqrt{3}-\frac{1}{\sqrt{3}}}{\sqrt{3}+\frac{1}{\sqrt{3}}}\\=\left(\frac{\sqrt{3}\sqrt{3}-1}{\sqrt{3}}\right)\div \left(\frac{\sqrt{3}\sqrt{3}+1}{\sqrt{3}}\right)\\ =\frac{(3-1)}{(3+1)}\\ =\frac{2}{4}=\frac{1}{2}\) |
| 45. |
The area of a square is 144 sqcm. Find the length of the diagonal. A. 13 cm B. 12√2 cm C. 12 cm D. 11√3 cm Detailed Solution
 144 = x2 √144 = x 12 = x But d2 = 122 x 122 = 144 + 144 = 288 d = √288 = √144 x 2 = 12√2 |
|
| 46. |
If y = (1 + x)2, find \(\frac{dy}{dx}\) A. x - 1 B. 2 + 2x C. 1 + 2x D. 2x - 1 Detailed SolutionIf y = (1 + x)2, find \(\frac{dy}{dx}\)y = (1 + x)2 \(\frac{dy}{dx}\) = 2(1 + x) = 2 + 2x |
|
| 47. |
The sum of the ages of Musa and Lawal is 28 years. After sharing a certain sum of money in the ratio of their ages, Musa gets N600 and Lawal N800. How old is Lawal? A. 14 years B. 20 years C. 12 years D. 16 years Detailed SolutionM + L = 28,M : L = 600 : 800 = 3 : 4 \(\frac{M}{L}\) = \(\frac{3}{4}\) \(\to\) M = \(\frac{3}{4}\)L \(\frac{3}{4}\)L + L = 28 \(\frac{7L}{4}\) = 28 L = \(\frac{4 \times 28}{7}\) = 16 |

