Year :
2019
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
71 - 80 of 80 Questions
| # | Question | Ans |
|---|---|---|
| 71. |
If y = 8x\(^3\) - 3x\(^2\) + 7x - 1, find \(\frac{\mathrm d^2 y}{\mathrm d x^2}\). A. 48x - 6 B. 11x\(^2\) + 6x - 7 C. 32x + 7 D. 24x\(^2\) - 6x + 7 Detailed Solutiony = 8x\(^3\) - 3x\(^2\) + 7x - 1\(\frac{\mathrm d^2 y}{\mathrm d x^2} = \frac{\mathrm d}{\mathrm d x} (\frac{\mathrm d y}{\mathrm d x})\) = \(\frac{\mathrm d}{\mathrm d x} (24x^2 - 6x + 7)\) \(\frac{\mathrm d^2 y}{\mathrm d x^2} = 48x - 6\) There is an explanation video available below. |
|
| 72. |
Differentiate \(\frac{2x}{\sin x}\) with respect to x. A. \(2 \cot x \sec x (1 + \tan x)\) B. \(2 \csc x - x \cot x\) C. \(2x \csc x + \tan x\) D. \(2\csc x(1 - x\cot x)\) |
|
| 73. |
Find the distance between the points C(2, 2) and D(5, 6). A. 13 units B. 7 units C. 12 units D. 5 units Detailed Solution= \(\sqrt{(5 - 2)^2 + (6 - 2)^2}\)= \(\sqrt{3^2 + 4^2}\) = \(\sqrt{9 + 16}\) = \(\sqrt{25}\) = 5 units There is an explanation video available below. |
|
| 74. |
Find the equation of a line perpendicular to the line 4y = 7x + 3 which passes through (-3, 1) A. 7y + 4x + 5 = 0 B. 7y - 4x - 5 = 0 C. 3y - 5x + 2 = 0 D. 3y + 5x - 2 = 0 Detailed SolutionEquation: 4y = 7x + 3\(\implies y = \frac{7}{4} x + \frac{3}{4}\) Slope = coefficient of x = \(\frac{7}{4}\) Slope of perpendicular line = \(\frac{-1}{\frac{7}{4}}\) = \(\frac{-4}{7}\) The perpendicular line passes (-3, 1) \(\therefore\) Using the equation of line \(y = mx + b\) m = slope and b = intercept. \(y = \frac{-4}{7} x + b\) To find the intercept, substitute y = 1 and x = -3 in the equation. \(1 = \frac{-4}{7} (-3) + b\) \(1 = \frac{12}{7} + b\) \(b = \frac{-5}{7}\) \(\therefore y = \frac{-4}{7} x - \frac{5}{7}\) \(7y + 4x + 5 = 0\) There is an explanation video available |
|
| 75. |
 Table:The table above is the distribution of data with mean equals to 3. Find the value of y. A. 5 B. 2 C. 3 D. 6 Detailed SolutionMean = \(\frac{\sum fx}{\sum f}\)\(3 = \frac{26 - y}{3y + 2}\) \(3(3y + 2) = 26 - y\) \(9y + 6 = 26 - y\) \(9y + y = 26 - 6\) \(10y = 20 \implies y = 2\) There is an explanation video available below. |
|
| 76. |
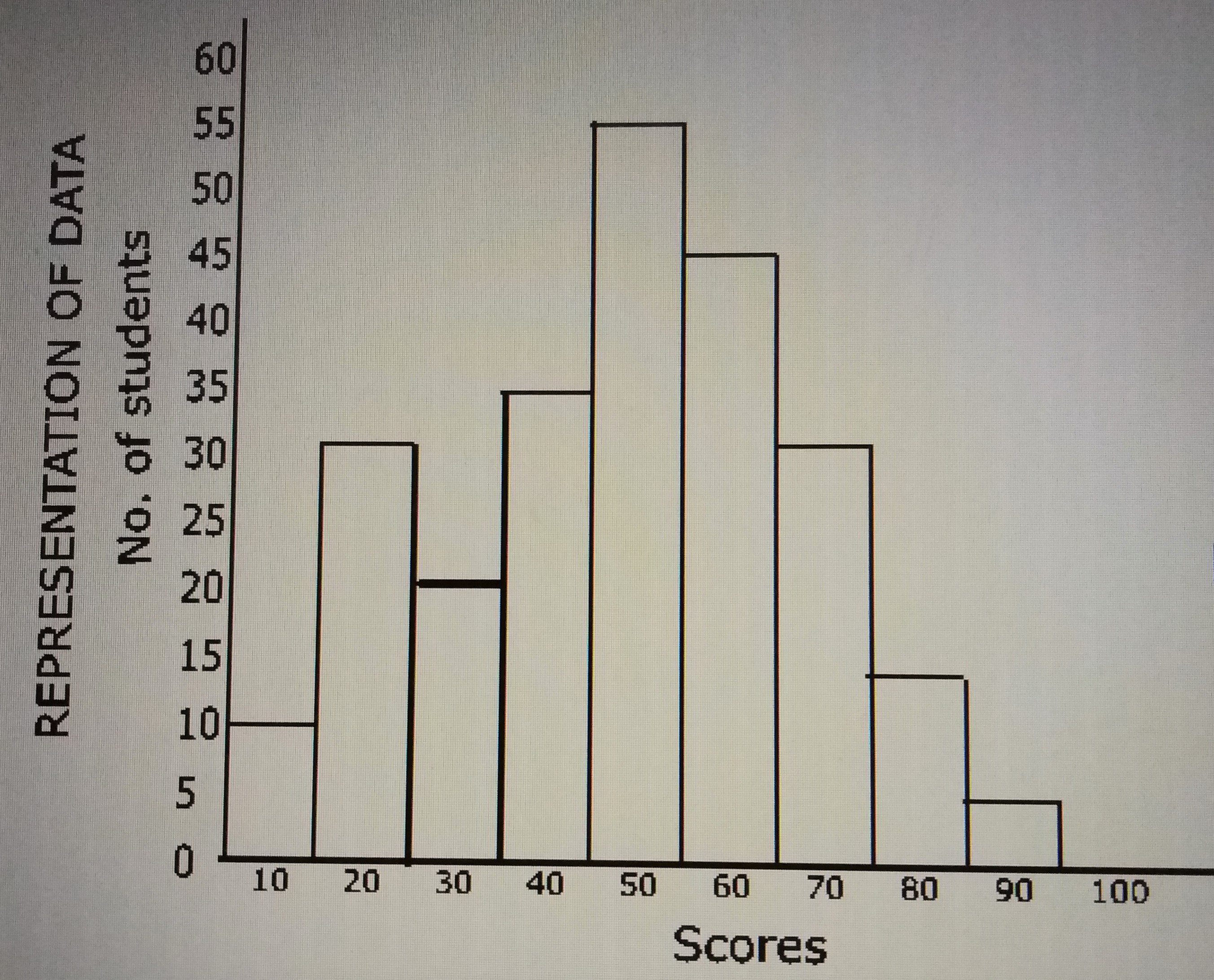 The histogram above represents the number of candidates who did Further Mathematics examination in a school. How many candidates scored more than 40? A. 100 B. 79 C. 150 D. 90 Detailed SolutionNumber of students that scored above 40 = 55 + 45 + 30 + 15 + 5= 150 students. There is an explanation video available below. |
|
| 77. |
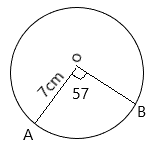 In the circle above, with centre O and radius 7 cm. Find the length of the arc AB, when < AOB = 57°. A. 5.32 cm B. 4.39 cm C. 7.33 cm D. 6.97 cm Detailed SolutionLength of arc = \(\frac{\theta}{360°} \times 2 \pi r\)= \(\frac{57}{360} \times 2 \times \frac{22}{7} \times 7\) = 6.97 cm There is an explanation video available below. |
|
| 78. |
 Calculate the volume of the regular three dimensional figure drawn above, where < ABC = 90° (a right- angled triangle). A. 394 cm\(^3\) B. 425 cm\(^3\) C. 268 cm\(^3\) D. 540 cm\(^3\) Detailed Solution|AC| = |DF| = 13 cmUsing Pythagoras theorem, |AC|\(^2\) = |AB|\(^2\) + |BC|\(^2\) 13\(^2\) = 12\(^2\) + |BC|\(^2\) |BC|\(^2\) = 169 - 144 = 25 |BC| = \(\sqrt{25}\) = 5 cm Volume of triangular prism = \(\frac{1}{2} \times base \times length \times height\) = \(\frac{1}{2} \times 5 \times 12 \times 18\) = 540 cm\(^3\) There is an explanation video available below. |
|
| 79. |
If \(\sin x = \frac{4}{5}\), find \(\frac{1 + \cot^2 x}{\csc^2 x - 1}\). A. \(\frac{13}{2}\) B. \(\frac{25}{9}\) C. \(\frac{3}{13}\) D. \(\frac{4}{11}\) Detailed Solution\(\sin x = \frac{opp}{Hyp} = \frac{4}{5}\)5\(^2\) = 4\(^2\) + adj\(^2\) adj\(^2\) = 25 - 16 = 9 adj = \(\sqrt{9}\) = 3 \(\tan x = \frac{4}{3}\) \(\cot x = \frac{1}{\frac{4}{3}} = \frac{3}{4}\) \(\cot^2 x = (\frac{3}{4})^2 = \frac{9}{16}\) \(\csc x = \frac{1}{\sin x}\) = \(\frac{1}{\frac{4}{5}} = \frac{5}{4}\) \(\csc^2 x = (\frac{5}{4})^2 = \frac{25}{16}\) \(\therefore \frac{1 + \cot^2 x}{\csc^2 x - 1} = \frac{1 + \frac{9}{16}}{\frac{25}{16} - 1}\) = \(\frac{25}{16} \div \frac{9}{16}\) = \(\frac{25}{9}\) There is an explanation video available below. |
|
| 80. |
Evaluate \(\frac{2\sin 30 + 5\tan 60}{\sin 60}\), leaving your answer in surd form. A. \(\frac{2\sqrt{3}}{3} + 10\) B. \(\frac{3\sqrt{2} - 1}{5}\) C. \(\frac{3\sqrt{2} + 1}{5}\) D. \(\frac{2\sqrt{3}}{3} - 10\) Detailed Solution\(\frac{2\sin 30 + 5\tan 60}{\sin 60}\)\(\sin 30 = \frac{1}{2}; \tan 60 = \sqrt{3}; \sin 60 = \frac{\sqrt{3}}{2}\) \(\therefore \frac{2\sin 30 + 5\tan 60}{\sin 60} = \frac{2(\frac{1}{2}) + 5(\sqrt{3})}{\frac{\sqrt{3}}{2}}\)\) = \(\frac{1 + 5\sqrt{3}}{\frac{\sqrt{3}}{2}}\) = \(\frac{2(1 + 5\sqrt{3})}{\sqrt{3}}\) = \(\frac{2 + 10\sqrt{3}}{\sqrt{3}}\) Rationalizing, we get = \(\frac{2\sqrt{3} + 30}{3}\) = \(\frac{2}{3} \sqrt{3} + 10\) There is an explanation video available below. |
| 71. |
If y = 8x\(^3\) - 3x\(^2\) + 7x - 1, find \(\frac{\mathrm d^2 y}{\mathrm d x^2}\). A. 48x - 6 B. 11x\(^2\) + 6x - 7 C. 32x + 7 D. 24x\(^2\) - 6x + 7 Detailed Solutiony = 8x\(^3\) - 3x\(^2\) + 7x - 1\(\frac{\mathrm d^2 y}{\mathrm d x^2} = \frac{\mathrm d}{\mathrm d x} (\frac{\mathrm d y}{\mathrm d x})\) = \(\frac{\mathrm d}{\mathrm d x} (24x^2 - 6x + 7)\) \(\frac{\mathrm d^2 y}{\mathrm d x^2} = 48x - 6\) There is an explanation video available below. |
|
| 72. |
Differentiate \(\frac{2x}{\sin x}\) with respect to x. A. \(2 \cot x \sec x (1 + \tan x)\) B. \(2 \csc x - x \cot x\) C. \(2x \csc x + \tan x\) D. \(2\csc x(1 - x\cot x)\) |
|
| 73. |
Find the distance between the points C(2, 2) and D(5, 6). A. 13 units B. 7 units C. 12 units D. 5 units Detailed Solution= \(\sqrt{(5 - 2)^2 + (6 - 2)^2}\)= \(\sqrt{3^2 + 4^2}\) = \(\sqrt{9 + 16}\) = \(\sqrt{25}\) = 5 units There is an explanation video available below. |
|
| 74. |
Find the equation of a line perpendicular to the line 4y = 7x + 3 which passes through (-3, 1) A. 7y + 4x + 5 = 0 B. 7y - 4x - 5 = 0 C. 3y - 5x + 2 = 0 D. 3y + 5x - 2 = 0 Detailed SolutionEquation: 4y = 7x + 3\(\implies y = \frac{7}{4} x + \frac{3}{4}\) Slope = coefficient of x = \(\frac{7}{4}\) Slope of perpendicular line = \(\frac{-1}{\frac{7}{4}}\) = \(\frac{-4}{7}\) The perpendicular line passes (-3, 1) \(\therefore\) Using the equation of line \(y = mx + b\) m = slope and b = intercept. \(y = \frac{-4}{7} x + b\) To find the intercept, substitute y = 1 and x = -3 in the equation. \(1 = \frac{-4}{7} (-3) + b\) \(1 = \frac{12}{7} + b\) \(b = \frac{-5}{7}\) \(\therefore y = \frac{-4}{7} x - \frac{5}{7}\) \(7y + 4x + 5 = 0\) There is an explanation video available |
|
| 75. |
 Table:The table above is the distribution of data with mean equals to 3. Find the value of y. A. 5 B. 2 C. 3 D. 6 Detailed SolutionMean = \(\frac{\sum fx}{\sum f}\)\(3 = \frac{26 - y}{3y + 2}\) \(3(3y + 2) = 26 - y\) \(9y + 6 = 26 - y\) \(9y + y = 26 - 6\) \(10y = 20 \implies y = 2\) There is an explanation video available below. |
| 76. |
 The histogram above represents the number of candidates who did Further Mathematics examination in a school. How many candidates scored more than 40? A. 100 B. 79 C. 150 D. 90 Detailed SolutionNumber of students that scored above 40 = 55 + 45 + 30 + 15 + 5= 150 students. There is an explanation video available below. |
|
| 77. |
 In the circle above, with centre O and radius 7 cm. Find the length of the arc AB, when < AOB = 57°. A. 5.32 cm B. 4.39 cm C. 7.33 cm D. 6.97 cm Detailed SolutionLength of arc = \(\frac{\theta}{360°} \times 2 \pi r\)= \(\frac{57}{360} \times 2 \times \frac{22}{7} \times 7\) = 6.97 cm There is an explanation video available below. |
|
| 78. |
 Calculate the volume of the regular three dimensional figure drawn above, where < ABC = 90° (a right- angled triangle). A. 394 cm\(^3\) B. 425 cm\(^3\) C. 268 cm\(^3\) D. 540 cm\(^3\) Detailed Solution|AC| = |DF| = 13 cmUsing Pythagoras theorem, |AC|\(^2\) = |AB|\(^2\) + |BC|\(^2\) 13\(^2\) = 12\(^2\) + |BC|\(^2\) |BC|\(^2\) = 169 - 144 = 25 |BC| = \(\sqrt{25}\) = 5 cm Volume of triangular prism = \(\frac{1}{2} \times base \times length \times height\) = \(\frac{1}{2} \times 5 \times 12 \times 18\) = 540 cm\(^3\) There is an explanation video available below. |
|
| 79. |
If \(\sin x = \frac{4}{5}\), find \(\frac{1 + \cot^2 x}{\csc^2 x - 1}\). A. \(\frac{13}{2}\) B. \(\frac{25}{9}\) C. \(\frac{3}{13}\) D. \(\frac{4}{11}\) Detailed Solution\(\sin x = \frac{opp}{Hyp} = \frac{4}{5}\)5\(^2\) = 4\(^2\) + adj\(^2\) adj\(^2\) = 25 - 16 = 9 adj = \(\sqrt{9}\) = 3 \(\tan x = \frac{4}{3}\) \(\cot x = \frac{1}{\frac{4}{3}} = \frac{3}{4}\) \(\cot^2 x = (\frac{3}{4})^2 = \frac{9}{16}\) \(\csc x = \frac{1}{\sin x}\) = \(\frac{1}{\frac{4}{5}} = \frac{5}{4}\) \(\csc^2 x = (\frac{5}{4})^2 = \frac{25}{16}\) \(\therefore \frac{1 + \cot^2 x}{\csc^2 x - 1} = \frac{1 + \frac{9}{16}}{\frac{25}{16} - 1}\) = \(\frac{25}{16} \div \frac{9}{16}\) = \(\frac{25}{9}\) There is an explanation video available below. |
|
| 80. |
Evaluate \(\frac{2\sin 30 + 5\tan 60}{\sin 60}\), leaving your answer in surd form. A. \(\frac{2\sqrt{3}}{3} + 10\) B. \(\frac{3\sqrt{2} - 1}{5}\) C. \(\frac{3\sqrt{2} + 1}{5}\) D. \(\frac{2\sqrt{3}}{3} - 10\) Detailed Solution\(\frac{2\sin 30 + 5\tan 60}{\sin 60}\)\(\sin 30 = \frac{1}{2}; \tan 60 = \sqrt{3}; \sin 60 = \frac{\sqrt{3}}{2}\) \(\therefore \frac{2\sin 30 + 5\tan 60}{\sin 60} = \frac{2(\frac{1}{2}) + 5(\sqrt{3})}{\frac{\sqrt{3}}{2}}\)\) = \(\frac{1 + 5\sqrt{3}}{\frac{\sqrt{3}}{2}}\) = \(\frac{2(1 + 5\sqrt{3})}{\sqrt{3}}\) = \(\frac{2 + 10\sqrt{3}}{\sqrt{3}}\) Rationalizing, we get = \(\frac{2\sqrt{3} + 30}{3}\) = \(\frac{2}{3} \sqrt{3} + 10\) There is an explanation video available below. |