Year : 
2019
Title : 
Mathematics (Core)
Exam : 
JAMB Exam

Paper 1 | Objectives

11 - 20 of 80 Questions

# Question Ans
11.

If a fair coin is tossed 3 times, what is the probability of getting at least two heads?

A. \(\frac{2}{3}\)

B. \(\frac{4}{5}\)

C. \(\frac{2}{5}\)

D. \(\frac{1}{2}\)

Detailed Solution

The outcomes are {HHH, HHT, HTT, HTH, THH, THT, TTH, TTT}
P(at least two heads) = \(\frac{4}{8}\)
= \(\frac{1}{2}\)
There is an explanation video available below.
12.

In how many ways can the word MATHEMATICIAN be arranged?

A. 6794800 ways

B. 2664910 ways

C. 6227020800 ways

D. 129729600 ways

Detailed Solution

MATHEMATICIAN = 13 letters with 2M, 3A, 2T, 2I.
Hence, the word MATHEMATICIAN can be arranged in \(\frac{13!}{2! 3! 2! 2!}\)
= 129729600 ways
There is an explanation video available below.
13.

Given matrix M = \(\begin{vmatrix} -2 & 0 & 4 \\ 0 & -1 & 6 \\ 5 & 6 & 3 \end{vmatrix}\), find \(M^{T} + 2M\)

A. \(\begin{vmatrix} -4 & 2 & 1\\ 6 & 0 & 5 \\ 0 & 6 & 2 \end{vmatrix}\)

B. \(\begin{vmatrix} -6 & 0 & 13\\ 0 & -3 & 18 \\ 14 & 18 & 9 \end{vmatrix}\)

C. \(\begin{vmatrix} 5 & 2 & 6 \\ 0 & 1 & 1\\ 3 & 4 & -7 \end{vmatrix}\)

D. \(\begin{vmatrix} -4 & 0 & 8 \\ 0 & -2 & -16 \\ 10 & 12 & 6 \end{vmatrix}\)

Detailed Solution

M = \(\begin{vmatrix} -2 & 0 & 4 \\ 0 & -1 & 6 \\ 5 & 6 & 3 \end{vmatrix}\)
M\(^{T}\) = \(\begin{vmatrix} -2 & 0 & 5 \\ 0 & -1 & 6\\ 4 & 6 & 3 \end{vmatrix}\)
2M = \(\begin{vmatrix} -4 & 0 & 8\\ 0 & -2 & 12\\ 10 & 12 & 6\end{vmatrix}\)
M\(^T\) + 2M = \(\begin{vmatrix} -6 & 0 & 13 \\ 0 & -3 & 18 \\ 14 & 18 & 9 \end{vmatrix}\)
There is an explanation video available below.
14.

Table:
Find the mean of the data.

A. 3.26

B. 4.91

C. 6.57

D. 3.0

Detailed Solution

Mean = \(\frac{\sum fx}{\sum f}\)
= \(\frac{150}{46}\)
= 3.26
There is an explanation video available below.
15.

Table:
Find the variance

A. 3.42

B. 4.69

C. 4.85

D. 3.72

Detailed Solution

Variance = \(\frac{\sum f(x - \bar{x})}{\sum f}\)
= \(\frac{170.888}{46}\)
= 3.72

There is an explanation video available below.
16.

The locus of a point which moves so that it is equidistant from two intersecting straight lines is the

A. bisector of the two lines

B. line parallel to the two lines

C. angle bisector of the two lines

D. perpendicular bisector of the two lines

Detailed Solution

The locus of a points equidistant from two intersecting straight lines is a pair of bisectors that bisect the angles formed by the two intersecting lines.
There is an explanation video available below.
17.

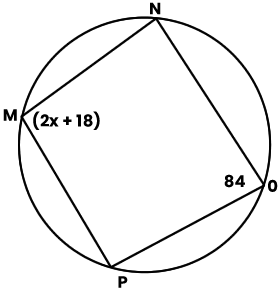From the cyclic quadrilateral MNOP above, find the value of x.

A. 16°

B. 25°

C. 42°

D. 39°

Detailed Solution

The sum of two opposite angles of a cyclic quadrilateral = 180°
\(\therefore\) (2x + 18)° + 84° = 180°
2x + 102° = 180° \(\implies\) 2x = 78°
x = 39°
There is an explanation video available below.
18.

If \(4\sin^2 x - 3 = 0\), find the value of x, when 0° \(\leq\) x \(\leq\) 90°

A. 90°

B. 45°

C. 60°

D. 30°

Detailed Solution

\(4\sin^2 x - 3 = 0\)
\(4 \sin^2 x = 3 \implies \sin^2 x = \frac{3}{4}\)
\(\sin x = \frac{\sqrt{3}}{2}\)
\(\therefore x = \sin^{-1} (\frac{\sqrt{3}}{2})\)
x = 60°
There is an explanation video available below.
19.

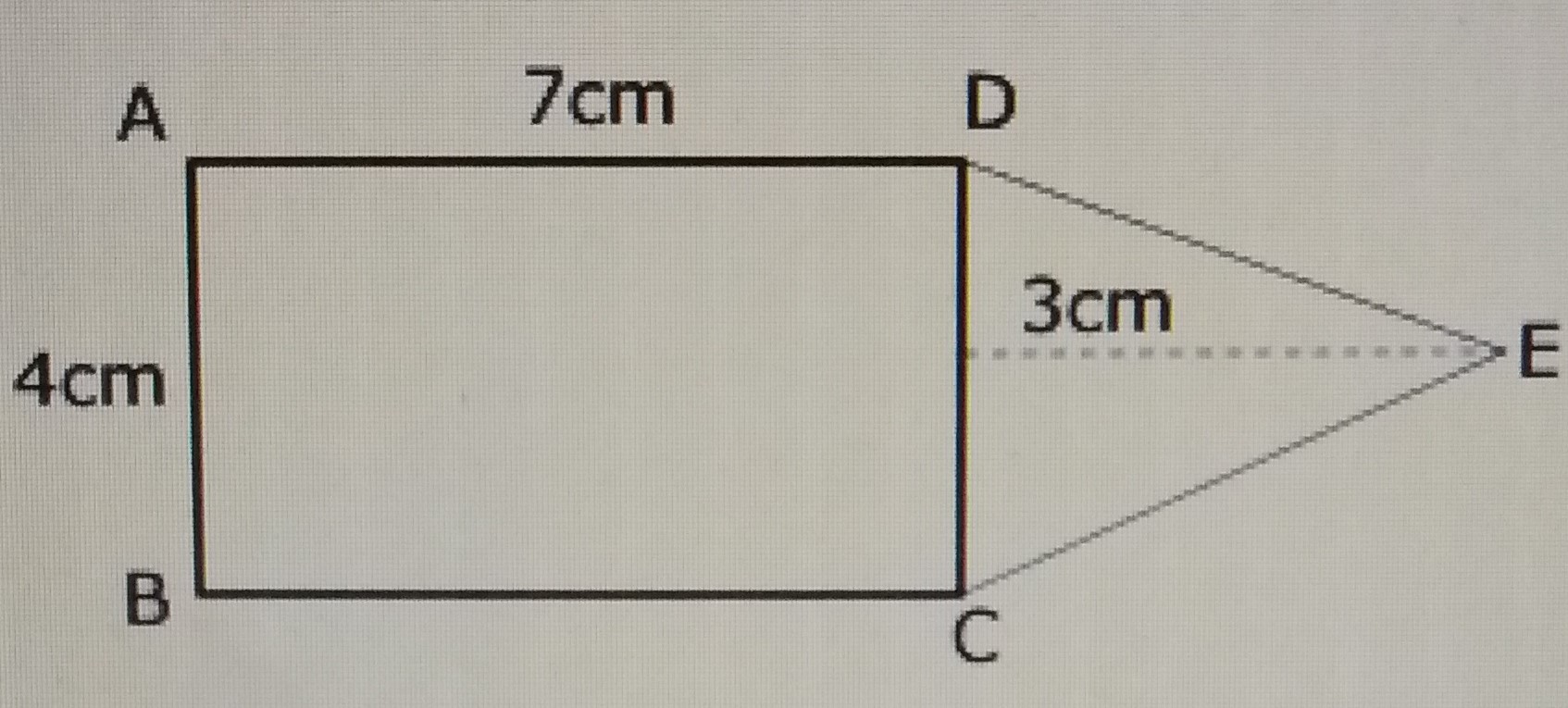In the figure above, |CD| is the base of the triangle CDE. Find the area of the figure to the nearest whole number.

A. 56 cm\(^2\)

B. 24 cm\(^2\)

C. 42 cm\(^2\)

D. 34 cm\(^2\)

Detailed Solution

Area of rectangle ABCD = length x breadth
= 7 x 4
= 28 cm\(^2\)
Area of triangle CDE = \(\frac{1}{2}\) base x height
= \(\frac{1}{2} \times 3 \times 4\)
= 6 cm\(^2\)
Area of the figure = 28 cm\(^2\) + 6 cm\(^2\)
= 34 cm\(^2\)
There is an explanation video available below.
20.

Table:
The marks scored by 30 students in a Mathematics test are recorded in the table below:What is the total number of marks scored by the children?

A. 82

B. 15

C. 63

D. 75

Detailed Solution


There is an explanation video available below.
11.

If a fair coin is tossed 3 times, what is the probability of getting at least two heads?

A. \(\frac{2}{3}\)

B. \(\frac{4}{5}\)

C. \(\frac{2}{5}\)

D. \(\frac{1}{2}\)

Detailed Solution

The outcomes are {HHH, HHT, HTT, HTH, THH, THT, TTH, TTT}
P(at least two heads) = \(\frac{4}{8}\)
= \(\frac{1}{2}\)
There is an explanation video available below.
12.

In how many ways can the word MATHEMATICIAN be arranged?

A. 6794800 ways

B. 2664910 ways

C. 6227020800 ways

D. 129729600 ways

Detailed Solution

MATHEMATICIAN = 13 letters with 2M, 3A, 2T, 2I.
Hence, the word MATHEMATICIAN can be arranged in \(\frac{13!}{2! 3! 2! 2!}\)
= 129729600 ways
There is an explanation video available below.
13.

Given matrix M = \(\begin{vmatrix} -2 & 0 & 4 \\ 0 & -1 & 6 \\ 5 & 6 & 3 \end{vmatrix}\), find \(M^{T} + 2M\)

A. \(\begin{vmatrix} -4 & 2 & 1\\ 6 & 0 & 5 \\ 0 & 6 & 2 \end{vmatrix}\)

B. \(\begin{vmatrix} -6 & 0 & 13\\ 0 & -3 & 18 \\ 14 & 18 & 9 \end{vmatrix}\)

C. \(\begin{vmatrix} 5 & 2 & 6 \\ 0 & 1 & 1\\ 3 & 4 & -7 \end{vmatrix}\)

D. \(\begin{vmatrix} -4 & 0 & 8 \\ 0 & -2 & -16 \\ 10 & 12 & 6 \end{vmatrix}\)

Detailed Solution

M = \(\begin{vmatrix} -2 & 0 & 4 \\ 0 & -1 & 6 \\ 5 & 6 & 3 \end{vmatrix}\)
M\(^{T}\) = \(\begin{vmatrix} -2 & 0 & 5 \\ 0 & -1 & 6\\ 4 & 6 & 3 \end{vmatrix}\)
2M = \(\begin{vmatrix} -4 & 0 & 8\\ 0 & -2 & 12\\ 10 & 12 & 6\end{vmatrix}\)
M\(^T\) + 2M = \(\begin{vmatrix} -6 & 0 & 13 \\ 0 & -3 & 18 \\ 14 & 18 & 9 \end{vmatrix}\)
There is an explanation video available below.
14.

Table:
Find the mean of the data.

A. 3.26

B. 4.91

C. 6.57

D. 3.0

Detailed Solution

Mean = \(\frac{\sum fx}{\sum f}\)
= \(\frac{150}{46}\)
= 3.26
There is an explanation video available below.
15.

Table:
Find the variance

A. 3.42

B. 4.69

C. 4.85

D. 3.72

Detailed Solution

Variance = \(\frac{\sum f(x - \bar{x})}{\sum f}\)
= \(\frac{170.888}{46}\)
= 3.72

There is an explanation video available below.
16.

The locus of a point which moves so that it is equidistant from two intersecting straight lines is the

A. bisector of the two lines

B. line parallel to the two lines

C. angle bisector of the two lines

D. perpendicular bisector of the two lines

Detailed Solution

The locus of a points equidistant from two intersecting straight lines is a pair of bisectors that bisect the angles formed by the two intersecting lines.
There is an explanation video available below.
17.

From the cyclic quadrilateral MNOP above, find the value of x.

A. 16°

B. 25°

C. 42°

D. 39°

Detailed Solution

The sum of two opposite angles of a cyclic quadrilateral = 180°
\(\therefore\) (2x + 18)° + 84° = 180°
2x + 102° = 180° \(\implies\) 2x = 78°
x = 39°
There is an explanation video available below.
18.

If \(4\sin^2 x - 3 = 0\), find the value of x, when 0° \(\leq\) x \(\leq\) 90°

A. 90°

B. 45°

C. 60°

D. 30°

Detailed Solution

\(4\sin^2 x - 3 = 0\)
\(4 \sin^2 x = 3 \implies \sin^2 x = \frac{3}{4}\)
\(\sin x = \frac{\sqrt{3}}{2}\)
\(\therefore x = \sin^{-1} (\frac{\sqrt{3}}{2})\)
x = 60°
There is an explanation video available below.
19.

In the figure above, |CD| is the base of the triangle CDE. Find the area of the figure to the nearest whole number.

A. 56 cm\(^2\)

B. 24 cm\(^2\)

C. 42 cm\(^2\)

D. 34 cm\(^2\)

Detailed Solution

Area of rectangle ABCD = length x breadth
= 7 x 4
= 28 cm\(^2\)
Area of triangle CDE = \(\frac{1}{2}\) base x height
= \(\frac{1}{2} \times 3 \times 4\)
= 6 cm\(^2\)
Area of the figure = 28 cm\(^2\) + 6 cm\(^2\)
= 34 cm\(^2\)
There is an explanation video available below.
20.

Table:
The marks scored by 30 students in a Mathematics test are recorded in the table below:What is the total number of marks scored by the children?

A. 82

B. 15

C. 63

D. 75

Detailed Solution


There is an explanation video available below.