Year :
2019
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 50 of 80 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
Simplify \(\frac{0.0839 \times 6.381}{5.44}\) to 2 significant figures. A. 0.2809 B. 2.51 C. 3.5 D. 0.098 |
|
| 42. |
Find the value of x and y in the simultaneous equation: 3x + y = 21; xy = 30 A. x = 3 or 7, y = 12 or 8 B. x = 6 or 1, y = 11 or 5 C. x = 2 or 5, y = 15 or 6 D. x = 1 or 5, y = 10 or 7 Detailed Solution3x + y = 21 ... (i);xy = 30 ... (ii) From (ii), \(y = \frac{30}{x}\). Putting the value of y in (i), we have 3x + \(\frac{30}{x}\) = 21 \(\implies\) 3x\(^2\) + 30 = 21x 3x\(^2\) - 21x + 30 = 0 3x\(^2\) - 15x - 6x + 30 = 0 3x(x - 5) - 6(x - 5) = 0 (3x - 6)(x - 5) = 0 3x - 6 = 0 \(\implies\) x = 2. x - 5 = 0 \(\implies\) x = 5. If x = 2, y = \(\frac{30}{2}\) = 15; If x = 5, y = \(\frac{30}{5}\) = 6. There is an explanation video available below. |
|
| 43. |
Points X and Y are 20km North and 9km East of point O, respectively. What is the bearing of Y from X? Correct to the nearest degree. A. 24° B. 56° C. 127° D. 156° Detailed Solution \(\tan \theta = \frac{9}{20} = 0.45\) \(\theta = \tan^{-1} (0.45) \) = 24.23° \(\therefore\) The bearing of Y from X = 180° - 24.23° = 155.77° = 156° (to the nearest degree) There is an explanation video available below. |
|
| 44. |
If \(P = (\frac{Q(R - T)}{15})^{\frac{1}{3}}\), make T the subject of the formula. A. \(T = \frac{15R - Q}{P^3}\) B. \(T = R - \frac{15P^3}{Q}\) C. \(T = \frac{R - 15P^3}{Q}\) D. \(T = \frac{R + P^3}{15Q}\) Detailed Solution\(P = (\frac{Q(R - T)}{15})^{\frac{1}{3}}\)\(P^3 = \frac{Q(R - T)}{15}\) \(Q(R - T) = 15P^3\) \(R - T = \frac{15P^3}{Q}\) \(T = R - \frac{15P^3}{Q}\) There is an explanation video available below. |
|
| 45. |
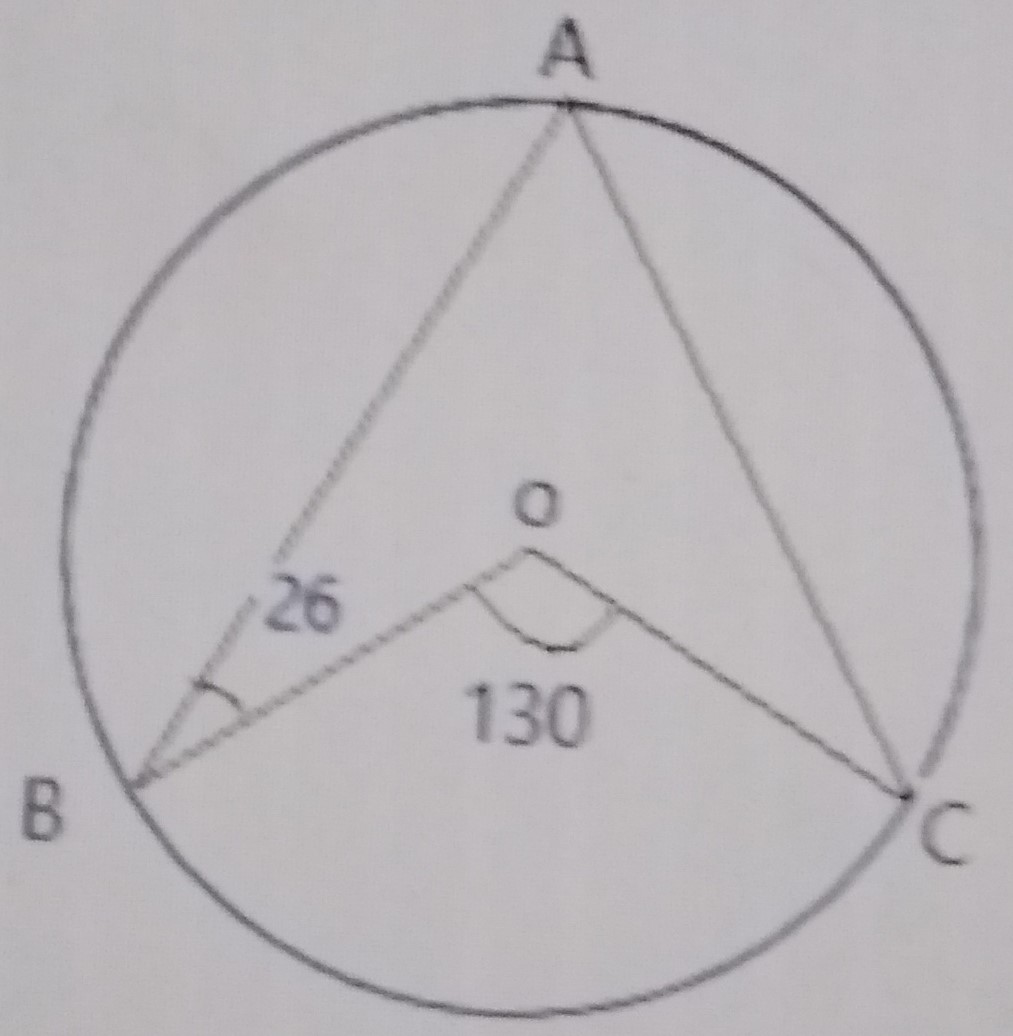 In the diagram above, O is the centre of the circle ABC, < ABO = 26° and < BOC = 130°. Calculate < AOC. A. 26° B. 13° C. 80° D. 102° Detailed Solution < BAC = \(\frac{130}{2}\) (angle subtended at the centre) < BAC = 65° Also, x = 26° (theorem) y = 65° - 26° = 39° < AOC = 180° - (39° + 39°) = 102° There is an explanation video available below. |
|
| 46. |
Each of the interior angles of a regular polygon is 140°. Calculate the sum of all the interior angles of the polygon. A. 1080° B. 1260° C. 2160° D. 1800° Detailed SolutionSince each interior angle = 140°;Each exterior angle = 180° - 140° = 40° Number of sides of the polygon = \(\frac{360°}{40°}\) = 9 Sum of angles in the polygon = 140° x 9 = 1260° There is an explanation video available below. |
|
| 47. |
A man bought a car newly for ₦1,250,000. He had a crash with the car and later sold it at the rate of ₦1,085,000. What is the percentage gain or loss of the man? A. 43.7% loss B. 13.2% gain C. 13.2% loss D. 43.7% gain Detailed SolutionCost price of the car = N 1,250.00Selling price = N 1,085.00 Loss = N (1250 - 1085) = N 165.00 % loss = \(\frac{165}{1250} \times 100%\) = 13.2% loss There is an explanation video available below. |
|
| 48. |
If the volume of a frustrum is given as \(V = \frac{\pi h}{3} (R^2 + Rr + r^2)\), find \(\frac{\mathrm d V}{\mathrm d R}\). A. \(\frac{\pi h}{3} (2R + r)\) B. \(2R + r + \frac{\pi h}{3}\) C. \(\frac{\pi h}{3} (2R^2 + r + 2r)\) D. \(\frac{2R^2}{3} \pi h\) Detailed Solution\(V = \frac{\pi h}{3} (R^2 + Rr + r^2)\)\(V = \frac{\pi R^2 h}{3} + \frac{\pi Rr h}{3} + \frac{\pi r^2 h}{3}\) \(\frac{\mathrm d V}{\mathrm d R} = \frac{2 \pi R h}{3} + \frac{\pi r h}{3}\) = \(\frac{\pi}{3} (2R + r)\) There is an explanation video available below. |
|
| 49. |
Express \((0.0439 \div 3.62)\) as a fraction. A. \(\frac{21}{100}\) B. \(\frac{21}{1000}\) C. \(\frac{12}{1000}\) D. \(\frac{12}{100}\) Detailed Solution\((0.0439 \div 3.62)\)= 0.01213 \(\approxeq\) 0.012 = \(\frac{12}{1000}\) There is an explanation video available below. |
|
| 50. |
If \(25^{1 - x} \times 5^{x + 2} \div (\frac{1}{125})^{x} = 625^{-1}\), find the value of x. A. x = -4 B. x = 2 C. x = -2 D. x = 4 Detailed Solution\(25^{1 - x} \times 5^{x + 2} \div (\frac{1}{125})^{x} = 625^{-1}\)\((5^2)^{(1 - x)} \times 5^{(x + 2)} \div (5^{-3})^x = (5^4)^{-1}\) \(5^{2 - 2x} \times 5^{x + 2} \div 5^{-3x} = 5^{-4}\) \(5^{(2 - 2x) + (x + 2) - (-3x)} = 5^{-4}\) Equating bases, we have \(2 - 2x + x + 2 + 3x = -4\) \(4 + 2x = -4 \implies 2x = -4 - 4\) \(2x = -8\) \(x = -4\) There is an explanation video available below. |
| 41. |
Simplify \(\frac{0.0839 \times 6.381}{5.44}\) to 2 significant figures. A. 0.2809 B. 2.51 C. 3.5 D. 0.098 |
|
| 42. |
Find the value of x and y in the simultaneous equation: 3x + y = 21; xy = 30 A. x = 3 or 7, y = 12 or 8 B. x = 6 or 1, y = 11 or 5 C. x = 2 or 5, y = 15 or 6 D. x = 1 or 5, y = 10 or 7 Detailed Solution3x + y = 21 ... (i);xy = 30 ... (ii) From (ii), \(y = \frac{30}{x}\). Putting the value of y in (i), we have 3x + \(\frac{30}{x}\) = 21 \(\implies\) 3x\(^2\) + 30 = 21x 3x\(^2\) - 21x + 30 = 0 3x\(^2\) - 15x - 6x + 30 = 0 3x(x - 5) - 6(x - 5) = 0 (3x - 6)(x - 5) = 0 3x - 6 = 0 \(\implies\) x = 2. x - 5 = 0 \(\implies\) x = 5. If x = 2, y = \(\frac{30}{2}\) = 15; If x = 5, y = \(\frac{30}{5}\) = 6. There is an explanation video available below. |
|
| 43. |
Points X and Y are 20km North and 9km East of point O, respectively. What is the bearing of Y from X? Correct to the nearest degree. A. 24° B. 56° C. 127° D. 156° Detailed Solution \(\tan \theta = \frac{9}{20} = 0.45\) \(\theta = \tan^{-1} (0.45) \) = 24.23° \(\therefore\) The bearing of Y from X = 180° - 24.23° = 155.77° = 156° (to the nearest degree) There is an explanation video available below. |
|
| 44. |
If \(P = (\frac{Q(R - T)}{15})^{\frac{1}{3}}\), make T the subject of the formula. A. \(T = \frac{15R - Q}{P^3}\) B. \(T = R - \frac{15P^3}{Q}\) C. \(T = \frac{R - 15P^3}{Q}\) D. \(T = \frac{R + P^3}{15Q}\) Detailed Solution\(P = (\frac{Q(R - T)}{15})^{\frac{1}{3}}\)\(P^3 = \frac{Q(R - T)}{15}\) \(Q(R - T) = 15P^3\) \(R - T = \frac{15P^3}{Q}\) \(T = R - \frac{15P^3}{Q}\) There is an explanation video available below. |
|
| 45. |
 In the diagram above, O is the centre of the circle ABC, < ABO = 26° and < BOC = 130°. Calculate < AOC. A. 26° B. 13° C. 80° D. 102° Detailed Solution < BAC = \(\frac{130}{2}\) (angle subtended at the centre) < BAC = 65° Also, x = 26° (theorem) y = 65° - 26° = 39° < AOC = 180° - (39° + 39°) = 102° There is an explanation video available below. |
| 46. |
Each of the interior angles of a regular polygon is 140°. Calculate the sum of all the interior angles of the polygon. A. 1080° B. 1260° C. 2160° D. 1800° Detailed SolutionSince each interior angle = 140°;Each exterior angle = 180° - 140° = 40° Number of sides of the polygon = \(\frac{360°}{40°}\) = 9 Sum of angles in the polygon = 140° x 9 = 1260° There is an explanation video available below. |
|
| 47. |
A man bought a car newly for ₦1,250,000. He had a crash with the car and later sold it at the rate of ₦1,085,000. What is the percentage gain or loss of the man? A. 43.7% loss B. 13.2% gain C. 13.2% loss D. 43.7% gain Detailed SolutionCost price of the car = N 1,250.00Selling price = N 1,085.00 Loss = N (1250 - 1085) = N 165.00 % loss = \(\frac{165}{1250} \times 100%\) = 13.2% loss There is an explanation video available below. |
|
| 48. |
If the volume of a frustrum is given as \(V = \frac{\pi h}{3} (R^2 + Rr + r^2)\), find \(\frac{\mathrm d V}{\mathrm d R}\). A. \(\frac{\pi h}{3} (2R + r)\) B. \(2R + r + \frac{\pi h}{3}\) C. \(\frac{\pi h}{3} (2R^2 + r + 2r)\) D. \(\frac{2R^2}{3} \pi h\) Detailed Solution\(V = \frac{\pi h}{3} (R^2 + Rr + r^2)\)\(V = \frac{\pi R^2 h}{3} + \frac{\pi Rr h}{3} + \frac{\pi r^2 h}{3}\) \(\frac{\mathrm d V}{\mathrm d R} = \frac{2 \pi R h}{3} + \frac{\pi r h}{3}\) = \(\frac{\pi}{3} (2R + r)\) There is an explanation video available below. |
|
| 49. |
Express \((0.0439 \div 3.62)\) as a fraction. A. \(\frac{21}{100}\) B. \(\frac{21}{1000}\) C. \(\frac{12}{1000}\) D. \(\frac{12}{100}\) Detailed Solution\((0.0439 \div 3.62)\)= 0.01213 \(\approxeq\) 0.012 = \(\frac{12}{1000}\) There is an explanation video available below. |
|
| 50. |
If \(25^{1 - x} \times 5^{x + 2} \div (\frac{1}{125})^{x} = 625^{-1}\), find the value of x. A. x = -4 B. x = 2 C. x = -2 D. x = 4 Detailed Solution\(25^{1 - x} \times 5^{x + 2} \div (\frac{1}{125})^{x} = 625^{-1}\)\((5^2)^{(1 - x)} \times 5^{(x + 2)} \div (5^{-3})^x = (5^4)^{-1}\) \(5^{2 - 2x} \times 5^{x + 2} \div 5^{-3x} = 5^{-4}\) \(5^{(2 - 2x) + (x + 2) - (-3x)} = 5^{-4}\) Equating bases, we have \(2 - 2x + x + 2 + 3x = -4\) \(4 + 2x = -4 \implies 2x = -4 - 4\) \(2x = -8\) \(x = -4\) There is an explanation video available below. |