Mathematics (Core)
Paper 1 | Objectives | 40 Questions
JAMB Exam
Year: 2021
Level: SHS
Time:
Type: Question Paper
Answers provided
FREE
No description provided
Feedbacks
This paper is yet to be rated
Paper 1 | Objectives | 40 Questions
JAMB Exam
Year: 2021
Level: SHS
Time:
Type: Question Paper
Answers provided
No description provided
This paper is yet to be rated
| # | Question | Ans |
|---|---|---|
| 1. |
Solve the following equation: \(\frac{2}{(2r - 1)}\) - \(\frac{5}{3}\) = \(\frac{1}{(r + 2)}\) A. ( -1,\(\frac{5}{2}\) ) B. ( 1, - \(\frac{5}{2}\) ) C. ( \(\frac{5}{2}\), 1 ) D. (2,1) Detailed Solution\(\frac{2}{(2r - 1)}\) - \(\frac{5}{3}\) = \(\frac{1}{(r + 2)}\)\(\frac{2}{(2r - 1)}\) - \(\frac{1}{(r + 2)}\) = \(\frac{5}{3}\) The L.C.M.: (2r - 1) (r + 2) \(\frac{2(r + 2) - 1(2r - 1)}{(2r - 1) (r + 2)}\) = \(\frac{5}{3}\) \(\frac{2r + 4 - 2r + 1}{ (2r - 1) (r + 2)}\) = \(\frac{5}{3}\) cross multiply the solution 3 = (2r - 1) (r + 2) or 2r\(^2\) + 3r - 2 (when expanded) collect like terms 2r\(^2\) + 3r - 2 - 3 = 0 2r\(^2\) + 3r - 5 = 0 Factorize to get x = 1 or - \(\frac{5}{2}\) There is an explanation video available below. |
|
| 2. |
In how many ways can 2 students be selected from a group of 5 students in a debating competition? A. 25 ways B. 10 ways C. 15 ways D. 20 ways Detailed Solution\(In\hspace{1mm} ^{5}C_{2}\hspace{1mm}ways\hspace{1mm}=\frac{5!}{(5-2)!2!}\\=\frac{5!}{3!2!}\\=\frac{5\times4\times3!}{3!\times2\times1}\\=10\hspace{1mm}ways\)There is an explanation video available below. |
|
| 3. |
What is the rate of change of the volume V of a hemisphere with respect to its radius r when r = 2? A. 8π B. 16π C. 2π D. 4π Detailed Solution\(V = \frac{2}{3} \pi r^{3}\)\(\frac{\mathrm d V}{\mathrm d r} = 2\pi r^{2}\) \(\frac{\mathrm d V}{\mathrm d r} (r = 2) = 2\pi (2)^{2}\) = \(8\pi\) There is an explanation video available below. |
|
| 4. |
Determine the maximum value of y=3x\(^2\) + 5x - 3 A. 6 B. 0 C. 2 D. No correct option |
|
| 5. |
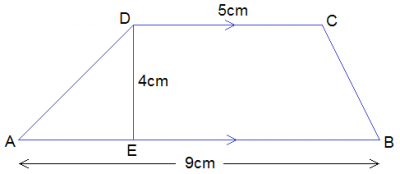 A trapezium has two parallel sides of lengths 5cm and 9cm. If the area is 91cm\(^2\), find the distance between the parallel sides A. 13 cm B. 4 cm C. 6 cm D. 7 cm Detailed SolutionArea of Trapezium = 1/2(sum of parallel sides) * h91 = \(\frac{1}{2}\) (5 + 9)h cross multiply 91 = 7h h = \(\frac{91}{7}\) h = 13cm There is an explanation video available below. |
|
| 6. |
Find the value of p if the line which passes through (-1, -p) and (-2,2) is parallel to the line 2y+8x-17=0? A. \(\frac{-2}{7}\) B. \(\frac{7}{6}\) C. \(\frac{-6}{7}\) D. 2 Detailed SolutionLine: 2y+8x-17=0recall y = mx + c 2y = -8x + 17 y = -4x + \(\frac{17}{2}\) Slope m\(_1\) = 4 parallel lines: m\(_1\). m\(_2\) = -4 where Slope ( -4) = \(\frac{y_2 - y_1}{x_2 - x_1}\) at points (-1, -p) and (-2,2) -4( \(x_2 - x_1\) ) = \(y_2 - y_1\) -4 ( -2 - -1) = 2 - -p p = 4 - 2 = 2 There is an explanation video available below. |
|
| 7. |
The ratio of the length of two similar rectangular blocks is 2 : 3. If the volume of the larger block is 351cm\(^3\), then the volume of the other block is? A. 234.00 cm3 B. 526.50 cm3 C. 166.00 cm3 D. 687cm3 Detailed SolutionLet x represent total vol. 2 : 3 = 2 + 3 = 5\(\frac{3}{5}\)x = 351 x = \(\frac{351 \times 5}{3}\) = 585 Volume of smaller block = \(\frac{2}{5}\) x 585 = 234.00cm\(^3\) There is an explanation video available below. |
|
| 8. |
Find the derivative of the function y = 2x\(^2\)(2x - 1) at the point x = -1? A. 18 B. 16 C. -4 D. -6 Detailed Solutiony = 2x\(^2\)(2x - 1) y = 4x\(^3\) - 2x\(^2\) dy/dx = 12x\(^2\) - 4x at x = -1 dy/dx = 12(-1)\(^2\) - 4(-1) = 12 + 4 = 16 There is an explanation video available below. |
Preview displays only 8 out of the 40 Questions