Year :
1999
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
1 - 10 of 43 Questions
| # | Question | Ans |
|---|---|---|
| 1. |
The side of a rhombus is 10cm long, correct to the nearest whole number. Between what limits should the perimeter P lie? A. 39cm ≤ P ≤41cm B. 38cm ≤ P < 42cm C. 38.5 ≤ P ≤ 41.5cm D. 38.5 ≤ P ≤ 40cm Detailed SolutionIf the side = 10 cm, correct to the nearest whole number, thenThe side ranges from 9.5 cm to 10.5 cm. (9.5 \(\leq\) s < 10.5) Perimeter of a rhombus = 4 x side \(\therefore\) 4 x 9.5 \(\leq\) perimeter < 4 x 10.5 = 38 cm \(\leq\) P < 42 cm |
|
| 2. |
Simplify log\(_7\) 8 - log\(_7\) 2 + log\(_7\) 4. A. 0 B. \(2log_7 2\) C. \(3log_7 2\) D. \(4log_7 2\) Detailed Solutionlog\(_7\) 8 - log\(_7\) 2 + log\(_7\) 4= log\(_7\) (8/2 x 4) = log\(_7\) 16 = 4 log\(_7\) 2 |
|
| 3. |
If \(K\sqrt{28}+\sqrt{63}-\sqrt{7}=0\), find K. A. -2 B. -1 C. 1 D. 2 Detailed Solution\(K\sqrt{28}+\sqrt{63}-\sqrt{7}=0\\2K\sqrt{7}+3\sqrt{7}-\sqrt{7}=0\\ 2K\sqrt{7}=-2\sqrt{7}\\ K=\frac{-2\sqrt{7}}{2\sqrt{7}}\\ K=-1\) |
|
| 4. |
From a set \(A = [3, \sqrt{2}, 2\sqrt{3}, \sqrt{9}, \sqrt{7}]\), a number is selected at random. Find the probability that is a rational number A. \(\frac{1}{5}\) B. \(\frac{2}{5}\) C. \(\frac{3}{5}\) D. \(\frac{4}{5}\) Detailed Solution\(A = {3, \sqrt{2}, 2\sqrt{3}, \sqrt{9}, \sqrt{7}}\)n(A) = 5 Let the rational nos = R n(R) = 2 (3, \(\sqrt{9}\)) P(R) = 2/5 |
|
| 5. |
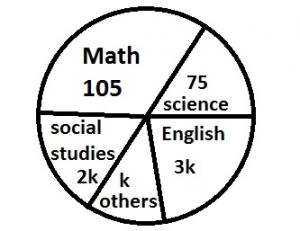 The pie chart illustrate the amount of private time a student spends in a week studying various subjects. use it to answer the question below A. 15o B. 30o C. 60o D. 90o Detailed SolutionTotal angle in a circle = 360°\(\therefore\) 105 + 75 + 2k + k + 3k = 360° 6k = 360 - 180 = 180 k = 180/6 = 30° |
|
| 6. |
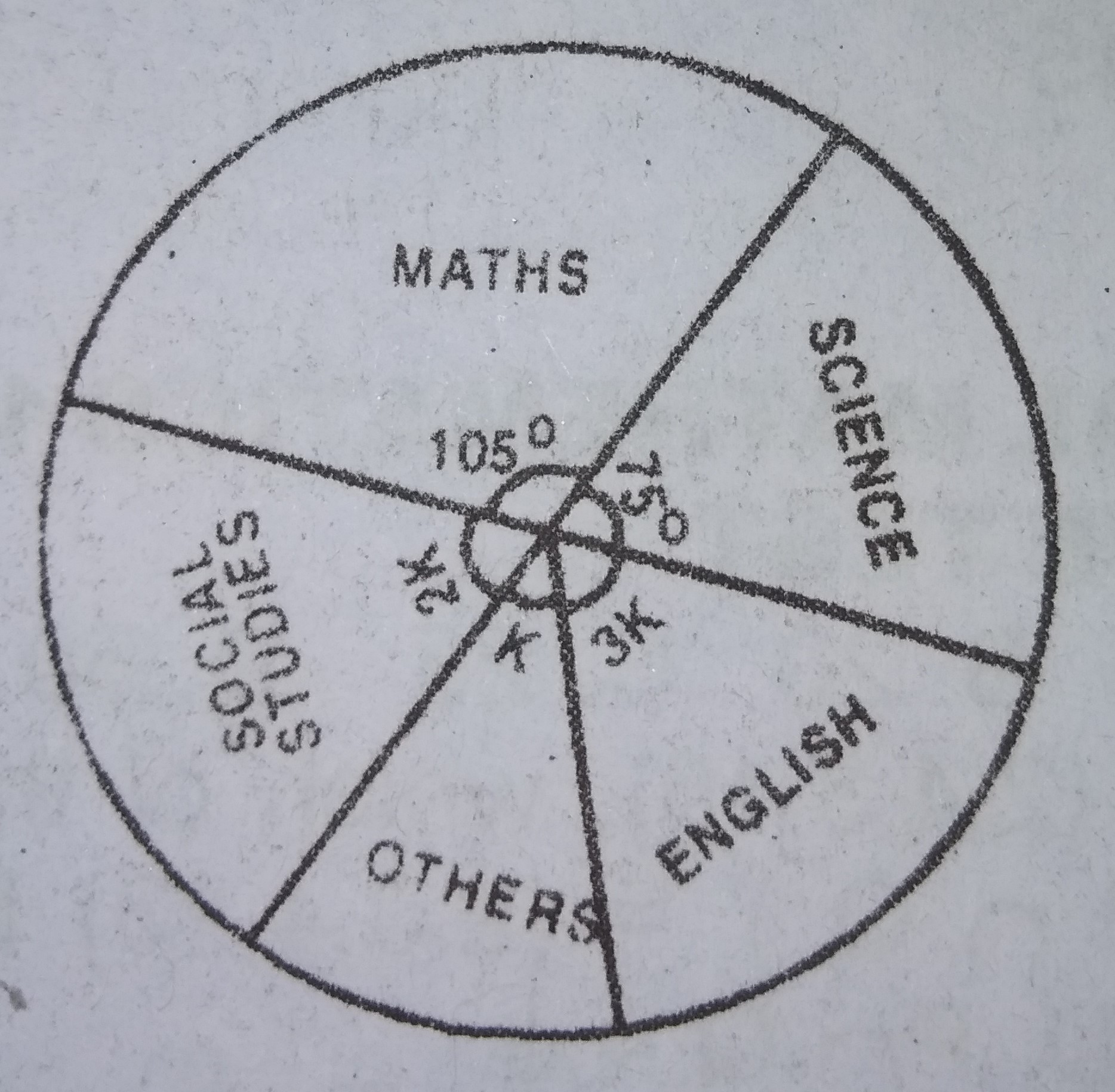 The pie chart illustrate the amount of private time a student spends in a week studying various subjects. use it to answer the question below A. \(3\frac{1}{3}\) hours B. 5 hours C. 8 hours D. 12 hours Detailed SolutionLet x represent the total number of hours spent per week\(∴ \frac{75}{360} \times x = \frac{5}{2}\\ ∴ x = \frac{360 \times 5}{725 \times 2}=12 hours\) |
|
| 7. |
A group of 11 people can speak either English or French or Both. Seven can speak English and six can speak French. What is the probability that a person chosen at random can speak both English and French? A. \(\frac{2}{11}\) B. \(\frac{4}{11}\) C. \(\frac{5}{11}\) D. \(\frac{11}{13}\) Detailed SolutionLet the number of people that speak both English and French = xThen (7 - x) + x + (6 - x) = 11 13 - x = 11 \(\implies\) x = 2. \(\therefore\) P(picking a person that speaks both languages) = 2/11 |
|
| 8. |
The interior angle of a regular polygon is twice the exterior angle. How many sides has the polygon? A. 5 B. 6 C. 8 D. 9 Detailed SolutionLet the exterior angle = dNote: Exterior angle + Interior angle = 180° \(\implies\) d + 2d = 180° 3d = 180° \(\implies\) d = 60° Recall, exterior angle = \(\frac{360}{\text{no of sides}}\) \(\therefore \text{No of sides} = \frac{360}{60}\) = 6 sides |
|
| 9. |
Which of the following figures have one line of symmetry only? I. Isosceles triangle II. Rhombus III. Kite A. I and II only B. II and III only C. I and III only D. I, II, and III Detailed SolutionIsosceles triangle and Kite shapes have 1 line of symmetry each while the rhombus has 2 lines of symmetry. |
|
| 10. |
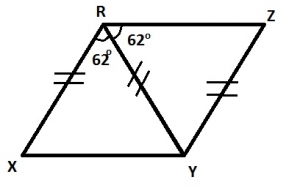 In the diagram above, |XR| = |RY| = |YZ| and ∠XRY = ∠YRZ = 62o, Calculate ∠XYZ A. 50o B. 62o C. 112o D. 115o Detailed SolutionIn triangle RXY, < RXY = < RYX (base angles of an isosceles triangle)\(\implies\) 180° - 62° = 2 < RYX 118° = 2 < RYX \(\implies\) < RYX = 59° In triangle RYZ, < RZY = 62° (base angles of an isosceles triangle) \(\therefore\) < RYZ = 180° - (62° + 62°) = 180° - 124° = 56° \(\therefore\) < XYZ = 56° + 59° = 115° |
| 1. |
The side of a rhombus is 10cm long, correct to the nearest whole number. Between what limits should the perimeter P lie? A. 39cm ≤ P ≤41cm B. 38cm ≤ P < 42cm C. 38.5 ≤ P ≤ 41.5cm D. 38.5 ≤ P ≤ 40cm Detailed SolutionIf the side = 10 cm, correct to the nearest whole number, thenThe side ranges from 9.5 cm to 10.5 cm. (9.5 \(\leq\) s < 10.5) Perimeter of a rhombus = 4 x side \(\therefore\) 4 x 9.5 \(\leq\) perimeter < 4 x 10.5 = 38 cm \(\leq\) P < 42 cm |
|
| 2. |
Simplify log\(_7\) 8 - log\(_7\) 2 + log\(_7\) 4. A. 0 B. \(2log_7 2\) C. \(3log_7 2\) D. \(4log_7 2\) Detailed Solutionlog\(_7\) 8 - log\(_7\) 2 + log\(_7\) 4= log\(_7\) (8/2 x 4) = log\(_7\) 16 = 4 log\(_7\) 2 |
|
| 3. |
If \(K\sqrt{28}+\sqrt{63}-\sqrt{7}=0\), find K. A. -2 B. -1 C. 1 D. 2 Detailed Solution\(K\sqrt{28}+\sqrt{63}-\sqrt{7}=0\\2K\sqrt{7}+3\sqrt{7}-\sqrt{7}=0\\ 2K\sqrt{7}=-2\sqrt{7}\\ K=\frac{-2\sqrt{7}}{2\sqrt{7}}\\ K=-1\) |
|
| 4. |
From a set \(A = [3, \sqrt{2}, 2\sqrt{3}, \sqrt{9}, \sqrt{7}]\), a number is selected at random. Find the probability that is a rational number A. \(\frac{1}{5}\) B. \(\frac{2}{5}\) C. \(\frac{3}{5}\) D. \(\frac{4}{5}\) Detailed Solution\(A = {3, \sqrt{2}, 2\sqrt{3}, \sqrt{9}, \sqrt{7}}\)n(A) = 5 Let the rational nos = R n(R) = 2 (3, \(\sqrt{9}\)) P(R) = 2/5 |
|
| 5. |
 The pie chart illustrate the amount of private time a student spends in a week studying various subjects. use it to answer the question below A. 15o B. 30o C. 60o D. 90o Detailed SolutionTotal angle in a circle = 360°\(\therefore\) 105 + 75 + 2k + k + 3k = 360° 6k = 360 - 180 = 180 k = 180/6 = 30° |
| 6. |
 The pie chart illustrate the amount of private time a student spends in a week studying various subjects. use it to answer the question below A. \(3\frac{1}{3}\) hours B. 5 hours C. 8 hours D. 12 hours Detailed SolutionLet x represent the total number of hours spent per week\(∴ \frac{75}{360} \times x = \frac{5}{2}\\ ∴ x = \frac{360 \times 5}{725 \times 2}=12 hours\) |
|
| 7. |
A group of 11 people can speak either English or French or Both. Seven can speak English and six can speak French. What is the probability that a person chosen at random can speak both English and French? A. \(\frac{2}{11}\) B. \(\frac{4}{11}\) C. \(\frac{5}{11}\) D. \(\frac{11}{13}\) Detailed SolutionLet the number of people that speak both English and French = xThen (7 - x) + x + (6 - x) = 11 13 - x = 11 \(\implies\) x = 2. \(\therefore\) P(picking a person that speaks both languages) = 2/11 |
|
| 8. |
The interior angle of a regular polygon is twice the exterior angle. How many sides has the polygon? A. 5 B. 6 C. 8 D. 9 Detailed SolutionLet the exterior angle = dNote: Exterior angle + Interior angle = 180° \(\implies\) d + 2d = 180° 3d = 180° \(\implies\) d = 60° Recall, exterior angle = \(\frac{360}{\text{no of sides}}\) \(\therefore \text{No of sides} = \frac{360}{60}\) = 6 sides |
|
| 9. |
Which of the following figures have one line of symmetry only? I. Isosceles triangle II. Rhombus III. Kite A. I and II only B. II and III only C. I and III only D. I, II, and III Detailed SolutionIsosceles triangle and Kite shapes have 1 line of symmetry each while the rhombus has 2 lines of symmetry. |
|
| 10. |
 In the diagram above, |XR| = |RY| = |YZ| and ∠XRY = ∠YRZ = 62o, Calculate ∠XYZ A. 50o B. 62o C. 112o D. 115o Detailed SolutionIn triangle RXY, < RXY = < RYX (base angles of an isosceles triangle)\(\implies\) 180° - 62° = 2 < RYX 118° = 2 < RYX \(\implies\) < RYX = 59° In triangle RYZ, < RZY = 62° (base angles of an isosceles triangle) \(\therefore\) < RYZ = 180° - (62° + 62°) = 180° - 124° = 56° \(\therefore\) < XYZ = 56° + 59° = 115° |