Mathematics (Core), 1999, WASSCE/WAEC MAY/JUNE, Exam, Paper 1 | Objectives

Paper Info

Year :

1999

Title :

Mathematics (Core)

Exam :

WASSCE/WAEC MAY/JUNE

Paper 1 | Objectives

31 - 40 of 43 Questions

#	Question	Ans
31.	Amina had m mangoes. She ate 3 and shared the remainder equally with her brother Uche. Each had at least 10. Which of the following inequalities represents the statements above. A. \(\frac{m}{2}-3\le 10\) B. \(\frac{m}{2}-3\ge 10\) C. \(\frac{m-3}{2}\ge10\) D. \(\frac{m-3}{2}\le10\) Show Content Detailed Solution Total number of mangoes = m Amina ate 3 mangoes \(\implies\) Remainder = m - 3 Shared equally with Uche \(\implies \frac{m - 3}{2}\) \(\frac{m - 3}{2} \geq 10\)	C
32.	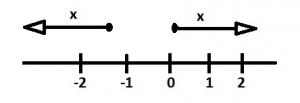Which of the following pairs of inequalities is represented on the number line? A. \(x<-2 and x\ge1\) B. \(x\ge -2 and x>1\) C. \(x\le -2 and x\ge1\) D. \(x< -2 and x>1\)	C
33.	If \(x^2 +15x + 50 = ax^2 + bx + c = 0\). Which of the following statement is not true? A. x = -5 B. x = 10 C. x + 10 = 0 D. bc = 750 Show Content Detailed Solution \(x^2 + 15x + 50 = 0\) \(x^2 + 5x + 10x + 50 = 0\) \(x(x + 5) + 10(x + 5) = 0\) \((x + 5)(x + 10) = 0\) x + 5 = 0 or x + 10 = 0. Comparing \(x^2 + 15x + 50\) with \(ax^2 + bx + c\), b = 15 and c = 50. \(\therefore\) bc = 750.	B
34.	The root of a quadratic equation in x, are -m and 2n. Find the equation A. \(x^2 + x(m - 2n)-2mn=0\) B. \(x^2 - x(m - 2n)-2mn=0\) C. \(x^2 - x(m - 2n)+2mn=0\) D. \(x^2 + x(m - 2n)+2mn=0\) Show Content Detailed Solution x = -m \(\implies\) x + m = 0; x = 2n \(\implies\) x - 2n = 0. \(\implies (x + m)(x - 2n) = 0\) \(x^2 + mx - 2nx - 2mn = 0\) \(x^2 + x(m - 2n) - 2mn = 0\)	A
35.	A survey shows that 28% of all the men in a village wear size 9 shoes. What is the probability that a man selected at random in the village wears size 9 shoes? A. \(\frac{7}{25}\) B. \(\frac{41}{50}\) C. \(\frac{1}{2}\) D. 1 Show Content Detailed Solution P(man picked at random wears size 9 shoes) = \(\frac{28}{100}\) = \(\frac{7}{25}\)	A
36.	Solve the inequality 2x + 3 < 5x A. \(x>1\) B. \(x<\frac{3}{7}\) C. \(x>\frac{3}{7}\) D. \(x>-1\) Show Content Detailed Solution 2x + 3 < 5x -3x < -3 X > 1	A
37.	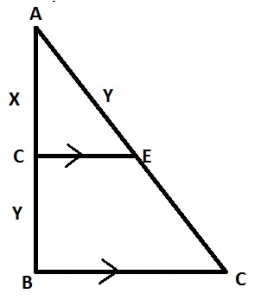In the diagram, DE\|\|BC, \|AD\| = x cm and \|DB\| = \|AE\| = ycm. Find \|CE\| in terms of x and y A. x B. \(\frac{x^2}{y}\) C. \(\frac{y}{x^2}\) D. \(\frac{y^2}{x}\) Show Content Detailed Solution \(\frac{x}{x+y}=\frac{y}{x+CE}\\ xy + xCE = xy + y^2\\ ∴xCE = y^2\\ CE=\frac{y^2}{x}\)	D
38.	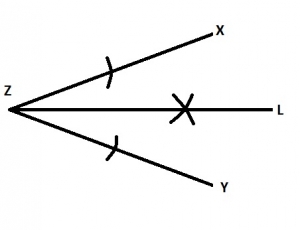Describe the locus L shown in the diagram below A. Locus of points equidistant from X and Y B. Locus of points equidistant from X and Z C. Locus of points equidistant from \(\bar{ZX}\) and \(\bar{ZY}\) D. Locus of points equidistant from \(\bar{XY}\) and \(\bar{ZY}\)	C
39.	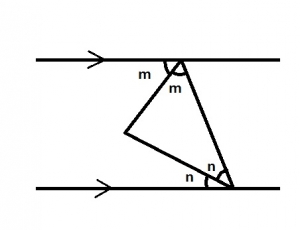Which of the following statements is true from the diagram above? A. m + n = 90^o B. m = n C. n > 45^o D. m < 45^o	A
40.	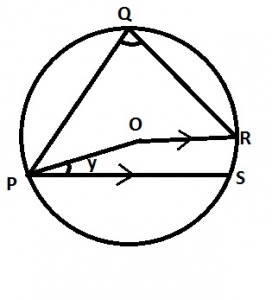In the diagram, O is the centre of the circle ∠PQR = 75^o, ∠OPS = y^o and \(\bar{OR}\) is parallel to \(\bar{PS}\). Find y A. 15 B. 30 C. 45 D. 75	B

31.	Amina had m mangoes. She ate 3 and shared the remainder equally with her brother Uche. Each had at least 10. Which of the following inequalities represents the statements above. A. \(\frac{m}{2}-3\le 10\) B. \(\frac{m}{2}-3\ge 10\) C. \(\frac{m-3}{2}\ge10\) D. \(\frac{m-3}{2}\le10\) Show Content Detailed Solution Total number of mangoes = m Amina ate 3 mangoes \(\implies\) Remainder = m - 3 Shared equally with Uche \(\implies \frac{m - 3}{2}\) \(\frac{m - 3}{2} \geq 10\)	C
32.	Which of the following pairs of inequalities is represented on the number line? A. \(x<-2 and x\ge1\) B. \(x\ge -2 and x>1\) C. \(x\le -2 and x\ge1\) D. \(x< -2 and x>1\)	C
33.	If \(x^2 +15x + 50 = ax^2 + bx + c = 0\). Which of the following statement is not true? A. x = -5 B. x = 10 C. x + 10 = 0 D. bc = 750 Show Content Detailed Solution \(x^2 + 15x + 50 = 0\) \(x^2 + 5x + 10x + 50 = 0\) \(x(x + 5) + 10(x + 5) = 0\) \((x + 5)(x + 10) = 0\) x + 5 = 0 or x + 10 = 0. Comparing \(x^2 + 15x + 50\) with \(ax^2 + bx + c\), b = 15 and c = 50. \(\therefore\) bc = 750.	B
34.	The root of a quadratic equation in x, are -m and 2n. Find the equation A. \(x^2 + x(m - 2n)-2mn=0\) B. \(x^2 - x(m - 2n)-2mn=0\) C. \(x^2 - x(m - 2n)+2mn=0\) D. \(x^2 + x(m - 2n)+2mn=0\) Show Content Detailed Solution x = -m \(\implies\) x + m = 0; x = 2n \(\implies\) x - 2n = 0. \(\implies (x + m)(x - 2n) = 0\) \(x^2 + mx - 2nx - 2mn = 0\) \(x^2 + x(m - 2n) - 2mn = 0\)	A
35.	A survey shows that 28% of all the men in a village wear size 9 shoes. What is the probability that a man selected at random in the village wears size 9 shoes? A. \(\frac{7}{25}\) B. \(\frac{41}{50}\) C. \(\frac{1}{2}\) D. 1 Show Content Detailed Solution P(man picked at random wears size 9 shoes) = \(\frac{28}{100}\) = \(\frac{7}{25}\)	A

36.	Solve the inequality 2x + 3 < 5x A. \(x>1\) B. \(x<\frac{3}{7}\) C. \(x>\frac{3}{7}\) D. \(x>-1\) Show Content Detailed Solution 2x + 3 < 5x -3x < -3 X > 1	A
37.	In the diagram, DE\|\|BC, \|AD\| = x cm and \|DB\| = \|AE\| = ycm. Find \|CE\| in terms of x and y A. x B. \(\frac{x^2}{y}\) C. \(\frac{y}{x^2}\) D. \(\frac{y^2}{x}\) Show Content Detailed Solution \(\frac{x}{x+y}=\frac{y}{x+CE}\\ xy + xCE = xy + y^2\\ ∴xCE = y^2\\ CE=\frac{y^2}{x}\)	D
38.	Describe the locus L shown in the diagram below A. Locus of points equidistant from X and Y B. Locus of points equidistant from X and Z C. Locus of points equidistant from \(\bar{ZX}\) and \(\bar{ZY}\) D. Locus of points equidistant from \(\bar{XY}\) and \(\bar{ZY}\)	C
39.	Which of the following statements is true from the diagram above? A. m + n = 90^o B. m = n C. n > 45^o D. m < 45^o	A
40.	In the diagram, O is the centre of the circle ∠PQR = 75^o, ∠OPS = y^o and \(\bar{OR}\) is parallel to \(\bar{PS}\). Find y A. 15 B. 30 C. 45 D. 75	B