Year :
2003
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 45 of 45 Questions
| # | Question | Ans | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 41. |
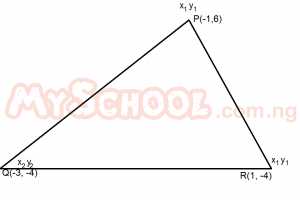
A triangle has vertices P(-1,6), Q(-3, -4) and R(1, -4).Find the midpoint of PQ and QR respectively. A. (0,-2) and (-1, -4) B. (-1,0) and (-1,-1) C. (-2,1) and (0,1) D. (-2,1) and (-1,-4) Detailed Solution
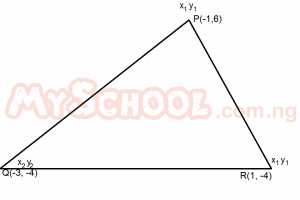 =\frac{-1+(-3)}{2};\frac{6-4}{2}\\ =\frac{-4}{2};\frac{2}{2}\\ =-2,1\) Midpoint of QR = \(\frac{x_2 + x_1}{2};\frac{y_2 + y_1}{2}\\ \frac{-3+1}{2};\frac{-4-4}{2}\\ \frac{-2}{2};\frac{-8}{2}\\ -1,-4\) Midpoint of PQ and QR = (-2,1) and (-1,-4) |
|||||||||||||||
| 42. |
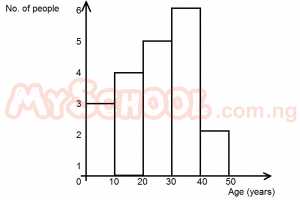 The histogram above shows the ages of the victims of a pollution. How many people were involved in the pollution? A. 15 B. 18 C. 20 D. 21 Detailed Solution
|
|||||||||||||||
| 43. |
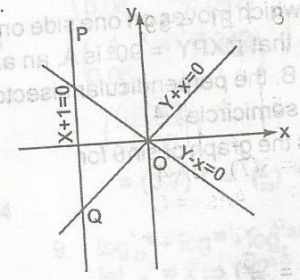 Triangle OPQ is the solution of the inequalities A. x - 1 < 0, y + \(\geq\) 0, y - x \(\geq\) 0 B. x + 1 \(\leq\) 0, y + x \(\geq\) 0, y - x \(\leq\) 0 C. x - 1 \(\geq\) 0, y - x \(\geq\) 0, y + x \(\geq\) 0 D. y + x \(\geq\) 0, y - x \(\leq\) 0 |
B |
||||||||||||||
| 44. |
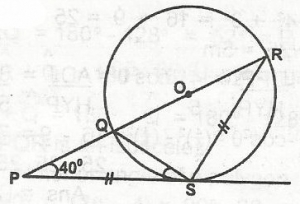 In the diagram PQR is a straight line and PS is a tangent to the circle < QRS with |PS| = |SR| and < SPR = 40°. Find PSQ A. 20o B. 40o C. 10o D. 30o Detailed SolutionPS = SR\(\bigtriangleup\)PSR is an isosceles < P = < SPQ = 40° < R = < SRQ < PSQ = < SRQ (alternate segment) < PSQ = 40° |
|||||||||||||||
| 45. |
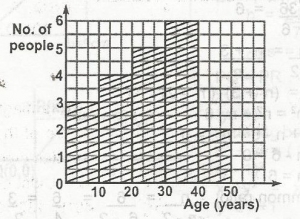 The histogram above shows the ages of victims of a pollution. How many people were involved in the pollution? A. 20 B. 21 C. 15 D. 18 Detailed Solution\(\begin{array}{c|c} \text{Age in years} & 10 & 20 & 30 & 40 & 50 \\\hline \text{frequency} & 3 & 4 & 5 & 6 & 2\end{array}\)\(\sum f \) = number of people involved in the pollution \(\sum f\) = 3 + 4 + 5 + 6 + 2 = 20 |
| 41. |
A triangle has vertices P(-1,6), Q(-3, -4) and R(1, -4).Find the midpoint of PQ and QR respectively. A. (0,-2) and (-1, -4) B. (-1,0) and (-1,-1) C. (-2,1) and (0,1) D. (-2,1) and (-1,-4) Detailed Solution
 =\frac{-1+(-3)}{2};\frac{6-4}{2}\\ =\frac{-4}{2};\frac{2}{2}\\ =-2,1\) Midpoint of QR = \(\frac{x_2 + x_1}{2};\frac{y_2 + y_1}{2}\\ \frac{-3+1}{2};\frac{-4-4}{2}\\ \frac{-2}{2};\frac{-8}{2}\\ -1,-4\) Midpoint of PQ and QR = (-2,1) and (-1,-4) |
|||||||||||||||
| 42. |
 The histogram above shows the ages of the victims of a pollution. How many people were involved in the pollution? A. 15 B. 18 C. 20 D. 21 Detailed Solution
|
|||||||||||||||
| 43. |
 Triangle OPQ is the solution of the inequalities A. x - 1 < 0, y + \(\geq\) 0, y - x \(\geq\) 0 B. x + 1 \(\leq\) 0, y + x \(\geq\) 0, y - x \(\leq\) 0 C. x - 1 \(\geq\) 0, y - x \(\geq\) 0, y + x \(\geq\) 0 D. y + x \(\geq\) 0, y - x \(\leq\) 0 |
B |
| 44. |
 In the diagram PQR is a straight line and PS is a tangent to the circle < QRS with |PS| = |SR| and < SPR = 40°. Find PSQ A. 20o B. 40o C. 10o D. 30o Detailed SolutionPS = SR\(\bigtriangleup\)PSR is an isosceles < P = < SPQ = 40° < R = < SRQ < PSQ = < SRQ (alternate segment) < PSQ = 40° |
|
| 45. |
 The histogram above shows the ages of victims of a pollution. How many people were involved in the pollution? A. 20 B. 21 C. 15 D. 18 Detailed Solution\(\begin{array}{c|c} \text{Age in years} & 10 & 20 & 30 & 40 & 50 \\\hline \text{frequency} & 3 & 4 & 5 & 6 & 2\end{array}\)\(\sum f \) = number of people involved in the pollution \(\sum f\) = 3 + 4 + 5 + 6 + 2 = 20 |