Year : 
2003
Title : 
Mathematics (Core)
Exam : 
JAMB Exam

Paper 1 | Objectives

31 - 40 of 45 Questions

# Question Ans
31.

If \(^{n}P_{3} - 6(^{n}C_{4}) = 0\), find the value of n.

A. 5

B. 6

C. 7

D. 8

Detailed Solution

\(^{n}P_3 - 6(^{n}C_{4})=0\\\frac{n!}{(n-3)!}-6\left( \frac{n!}{(n-4)!4!}\right)=0\\\frac{n!}{(n-3)!}=6\left(\frac{n!}{(n-4)!4!}\right)\\n!((n-4)!4!)=6n!(n-3)!\\((n-4)!4!)=6(n-3)!\\\frac{(n-4)!}{(n-3)!}=\frac{6}{4!}\\\frac{(n-4)!}{(n-3)(n-4)!}=\frac{6}{4 \times 3\times 2\times 1}\\\frac{1}{(n-3)}=]\frac{1}{4}\\n-3=4\\n=4+3\\n=7\)
32.

Find the number of committees of three that can be formed consisting of two men and one woman from four men and three women

A. 3

B. 6

C. 18

D. 24

Detailed Solution

\(^{4}C_2 \times ^{3}C_1 = \left(\frac{4!}{(4-2)!2!}\right)\times\left(\frac{3!}{(3-1)!1!}\right)\\=\frac{4!}{2!2!}\times \frac{3!}{2!}\\=\frac{4 \times 3 \times 2!}{2 \times 1 \times 2!} \times \frac{3 \times 2!}{2!}\\=18\)
33.

A bag contains 5 blacks balls and 3 red balls. Two balls are picked at random without replacement. What is the probability that a black and red balls are picked?

A. 15/28

B. 13/28

C. 5/14

D. 3/14

Detailed Solution

Black balls = 5
Red balls = 3/8
P(B) = 5/8, P(R) = 3/8
P( a Black and a Red) = BR + RB
= (5/8) * (3/7) * (3/8) * (5/7)
= (15/56) + (15/56)
= 30/56
= 15/28
34.

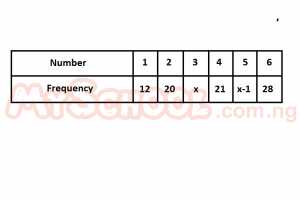The result of tossing a fair die 120 times is summarized above. Find the value of x

A. 19

B. 20

C. 21

D. 22

Detailed Solution

12 + 20 + x + 21 + x-1 +28 = 120
2x + 80 = 120
2x = 120 - 80
2x = 40
x = 20
35.

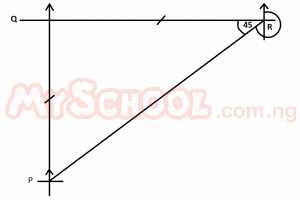
An aeroplane flies due north from airport P to Q and then flies due east R. If Q is equidistant from P and R, find the bearing of P and R

A. 90o

B. 135o

C. 225o

D. 270o

Detailed Solution

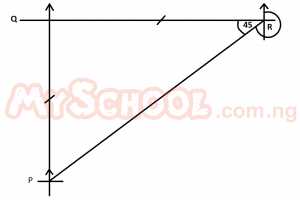Since PQ = QR, Δ PQR is a right angle isosceles triangle
∴ ∠PQR = 45o
=> The bearing of P from R = 180 + 45
= 225o
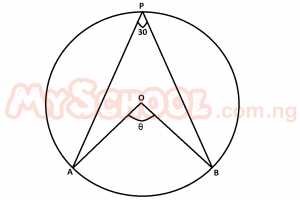
36.

An arc of a circle subtends an angle of 30° on the circumference of a circle of radius 21cm. Find the length of the arc.

A. 11cm

B. 22cm

C. 44cm

D. 66cm

Detailed Solution

θ = 30 x 2(∠ at center twice ∠ at θ)
∴ θ = 60°
Length of arc = \(\frac{\theta}{360}\times 2\pi r\\
=\frac{60}{360}\times 2 \times \frac{22}{7}\times \frac{21}{1}\\
=22cm\)
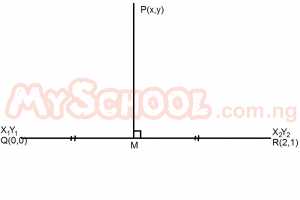
37.

Find the equation of the locus of a point P(x,y) which is equidistant from Q(0,0) and R(2,1).

A. 4x + 2y = 5

B. 4x - 2y = 5

C. 2x + 2y = 5

D. 2x + y = 5

Detailed Solution

Locus of a point P(x,y) which is equidistant from Q(0,0) and R(2,1) is the perpendicular bisector of the straight line joining Q and R
Mid point QR = \(\frac{x_2 + x_1}{2}, \frac{y_2 + y_1}{2}\)
= \(\frac{2 + 0}{2}, \frac{1 + 0}{2}\)
= \((1, \frac{1}{2})\)
Gradient of QR = \(\frac{y_{2} - y_{1}}{x_{2} - x_{1}}\)
= \(\frac{1 - 0}{2 - 0}\)
= \(\frac{1}{2}\)
Gradient of PM = \(\frac{-1}{\frac{1}{2}}\)
= -2
Equation of PM = y - y\(_1\) = m(x-x_\(_1\))
i.e y - 1/2 = -2(x-1)
2y - 1 = -4(x-1)
2y - 1 = -4x + 4
2y + 4x = 5
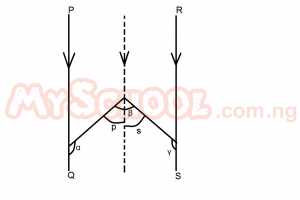
38.

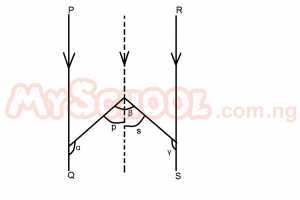In the diagram above, PQ is parallel to RS. What is the value of α + β + γ?

A. 360o

B. 200o

C. 180o

D. 90o

Detailed Solution

γ + S = 180(Allied angles)
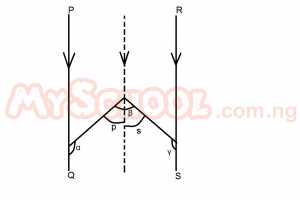S = 180 - γ
α + P = 180(Allied angles)
p = 180 - α
β = P + S
β = 180 - α + 180 - γ
β = 360 - α - γ
β + α + γ = 360
39.

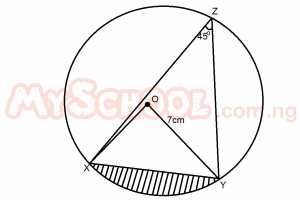
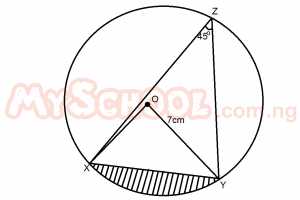XYZ is a circle with center O and a radius 7cm. Find the area of the shaded region.

A. 84cm2

B. 77cm2

C. 38cm2

D. 14cm2

Detailed Solution

θ = 45 x 2 (∠ at center twice ∠ at θ)
θ = 90°
Area of sector = θ/360 x πr2
= 90/360 x 22/7 x 7 x 7
= 77/2cm\(^2\)
Area of triangle = 1/2 ab sin θ
= 1/2 x 7 x 7 sin 90
= 1/2 x 7 x 7 x 1
= 49/2 cm\(^{2}\)
Area of shaded region = 77/2 - 49/2
= 28/2
= 14cm\(^2\)
40.

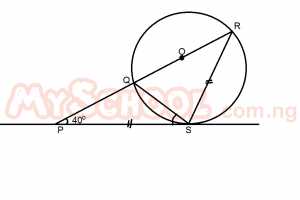
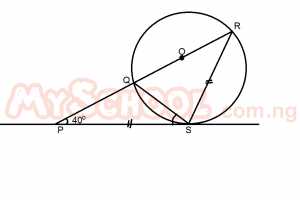In the diagram above, PQR is a straight line and PS is a tangent to the circle QRS with /PS/ = /SR/ and ∠SPR = 40°. Find ∠PSQ

A. 40o

B. 30o

C. 20o

D. 10o

Detailed Solution

R = P (base ∠s of isc Δ, ps = RS)
∴R = 40°
∠PSQ = R (∠s in alternate segment)
∴∠PSQ = 40°
31.

If \(^{n}P_{3} - 6(^{n}C_{4}) = 0\), find the value of n.

A. 5

B. 6

C. 7

D. 8

Detailed Solution

\(^{n}P_3 - 6(^{n}C_{4})=0\\\frac{n!}{(n-3)!}-6\left( \frac{n!}{(n-4)!4!}\right)=0\\\frac{n!}{(n-3)!}=6\left(\frac{n!}{(n-4)!4!}\right)\\n!((n-4)!4!)=6n!(n-3)!\\((n-4)!4!)=6(n-3)!\\\frac{(n-4)!}{(n-3)!}=\frac{6}{4!}\\\frac{(n-4)!}{(n-3)(n-4)!}=\frac{6}{4 \times 3\times 2\times 1}\\\frac{1}{(n-3)}=]\frac{1}{4}\\n-3=4\\n=4+3\\n=7\)
32.

Find the number of committees of three that can be formed consisting of two men and one woman from four men and three women

A. 3

B. 6

C. 18

D. 24

Detailed Solution

\(^{4}C_2 \times ^{3}C_1 = \left(\frac{4!}{(4-2)!2!}\right)\times\left(\frac{3!}{(3-1)!1!}\right)\\=\frac{4!}{2!2!}\times \frac{3!}{2!}\\=\frac{4 \times 3 \times 2!}{2 \times 1 \times 2!} \times \frac{3 \times 2!}{2!}\\=18\)
33.

A bag contains 5 blacks balls and 3 red balls. Two balls are picked at random without replacement. What is the probability that a black and red balls are picked?

A. 15/28

B. 13/28

C. 5/14

D. 3/14

Detailed Solution

Black balls = 5
Red balls = 3/8
P(B) = 5/8, P(R) = 3/8
P( a Black and a Red) = BR + RB
= (5/8) * (3/7) * (3/8) * (5/7)
= (15/56) + (15/56)
= 30/56
= 15/28
34.

The result of tossing a fair die 120 times is summarized above. Find the value of x

A. 19

B. 20

C. 21

D. 22

Detailed Solution

12 + 20 + x + 21 + x-1 +28 = 120
2x + 80 = 120
2x = 120 - 80
2x = 40
x = 20
35.

An aeroplane flies due north from airport P to Q and then flies due east R. If Q is equidistant from P and R, find the bearing of P and R

A. 90o

B. 135o

C. 225o

D. 270o

Detailed Solution

Since PQ = QR, Δ PQR is a right angle isosceles triangle
∴ ∠PQR = 45o
=> The bearing of P from R = 180 + 45
= 225o
36.

An arc of a circle subtends an angle of 30° on the circumference of a circle of radius 21cm. Find the length of the arc.

A. 11cm

B. 22cm

C. 44cm

D. 66cm

Detailed Solution

θ = 30 x 2(∠ at center twice ∠ at θ)
∴ θ = 60°
Length of arc = \(\frac{\theta}{360}\times 2\pi r\\
=\frac{60}{360}\times 2 \times \frac{22}{7}\times \frac{21}{1}\\
=22cm\)
37.

Find the equation of the locus of a point P(x,y) which is equidistant from Q(0,0) and R(2,1).

A. 4x + 2y = 5

B. 4x - 2y = 5

C. 2x + 2y = 5

D. 2x + y = 5

Detailed Solution

Locus of a point P(x,y) which is equidistant from Q(0,0) and R(2,1) is the perpendicular bisector of the straight line joining Q and R
Mid point QR = \(\frac{x_2 + x_1}{2}, \frac{y_2 + y_1}{2}\)
= \(\frac{2 + 0}{2}, \frac{1 + 0}{2}\)
= \((1, \frac{1}{2})\)
Gradient of QR = \(\frac{y_{2} - y_{1}}{x_{2} - x_{1}}\)
= \(\frac{1 - 0}{2 - 0}\)
= \(\frac{1}{2}\)
Gradient of PM = \(\frac{-1}{\frac{1}{2}}\)
= -2
Equation of PM = y - y\(_1\) = m(x-x_\(_1\))
i.e y - 1/2 = -2(x-1)
2y - 1 = -4(x-1)
2y - 1 = -4x + 4
2y + 4x = 5
38.

In the diagram above, PQ is parallel to RS. What is the value of α + β + γ?

A. 360o

B. 200o

C. 180o

D. 90o

Detailed Solution

γ + S = 180(Allied angles)
S = 180 - γ
α + P = 180(Allied angles)
p = 180 - α
β = P + S
β = 180 - α + 180 - γ
β = 360 - α - γ
β + α + γ = 360
39.

XYZ is a circle with center O and a radius 7cm. Find the area of the shaded region.

A. 84cm2

B. 77cm2

C. 38cm2

D. 14cm2

Detailed Solution

θ = 45 x 2 (∠ at center twice ∠ at θ)
θ = 90°
Area of sector = θ/360 x πr2
= 90/360 x 22/7 x 7 x 7
= 77/2cm\(^2\)
Area of triangle = 1/2 ab sin θ
= 1/2 x 7 x 7 sin 90
= 1/2 x 7 x 7 x 1
= 49/2 cm\(^{2}\)
Area of shaded region = 77/2 - 49/2
= 28/2
= 14cm\(^2\)
40.

In the diagram above, PQR is a straight line and PS is a tangent to the circle QRS with /PS/ = /SR/ and ∠SPR = 40°. Find ∠PSQ

A. 40o

B. 30o

C. 20o

D. 10o

Detailed Solution

R = P (base ∠s of isc Δ, ps = RS)
∴R = 40°
∠PSQ = R (∠s in alternate segment)
∴∠PSQ = 40°