Year :
2003
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
21 - 30 of 45 Questions
| # | Question | Ans |
|---|---|---|
| 21. |
A trapezium has two parallel sides of length 5cm and 9cm. If the area is 21cm2, find the distance between the parallel sides A. 3 cm B. 4 cm C. 6 cm D. 7 cm Detailed SolutionArea of Trapezium = 1/2(sum of parralel sides) * ht21 = 1/2(5 + 9)h 42 = 14h h = 42/14 h = 3cm |
|
| 22. |
The locus of a point P which moves on one side only of a straight line XY so that ∠XPY = 90o is A. a circle B. a semicircle C. an arc of a circle through X, Y D. the perpendicular bisector of XY |
B |
| 23. |
Find the slope of the curve y = 2x\(^2\) + 5x - 3 at (1, 4). A. 4 B. 6 C. 7 D. 9 Detailed Solutiony = 2x\(^2\) + 5x - 3dy/dx = 4x + 5 = 4 + 5 = 9 |
|
| 24. |
Evaluate \(\int^{2} _{3}(x^2 - 2x)dx\) A. 4 B. 2 C. 4/3 D. 1/3 Detailed Solution\(\int^{2} _{3}(x^2 - 2x)dx\\=\left[\frac{x^3}{3}-\frac{2x^2}{2}\right ]^{2}_{3}\\\left[\frac{x^3}{3}-x^2 + C\right ]^{2}_{3}\\\left[\frac{3^3}{3}-3^2 + C \right ]-\left[\frac{2^3}{3}-2^2 + C \right ]\\9-9-\left[\frac{8}{3}-4 \right ]\\=\frac{-8}{3}+4\\=\frac{4}{3}\) |
|
| 25. |
If y = 3 sin(-4x), dy/dx is A. 12x cos (4x) B. -12x cos (-4x) C. -12 cos (-4x) D. 12 sin (-4x) Detailed Solutiony = 3 sin(-4x)dy/dx = 3 x - 4 cos (-4x) = -12 cos (-4x) |
|
| 26. |
Determine the maximum value of y = 3x2 - x3 A. zero B. 2 C. 4 D. 6 Detailed Solutiony = 3x2 - x3dy/dx = 6x - 3x2 as dy/dx = 0 6x - 3x2 = 0 3x (2 - x) = 0 this implies that 2 -x = 0 and 3x = 0 x = 2 (or) 0 But = dy/dx = 6x - 3x2 d2y/dx2 = 6 - 6x at x = 2 = 6 - 6(2) = -6 y = 3x2 - x3 = 3(2)2 - 23 = 12 - 8 = 4 |
|
| 27. |
By how much is the mean of 30, 56, 31, 55, 43 and 44 less than the median? A. 0.75 B. 0.50 C. 0.33 D. 0.17 Detailed Solution\(Mean = \frac{30+56+31+55+43+44}{6}\\=\frac{259}{6}=43.167\\Median = 30,31,43,44,55,56\\=\frac{43+44}{2}=\frac{87}{2}=43.5\\Median-mean = 43.5-43.17=0.33\) |
|
| 28. |
The range of 4, 3, 11, 9, 6, 15, 19, 23, 27, 24,21 and 16 is A. 16 B. 21 C. 23 D. 24 Detailed SolutionRange = (Highest - Lowest) items= 27 - 3 = 24 |
|
| 29. |
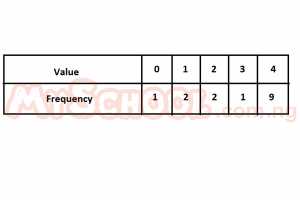 Find the mean of the distribution above A. 1 B. 2 C. 3 D. 4 Detailed Solution\(Mean = \frac{(0 \times 1) + (1 \times 2) + (2 \times 2) + (3 \times 1) + (4 \times 9)}{1 + 2 + 2 + 1 + 9}\\=\frac{(0 + 2 + 4 + 3 + 36)}{15}\\=\frac{45}{15}=3\) |
|
| 30. |
On a pie chart, there are four sectors of which three angles are 45°, 90° and 135°. If the smallest sector represents N28.00, how much is the largest sector? A. N96.00 B. N84.00 C. N48.00 D. N42.00 Detailed SolutionLet the 4th angle be = x∴ x + 45 + 90 + 135 = 360 x + 270 = 360 x = 360 - 270 x = 90 ∴ smallest angle = 45o 45o = N28.00 1o = 28.00/45 135o = (28.00/45) * (135/1) = N84.00 |
| 21. |
A trapezium has two parallel sides of length 5cm and 9cm. If the area is 21cm2, find the distance between the parallel sides A. 3 cm B. 4 cm C. 6 cm D. 7 cm Detailed SolutionArea of Trapezium = 1/2(sum of parralel sides) * ht21 = 1/2(5 + 9)h 42 = 14h h = 42/14 h = 3cm |
|
| 22. |
The locus of a point P which moves on one side only of a straight line XY so that ∠XPY = 90o is A. a circle B. a semicircle C. an arc of a circle through X, Y D. the perpendicular bisector of XY |
B |
| 23. |
Find the slope of the curve y = 2x\(^2\) + 5x - 3 at (1, 4). A. 4 B. 6 C. 7 D. 9 Detailed Solutiony = 2x\(^2\) + 5x - 3dy/dx = 4x + 5 = 4 + 5 = 9 |
|
| 24. |
Evaluate \(\int^{2} _{3}(x^2 - 2x)dx\) A. 4 B. 2 C. 4/3 D. 1/3 Detailed Solution\(\int^{2} _{3}(x^2 - 2x)dx\\=\left[\frac{x^3}{3}-\frac{2x^2}{2}\right ]^{2}_{3}\\\left[\frac{x^3}{3}-x^2 + C\right ]^{2}_{3}\\\left[\frac{3^3}{3}-3^2 + C \right ]-\left[\frac{2^3}{3}-2^2 + C \right ]\\9-9-\left[\frac{8}{3}-4 \right ]\\=\frac{-8}{3}+4\\=\frac{4}{3}\) |
|
| 25. |
If y = 3 sin(-4x), dy/dx is A. 12x cos (4x) B. -12x cos (-4x) C. -12 cos (-4x) D. 12 sin (-4x) Detailed Solutiony = 3 sin(-4x)dy/dx = 3 x - 4 cos (-4x) = -12 cos (-4x) |
| 26. |
Determine the maximum value of y = 3x2 - x3 A. zero B. 2 C. 4 D. 6 Detailed Solutiony = 3x2 - x3dy/dx = 6x - 3x2 as dy/dx = 0 6x - 3x2 = 0 3x (2 - x) = 0 this implies that 2 -x = 0 and 3x = 0 x = 2 (or) 0 But = dy/dx = 6x - 3x2 d2y/dx2 = 6 - 6x at x = 2 = 6 - 6(2) = -6 y = 3x2 - x3 = 3(2)2 - 23 = 12 - 8 = 4 |
|
| 27. |
By how much is the mean of 30, 56, 31, 55, 43 and 44 less than the median? A. 0.75 B. 0.50 C. 0.33 D. 0.17 Detailed Solution\(Mean = \frac{30+56+31+55+43+44}{6}\\=\frac{259}{6}=43.167\\Median = 30,31,43,44,55,56\\=\frac{43+44}{2}=\frac{87}{2}=43.5\\Median-mean = 43.5-43.17=0.33\) |
|
| 28. |
The range of 4, 3, 11, 9, 6, 15, 19, 23, 27, 24,21 and 16 is A. 16 B. 21 C. 23 D. 24 Detailed SolutionRange = (Highest - Lowest) items= 27 - 3 = 24 |
|
| 29. |
 Find the mean of the distribution above A. 1 B. 2 C. 3 D. 4 Detailed Solution\(Mean = \frac{(0 \times 1) + (1 \times 2) + (2 \times 2) + (3 \times 1) + (4 \times 9)}{1 + 2 + 2 + 1 + 9}\\=\frac{(0 + 2 + 4 + 3 + 36)}{15}\\=\frac{45}{15}=3\) |
|
| 30. |
On a pie chart, there are four sectors of which three angles are 45°, 90° and 135°. If the smallest sector represents N28.00, how much is the largest sector? A. N96.00 B. N84.00 C. N48.00 D. N42.00 Detailed SolutionLet the 4th angle be = x∴ x + 45 + 90 + 135 = 360 x + 270 = 360 x = 360 - 270 x = 90 ∴ smallest angle = 45o 45o = N28.00 1o = 28.00/45 135o = (28.00/45) * (135/1) = N84.00 |