Mathematics (Core), 2007, WASSCE/WAEC MAY/JUNE, Exam, Paper 1 | Objectives

Paper Info

Year :

2007

Title :

Mathematics (Core)

Exam :

WASSCE/WAEC MAY/JUNE

Paper 1 | Objectives

61 - 67 of 67 Questions

#	Question	Ans
61.	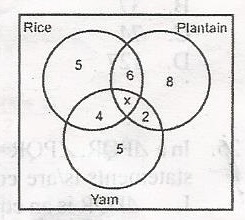The venn diagram shows the choice of food of a number of visitors to a canteen. How many people took at least two kinds of food? A. 10 B. 12 C. 15 D. 17 Show Content Detailed Solution at least 2 kinds of food two or more foods i.e(R and p) + (p and Y) + (y and R) + R and y and p = 6 + 2 + 4 + 5 = 17	D
62.	If the ratio x:y = 3:5 and y:z = 4:7, find the ratio x:y:z A. 15 : 28 : 84 B. 12 : 20 : 35 C. 3 : 5 : 4 D. 5 : 4 : 7 Show Content Detailed Solution x : y = 3.5, y : z = 4 : 7 x = 3 x 4 = 12 y = 5 x 4 = 20 y = 4 x 5 = 20 z = 7 x 5 = 35 then x : y : z = 12 : 20 : 35	B
63.	In the diagram, O is the centre of the circle and < PQR = 106^o, find the value of y A. 16 B. 37 C. 74 D. 127 Show Content Detailed Solution 2y + Reflex angle = 360 Reflex angle = 360 - 2y 360 - 2y = 2(106)(angles at a centre = 2ce < of circum.) 360 - 212 = 2y 148 = 2y y \(\frac{148}{2}\) y = 74^o	C
64.	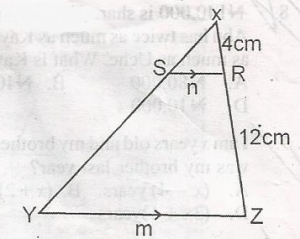In the diagram, \|XR\| = 4cm \|RZ\| = 12cm, \|SR\| = n, \|XZ\| = m and SR\|\|YZ. Find m in terms of n A. m = 2n B. m = 3n C. m = 4n D. m = 5n Show Content Detailed Solution \(\frac{n}{4} = \frac{m}{4 + 12}\) \(\frac{n}{4} = \frac{m}{16}\) 4m = 16n \(\frac{4m}{4} = \frac{16n}{4}\) m = 4n	C
65.	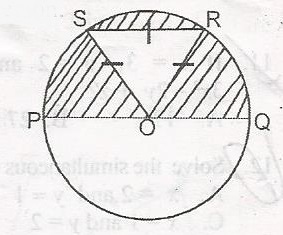In the diagram, O is the centre of the circle and PQ is a diameter. Triangle RSO is an equilateral triangle of side 4cm. Find the area of the shaded region A. 43.36cm² B. 32.07² C. 18.21² D. 6.93² Show Content Detailed Solution Area of shaded portion = Area of semicircle Area of \(\bigtriangleup\) RSO Area of semicircle = \(\frac {\pi r^2}{2} = \frac{22\times 4 \times 4}{7 \times 3}\) = 25.14cm²; Area of \(\bigtriangleup\)RSO =\(\sqrt{s(s - 1)(s - b)(s - c)}\); where s = \(\frac{a + b + c}{2}\) s = \(\frac{4 + 4 + 4}{2}\) = 6cm = \(\sqrt{6(6 - 4)(6 - 4) (6 - 4)}\) = \(\sqrt{6(2) (2) (2)}\) = \(\sqrt{18}\) = 6.93cm² Area of shaded region = 25.14 - 6.93 &	C
66.	Find the product of 0.0409 and 0.0021 leaving your answer in the standard form A. 8.6 x 10^-6 B. 8.6 x 10⁵ C. 8.6 x 10^-4 D. 8.6 x 10⁵ Show Content Detailed Solution 0.0409 x 0.0021 = 409 x 10^-4 x 21 x 10^-4 = 409 x 21 x 10^-4-4 = 8589 x 10^-8 = 8.589 x 10³ x 10^-8 = 8.6 x 10^{3 - 8} = 8.6 x 10^-5	B
67.	Convert 42₅ to base three numeral A. 201₃ B. 210₃ C. 211₃ D. 343₃	C

61.	The venn diagram shows the choice of food of a number of visitors to a canteen. How many people took at least two kinds of food? A. 10 B. 12 C. 15 D. 17 Show Content Detailed Solution at least 2 kinds of food two or more foods i.e(R and p) + (p and Y) + (y and R) + R and y and p = 6 + 2 + 4 + 5 = 17	D
62.	If the ratio x:y = 3:5 and y:z = 4:7, find the ratio x:y:z A. 15 : 28 : 84 B. 12 : 20 : 35 C. 3 : 5 : 4 D. 5 : 4 : 7 Show Content Detailed Solution x : y = 3.5, y : z = 4 : 7 x = 3 x 4 = 12 y = 5 x 4 = 20 y = 4 x 5 = 20 z = 7 x 5 = 35 then x : y : z = 12 : 20 : 35	B
63.	In the diagram, O is the centre of the circle and < PQR = 106^o, find the value of y A. 16 B. 37 C. 74 D. 127 Show Content Detailed Solution 2y + Reflex angle = 360 Reflex angle = 360 - 2y 360 - 2y = 2(106)(angles at a centre = 2ce < of circum.) 360 - 212 = 2y 148 = 2y y \(\frac{148}{2}\) y = 74^o	C
64.	In the diagram, \|XR\| = 4cm \|RZ\| = 12cm, \|SR\| = n, \|XZ\| = m and SR\|\|YZ. Find m in terms of n A. m = 2n B. m = 3n C. m = 4n D. m = 5n Show Content Detailed Solution \(\frac{n}{4} = \frac{m}{4 + 12}\) \(\frac{n}{4} = \frac{m}{16}\) 4m = 16n \(\frac{4m}{4} = \frac{16n}{4}\) m = 4n	C

65.	In the diagram, O is the centre of the circle and PQ is a diameter. Triangle RSO is an equilateral triangle of side 4cm. Find the area of the shaded region A. 43.36cm² B. 32.07² C. 18.21² D. 6.93² Show Content Detailed Solution Area of shaded portion = Area of semicircle Area of \(\bigtriangleup\) RSO Area of semicircle = \(\frac {\pi r^2}{2} = \frac{22\times 4 \times 4}{7 \times 3}\) = 25.14cm²; Area of \(\bigtriangleup\)RSO =\(\sqrt{s(s - 1)(s - b)(s - c)}\); where s = \(\frac{a + b + c}{2}\) s = \(\frac{4 + 4 + 4}{2}\) = 6cm = \(\sqrt{6(6 - 4)(6 - 4) (6 - 4)}\) = \(\sqrt{6(2) (2) (2)}\) = \(\sqrt{18}\) = 6.93cm² Area of shaded region = 25.14 - 6.93 &	C
66.	Find the product of 0.0409 and 0.0021 leaving your answer in the standard form A. 8.6 x 10^-6 B. 8.6 x 10⁵ C. 8.6 x 10^-4 D. 8.6 x 10⁵ Show Content Detailed Solution 0.0409 x 0.0021 = 409 x 10^-4 x 21 x 10^-4 = 409 x 21 x 10^-4-4 = 8589 x 10^-8 = 8.589 x 10³ x 10^-8 = 8.6 x 10^{3 - 8} = 8.6 x 10^-5	B
67.	Convert 42₅ to base three numeral A. 201₃ B. 210₃ C. 211₃ D. 343₃	C

Prev
1
2
3
4
5
6
7
Next