Year :
2007
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
51 - 60 of 67 Questions
| # | Question | Ans |
|---|---|---|
| 51. |
Find the smallest value of k such that 2\(^2\) x 3\(^3\) x 5 x k is a perfect square. A. 3 B. 5 C. 15 D. 30 Detailed Solution2\(^2\) x 3\(^3\) x 5\(^1\) x k;2\(^2\) x 3\(^2\) x 3 x 5 x k 2\(^2\) x 3\(^2\) x 15 x k smallest value for k 2\(^2\) x 3\(^2\) x 15 = 2\(^2\) x 3\(^2\) x 15\(^2\) k = 15 |
|
| 52. |
Expand the expression(3a - xy)(3a + xy) A. 9a2 - x2y2 B. 9a2 + x2y2 C. 9a2 - xy D. 9a2 + x2y Detailed Solution(3a - xy)(3a + xy); (3a)2 - (xy)2difference of two sqs; 9a2 - x2y2 |
|
| 53. |
Simplify \(\frac{4}{2x} - \frac{2x + x}{x}\) A. -1 B. -2x C. 2x D. \(\frac{2 - x}{2x}\) Detailed Solution\(\frac{4}{2x} - \frac{2 + x}{x} = \frac{4 - 2(2 + x)}{2x}\)= \(\frac{4 - 4 - 2x}{2x} = \frac{-2x}{2x}\) = 1 |
|
| 54. |
Two circles have radii 16cm and 23cm. What is the difference between their circumference? take \(\pi = \frac{22}{7}\) A. 422.92cm B. 149.92cm C. 44.00cm D. 43.96cm Detailed Solutionr = 16, R = 23; 2\(\pi R - 2 \pi r\)= 2\(\pi(R - r)\) = 2 x \(\frac{22}{7} (23 - 16)\) = 2 x \(\frac{22}{7} \times (7)\) = 44cm |
|
| 55. |
The volume of a cylinder is 1200cm3 and the area of its base is 150cm2. Find the height of the cylinder. A. 80.00cm B. 8.00cm C. 0.80cm D. 0.08cm Detailed SolutionVol. of cylinder = \(\pi r^2h\) = 1200cm2Area of base = \(\pi^2\) = 150cm2 h = \(\frac{\pi r^2}{\pi r^2} = \frac{1200}{150}\) = 8.00cm |
|
| 56. |
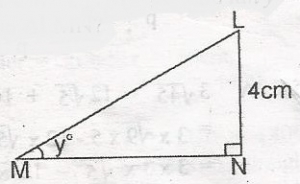 In the diagram |LN| = 4cm, LNM = 90o and tan y = \(\frac{2}{3}\). What is the area of the \(\bigtriangleup\)LMN? A. 24cm2 B. 12cm2 C. 10cm2 D. 6cm2 Detailed SolutionSince tan y = \(\frac{2}{3}\) and LN = 4tan y = \(\frac{2 \times 4}{3 \times 4} = \frac{8}{12} = \frac{4}{6}\) then tan y = \(\frac{opp}{adj}\) MN = 6cm Area of angle LMN = \(\frac{1}{2}\)bh = \(\frac{1}{2} \times 6 \times 4\) = 12cm3 |
|
| 57. |
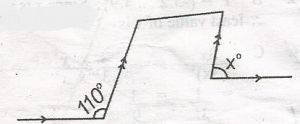
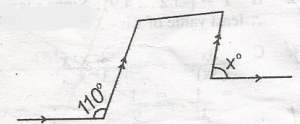 From the diagram, find the value of x in the diagram. A. 80o B. 70o C. 55o D. 35o Detailed Solution
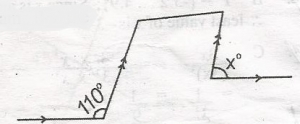 y = 180 - 110 = 70o x = y(corresponding angles) x = 70o |
|
| 58. |
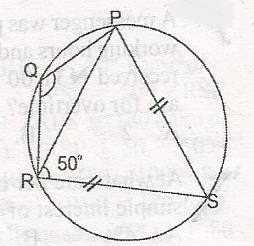
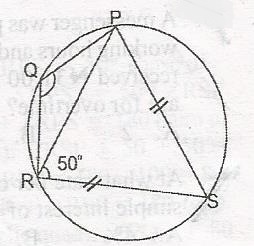 In the diagram, |SP| = |SR| and < PRS = 50o. Calculate < PQR A. 120o B. 110o C. 100o D. 80o Detailed Solution
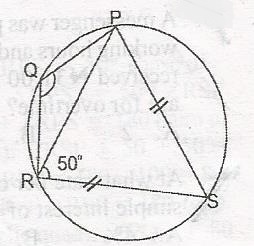 RPS = 50o; < RSP + < PRS + < RPS = 180(sum of < s in a triangle) < RPS + 50 + 50 = 180 < RSP = 180 - 100 = 80 then < PQR + < RSp = 180 (opp. < S of cyclic quad.) < PQR + 80 = 180o < PQR = 180 - 80 = 100 |
|
| 59. |
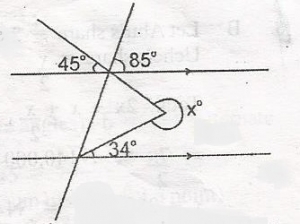 Find the value of x in the diagram A. 281o B. 269o C. 201o D. 179o Detailed Solutiona = 34o (alternate angles)b = 45o (alternate ngles) a + b = 34 + 45 = 79o x + 79 = 360(sum of angles at a point) x = 360 - 79 x = 281o |
|
| 60. |
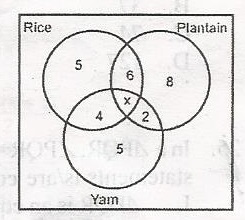 The venn diagram shows the choice of food of a number of visitors to a canteen. If there were 35 visitors in all, find the value of x A. 5 B. 4 C. 3 D. 2 Detailed Solution5 + 6 + 4 + 8 + 5 + 2 + x = 3530 + x = 35 x = 35 - 30 x = 5 |
| 51. |
Find the smallest value of k such that 2\(^2\) x 3\(^3\) x 5 x k is a perfect square. A. 3 B. 5 C. 15 D. 30 Detailed Solution2\(^2\) x 3\(^3\) x 5\(^1\) x k;2\(^2\) x 3\(^2\) x 3 x 5 x k 2\(^2\) x 3\(^2\) x 15 x k smallest value for k 2\(^2\) x 3\(^2\) x 15 = 2\(^2\) x 3\(^2\) x 15\(^2\) k = 15 |
|
| 52. |
Expand the expression(3a - xy)(3a + xy) A. 9a2 - x2y2 B. 9a2 + x2y2 C. 9a2 - xy D. 9a2 + x2y Detailed Solution(3a - xy)(3a + xy); (3a)2 - (xy)2difference of two sqs; 9a2 - x2y2 |
|
| 53. |
Simplify \(\frac{4}{2x} - \frac{2x + x}{x}\) A. -1 B. -2x C. 2x D. \(\frac{2 - x}{2x}\) Detailed Solution\(\frac{4}{2x} - \frac{2 + x}{x} = \frac{4 - 2(2 + x)}{2x}\)= \(\frac{4 - 4 - 2x}{2x} = \frac{-2x}{2x}\) = 1 |
|
| 54. |
Two circles have radii 16cm and 23cm. What is the difference between their circumference? take \(\pi = \frac{22}{7}\) A. 422.92cm B. 149.92cm C. 44.00cm D. 43.96cm Detailed Solutionr = 16, R = 23; 2\(\pi R - 2 \pi r\)= 2\(\pi(R - r)\) = 2 x \(\frac{22}{7} (23 - 16)\) = 2 x \(\frac{22}{7} \times (7)\) = 44cm |
|
| 55. |
The volume of a cylinder is 1200cm3 and the area of its base is 150cm2. Find the height of the cylinder. A. 80.00cm B. 8.00cm C. 0.80cm D. 0.08cm Detailed SolutionVol. of cylinder = \(\pi r^2h\) = 1200cm2Area of base = \(\pi^2\) = 150cm2 h = \(\frac{\pi r^2}{\pi r^2} = \frac{1200}{150}\) = 8.00cm |
| 56. |
 In the diagram |LN| = 4cm, LNM = 90o and tan y = \(\frac{2}{3}\). What is the area of the \(\bigtriangleup\)LMN? A. 24cm2 B. 12cm2 C. 10cm2 D. 6cm2 Detailed SolutionSince tan y = \(\frac{2}{3}\) and LN = 4tan y = \(\frac{2 \times 4}{3 \times 4} = \frac{8}{12} = \frac{4}{6}\) then tan y = \(\frac{opp}{adj}\) MN = 6cm Area of angle LMN = \(\frac{1}{2}\)bh = \(\frac{1}{2} \times 6 \times 4\) = 12cm3 |
|
| 57. |
 From the diagram, find the value of x in the diagram. A. 80o B. 70o C. 55o D. 35o Detailed Solution
 y = 180 - 110 = 70o x = y(corresponding angles) x = 70o |
|
| 58. |
 In the diagram, |SP| = |SR| and < PRS = 50o. Calculate < PQR A. 120o B. 110o C. 100o D. 80o Detailed Solution
 RPS = 50o; < RSP + < PRS + < RPS = 180(sum of < s in a triangle) < RPS + 50 + 50 = 180 < RSP = 180 - 100 = 80 then < PQR + < RSp = 180 (opp. < S of cyclic quad.) < PQR + 80 = 180o < PQR = 180 - 80 = 100 |
|
| 59. |
 Find the value of x in the diagram A. 281o B. 269o C. 201o D. 179o Detailed Solutiona = 34o (alternate angles)b = 45o (alternate ngles) a + b = 34 + 45 = 79o x + 79 = 360(sum of angles at a point) x = 360 - 79 x = 281o |
|
| 60. |
 The venn diagram shows the choice of food of a number of visitors to a canteen. If there were 35 visitors in all, find the value of x A. 5 B. 4 C. 3 D. 2 Detailed Solution5 + 6 + 4 + 8 + 5 + 2 + x = 3530 + x = 35 x = 35 - 30 x = 5 |