Year :
2005
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
1 - 10 of 47 Questions
| # | Question | Ans |
|---|---|---|
| 1. |
Find the value of m if 13m + 24m = 41m A. 8 B. 6 C. 5 D. 2 Detailed SolutionIf 13m + 24m = 41m1 * m1 + 3 0 + 2 * m1 + 4 * m0 = 4 * m1 + 1 * m0 1 * m + 3 * 1 + 2 * m + 4 * 1 = 4 * m + 1 * 1 m + 3 + 2m + 4 = 4m + 1 3m + 7 = 4m + 1 4m -3m = 7 - 1 m = 6 |
|
| 2. |
If 3214 is divided by 234 and leaves a remainder r, what is the value of r? A. zero B. 1 C. 2 D. 3 Detailed Solution\(\frac{321_4}{23_4}\\=\frac{(3\times4^{2})+(2\times4^{1})+(1\times4^{0})}{(2\times4^{0})+(3\times4^{0})}\\=\frac{3\times16+2\times4+1\times1}{2\times4+3\times1}\\=\frac{48+8+1}{8+3}\\=\frac{57}{11}=5\hspace{1mm}remainder\hspace{1mm}2\\∴r=2_{10} \\ Now\hspace{1mm}convert\hspace{1mm}2_{10} \hspace{1mm}to\hspace{1mm}base\hspace{1mm}4\\\frac{4}{2} = 2\\\frac{4}{0}=0\hspace{1mm}or\hspace{1mm}2\\∴r=2\) |
|
| 3. |
Simplify 31/2 - (21/3 * 11/4) + 3/5 A. 211/60 B. 21/60 C. 111/60 D. 11/60 Detailed Solution31/2 - (21/3 * 11/4) + 3/5= 7/2 - (7/3 * 5/4) + 3/5 = 7/2 - 35/12 + 3/5 = L.C.M = 60 = (210 - 175 + 36)/60 = 71/60 = 111< |
|
| 4. |
If the interest on N150.00 for 21/2 years is N4.50, find the interest on N250.00 for 6 months at the same rate A. N1.50 B. N7.50 C. N15.00 D. N18.00 Detailed Solution\(I = N4.50, P = N150,T=2\frac{1}{2}\hspace{1mm}years\\I=\frac{P\times T\times R}{100}\\4.50=\frac{150 \times 2\frac{1}{2} \times R}{100}\\\frac{4.50}{1}=\frac{150 \times 5 \times R}{100\times 2}\\4.50\times 4 = 15R\\R=\frac{4.50\times5}{15}\\R = \frac{6}{5}\\Again\hspace{1mm}I\hspace{1mm}=\frac{P\times T \times R}{100}\\=\frac{250\times 1 \times 6}{100\times 2\times 5}\\=\frac{3}{2}=N1.50\) |
|
| 5. |
Three boys shared some oranges. The first received 1/3 of the oranges and the second received 2/3 of the remaining. If the third boy received the remaining 12 oranges, how many oranges did they share A. 60 B. 54 C. 48 D. 42 Detailed SolutionLet x = the number of orangesThe 1st received 1/3 of x = 1/3x ∴Remainder = x - 1/3x = 2x/3 The 2nd received 2/3 of 2x/3 = 2/3 * 2x/3 = 4x/3 The 3rd received 12 oranges ∴1/3 |
|
| 6. |
Evaluate \(\frac{(81^{\frac{3}{4}}-27^{\frac{1}{3}})}{3 \times 2^3}\) A. 3 B. 1 C. 1/3 D. 1/8 Detailed Solution\(\frac{81^{\frac{3}{4}}-27^{\frac{1}{3}}}{3 \times 2^3} = \frac{(3^{3-\frac{3}{4}}-3^{3-\frac{3}{4}})}{3\times 2^3}\\=\frac{3^3 - 3}{3 \times 8}\\=\frac{27-3}{24}\\=\frac{24}{24}\\=1\) |
|
| 7. |
If Log102 = 0.3010 and Log103 = 0.4771, evaluate Log104.5 A. 0.9542 B. 0.6532 C. 0.4771 D. 0.3010 Detailed SolutionLog102 = 0.3010 and Log103 = 0.4771Log104.5 = Log1041/2 = Log109/2 = Log109 - Log102 = log1032 - Log102 = 2Log103 - Log102 = 2(0.4771) - 0.3010 = 0.9542 - 0.3010 = 0.6532 |
|
| 8. |
Simplify \(\frac{(√12-√3)}{(√12+√3)}\) A. zero B. 1/3 C. 3/5 D. 1 Detailed Solution\(\frac{(\sqrt{12}-\sqrt{3})}{(\sqrt{12}+\sqrt{3})}=\frac{\sqrt{4\times 3}-\sqrt{3}}{\sqrt{4\times 3}+\sqrt{3}}\\=\frac{2\sqrt{3}-\sqrt{3}}{2\sqrt{3}+\sqrt{3}}\\=\frac{\sqrt{3}}{3\sqrt{3}}\\=\frac{1}{3}\) |
|
| 9. |
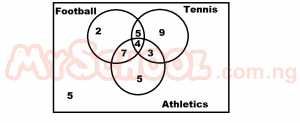 The venn diagram above shows a class of 40 students with the games they play. How many of the students play two games only? A. 19 B. 16 C. 15 D. 4 Detailed Solution
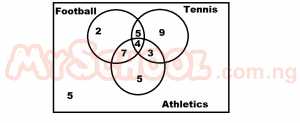 = 15 |
|
| 10. |
If m = 3, p = -3, q = 7 and r = 5/2, evaluate m(p+q+r) A. 19.50 B. 19.15 C. 18.95 D. 18.05 Detailed Solutionm = 3, p = -3, q = 7 and r = 5/2m(p+q+r) = 3(-3 + 7 + 5/2) = 3(4 + 5/2) = 3(4 + 21/2) = 3 * 61/2 = 3 * 13/2 = 39/2 = 19.50 |
| 1. |
Find the value of m if 13m + 24m = 41m A. 8 B. 6 C. 5 D. 2 Detailed SolutionIf 13m + 24m = 41m1 * m1 + 3 0 + 2 * m1 + 4 * m0 = 4 * m1 + 1 * m0 1 * m + 3 * 1 + 2 * m + 4 * 1 = 4 * m + 1 * 1 m + 3 + 2m + 4 = 4m + 1 3m + 7 = 4m + 1 4m -3m = 7 - 1 m = 6 |
|
| 2. |
If 3214 is divided by 234 and leaves a remainder r, what is the value of r? A. zero B. 1 C. 2 D. 3 Detailed Solution\(\frac{321_4}{23_4}\\=\frac{(3\times4^{2})+(2\times4^{1})+(1\times4^{0})}{(2\times4^{0})+(3\times4^{0})}\\=\frac{3\times16+2\times4+1\times1}{2\times4+3\times1}\\=\frac{48+8+1}{8+3}\\=\frac{57}{11}=5\hspace{1mm}remainder\hspace{1mm}2\\∴r=2_{10} \\ Now\hspace{1mm}convert\hspace{1mm}2_{10} \hspace{1mm}to\hspace{1mm}base\hspace{1mm}4\\\frac{4}{2} = 2\\\frac{4}{0}=0\hspace{1mm}or\hspace{1mm}2\\∴r=2\) |
|
| 3. |
Simplify 31/2 - (21/3 * 11/4) + 3/5 A. 211/60 B. 21/60 C. 111/60 D. 11/60 Detailed Solution31/2 - (21/3 * 11/4) + 3/5= 7/2 - (7/3 * 5/4) + 3/5 = 7/2 - 35/12 + 3/5 = L.C.M = 60 = (210 - 175 + 36)/60 = 71/60 = 111< |
|
| 4. |
If the interest on N150.00 for 21/2 years is N4.50, find the interest on N250.00 for 6 months at the same rate A. N1.50 B. N7.50 C. N15.00 D. N18.00 Detailed Solution\(I = N4.50, P = N150,T=2\frac{1}{2}\hspace{1mm}years\\I=\frac{P\times T\times R}{100}\\4.50=\frac{150 \times 2\frac{1}{2} \times R}{100}\\\frac{4.50}{1}=\frac{150 \times 5 \times R}{100\times 2}\\4.50\times 4 = 15R\\R=\frac{4.50\times5}{15}\\R = \frac{6}{5}\\Again\hspace{1mm}I\hspace{1mm}=\frac{P\times T \times R}{100}\\=\frac{250\times 1 \times 6}{100\times 2\times 5}\\=\frac{3}{2}=N1.50\) |
|
| 5. |
Three boys shared some oranges. The first received 1/3 of the oranges and the second received 2/3 of the remaining. If the third boy received the remaining 12 oranges, how many oranges did they share A. 60 B. 54 C. 48 D. 42 Detailed SolutionLet x = the number of orangesThe 1st received 1/3 of x = 1/3x ∴Remainder = x - 1/3x = 2x/3 The 2nd received 2/3 of 2x/3 = 2/3 * 2x/3 = 4x/3 The 3rd received 12 oranges ∴1/3 |
| 6. |
Evaluate \(\frac{(81^{\frac{3}{4}}-27^{\frac{1}{3}})}{3 \times 2^3}\) A. 3 B. 1 C. 1/3 D. 1/8 Detailed Solution\(\frac{81^{\frac{3}{4}}-27^{\frac{1}{3}}}{3 \times 2^3} = \frac{(3^{3-\frac{3}{4}}-3^{3-\frac{3}{4}})}{3\times 2^3}\\=\frac{3^3 - 3}{3 \times 8}\\=\frac{27-3}{24}\\=\frac{24}{24}\\=1\) |
|
| 7. |
If Log102 = 0.3010 and Log103 = 0.4771, evaluate Log104.5 A. 0.9542 B. 0.6532 C. 0.4771 D. 0.3010 Detailed SolutionLog102 = 0.3010 and Log103 = 0.4771Log104.5 = Log1041/2 = Log109/2 = Log109 - Log102 = log1032 - Log102 = 2Log103 - Log102 = 2(0.4771) - 0.3010 = 0.9542 - 0.3010 = 0.6532 |
|
| 8. |
Simplify \(\frac{(√12-√3)}{(√12+√3)}\) A. zero B. 1/3 C. 3/5 D. 1 Detailed Solution\(\frac{(\sqrt{12}-\sqrt{3})}{(\sqrt{12}+\sqrt{3})}=\frac{\sqrt{4\times 3}-\sqrt{3}}{\sqrt{4\times 3}+\sqrt{3}}\\=\frac{2\sqrt{3}-\sqrt{3}}{2\sqrt{3}+\sqrt{3}}\\=\frac{\sqrt{3}}{3\sqrt{3}}\\=\frac{1}{3}\) |
|
| 9. |
 The venn diagram above shows a class of 40 students with the games they play. How many of the students play two games only? A. 19 B. 16 C. 15 D. 4 Detailed Solution
 = 15 |
|
| 10. |
If m = 3, p = -3, q = 7 and r = 5/2, evaluate m(p+q+r) A. 19.50 B. 19.15 C. 18.95 D. 18.05 Detailed Solutionm = 3, p = -3, q = 7 and r = 5/2m(p+q+r) = 3(-3 + 7 + 5/2) = 3(4 + 5/2) = 3(4 + 21/2) = 3 * 61/2 = 3 * 13/2 = 39/2 = 19.50 |