Year :
2005
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 47 of 47 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
How many possible ways are there of seating seven people P,Q,R,S,T,U and V at a circular table A. 360 B. 720 C. 2520 D. 5040 Detailed Solution(n - 1)! = (7 - 1)!= 6! = 6*5*4*3*2*1 = 720 ways |
|
| 42. |
A box contains 5 blue balls, 3 red balls and 2 white balls. Two balls are selected from the box with replacement. Find the probability of obtaining two blue or two red balls A. 17/50 B. 3/25 C. 1/50 D. 3/250 Detailed SolutionBlue balls = 5Red balls = 3 White balls = 2 Total = 10 P(Two blue) = 5/10 * 5/10 = 25/100 P(Two Red) = 3/10 * 3/10 = 9/100 ∴P(Two blue or two red balls) = 25/100 + 9/100 = 34/100 = 17/50 |
|
| 43. |
What is the probability that an integer x,(1 \(\leq\) x \(\leq\) 20) chosen at random is divisible by both 2 and 3? A. 1/20 B. 1/3 C. 3/20 D. 7/10 Detailed SolutionU = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}A = {x/x is divisible by 2} A = {2,4,6,8,10,12,14,16,18,20} B = {x/x is divisible by 3} A ∩ B = {6, 12, 18} P(Number divisible by both 2 and 3) = 3/20 |
|
| 44. |
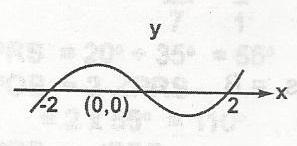 The diagram above is the graph of the function f(x). Determine the range of values of x for which f(x) \(\geq\) 0. A. x \(\geq\) 2 B. 0 \(\geq\) x \(\geq\) 2 C. -2 \(\geq\) x \(\geq\) 0, x \(\leq\) 2 D. x \(\geq\) -2, 0 \(\geq\) x \(\geq\) 2 |
C |
| 45. |
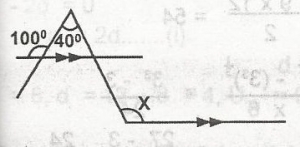 In the diagram above, calculate the value of x. A. 60o B. 100o C. 120o D. 140o |
C |
| 46. |
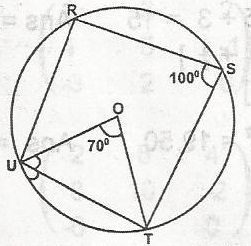 In the diagram above, O is the centre of the circle, If < UOT = 70o and < RST = 100o. Calculate < RUO A. 20o B. 25o C. 50o D. 80o Detailed Solution< OUT = < OTU< OUT = \(\frac{180^o - 70^o}{2} = \frac{110^o}{2} = 55^o\) < RUT = 180o - 100o = 80o < RUO = < RUT - < OUT = 80o - 55o = 25o |
|
| 47. |
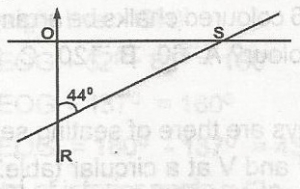 From the diagram given, find the bearing of R from S A. 226o B. 224o C. 136o D. 134o Detailed SolutionThe bearing of R from S = 180 + 44 = 224º, because-Following the clockwise movement at 90º: -NORTH -EAST, EAST-SOUTH, SOUTH - WEST & WEST - NORTH - It is observed that R is situated between SOUTH - WEST poles on S |
| 41. |
How many possible ways are there of seating seven people P,Q,R,S,T,U and V at a circular table A. 360 B. 720 C. 2520 D. 5040 Detailed Solution(n - 1)! = (7 - 1)!= 6! = 6*5*4*3*2*1 = 720 ways |
|
| 42. |
A box contains 5 blue balls, 3 red balls and 2 white balls. Two balls are selected from the box with replacement. Find the probability of obtaining two blue or two red balls A. 17/50 B. 3/25 C. 1/50 D. 3/250 Detailed SolutionBlue balls = 5Red balls = 3 White balls = 2 Total = 10 P(Two blue) = 5/10 * 5/10 = 25/100 P(Two Red) = 3/10 * 3/10 = 9/100 ∴P(Two blue or two red balls) = 25/100 + 9/100 = 34/100 = 17/50 |
|
| 43. |
What is the probability that an integer x,(1 \(\leq\) x \(\leq\) 20) chosen at random is divisible by both 2 and 3? A. 1/20 B. 1/3 C. 3/20 D. 7/10 Detailed SolutionU = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}A = {x/x is divisible by 2} A = {2,4,6,8,10,12,14,16,18,20} B = {x/x is divisible by 3} A ∩ B = {6, 12, 18} P(Number divisible by both 2 and 3) = 3/20 |
|
| 44. |
 The diagram above is the graph of the function f(x). Determine the range of values of x for which f(x) \(\geq\) 0. A. x \(\geq\) 2 B. 0 \(\geq\) x \(\geq\) 2 C. -2 \(\geq\) x \(\geq\) 0, x \(\leq\) 2 D. x \(\geq\) -2, 0 \(\geq\) x \(\geq\) 2 |
C |
| 45. |
 In the diagram above, calculate the value of x. A. 60o B. 100o C. 120o D. 140o |
C |
| 46. |
 In the diagram above, O is the centre of the circle, If < UOT = 70o and < RST = 100o. Calculate < RUO A. 20o B. 25o C. 50o D. 80o Detailed Solution< OUT = < OTU< OUT = \(\frac{180^o - 70^o}{2} = \frac{110^o}{2} = 55^o\) < RUT = 180o - 100o = 80o < RUO = < RUT - < OUT = 80o - 55o = 25o |
|
| 47. |
 From the diagram given, find the bearing of R from S A. 226o B. 224o C. 136o D. 134o Detailed SolutionThe bearing of R from S = 180 + 44 = 224º, because-Following the clockwise movement at 90º: -NORTH -EAST, EAST-SOUTH, SOUTH - WEST & WEST - NORTH - It is observed that R is situated between SOUTH - WEST poles on S |