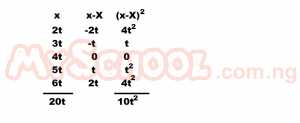Year :
2005
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
31 - 40 of 47 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
The radius r of a circular disc is increasing at the rate of 0.5cm/sec. At what rate is the area of the disc increasing when its radius is 6cm? A. 36 π cm2/sec B. 18 π cm2/sec C. 6 π cm2/sec D. 3 π cm2/sec Detailed SolutionIncrease in radius dr/dt = 0.5Area of the circular disc = πr2 Increase in area: dA/dr = 2πr Rate of increase in area: dA/dt = dA/dr * dr/dt when r = 6cm = 2πr * 0.5 = 2 * π * 6 * 0.5 2 * π * 6 * 1/2 = 6 π cm2/sec |
|
| 32. |
The maximum value of the function A. 9/4 B. 7/4 C. 3/2 D. 1/2 Detailed Solutionf(x) = 2 + x - x2dy/dx = 1-2x As dy/dx = 0 1-2x = 0 2x = 1 x = 1/2 At x = 1/2 f(x) = 2 + x - x2 = 2 + 1/2 -(1/2)2 = 2 + 1/2 - 1/4 = (8+2-1) / 4 = 9/4 |
|
| 33. |
Find the area of the figure bounded by the given pair of curves y = x2 - x + 3 and y = 3 A. 17/6 units (sq) B. 7/6 units (sq) C. 5/6 units (sq) D. 1/6 units (sq) Detailed SolutionArea bounded byy = x2 - x + 3 and y = 3 x2 - x + 3 = 3 x2 - x = 0 x(x -1) = 0 x= 0 and x = 1 \(\int^{1}_{0}\)(x2 - x + 3)dx = [1/3x3 - 1/2x2 + 3x]\(^1 _0\) (1/3(1)3 - 1/2(1)2 + 3(1) - (1/3(0)3 - 1/2 |
|
| 34. |
Evaluate \(\int_0^{\frac{\pi}{2}}sin2xdx\) A. 1 B. zero C. -1/2 D. -1 Detailed Solution\(\int_0^{\frac{\pi}{2}}\)sin 2x dx = [-1/2cos 2x + C]\(_0^{\frac{\pi}{2}}\)=[-1/2 cos 2 * π/2 + C] - [-1/2 cos 2 * 0] = [-1/2 cos π] - [-1/2 cos 0] = [-1/2x - 1] - [-1/2 * 1] = 1/2 -(-1/2) = 1/2 + 1/2 = 1 |
|
| 35. |
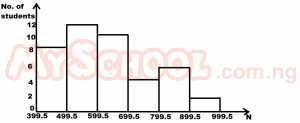 The histogram above shows the distribution of monthly incomes of the workers in a company. How many workers earn more than N700.00? A. 16 B. 12 C. 8 D. 6 |
B |
| 36. |
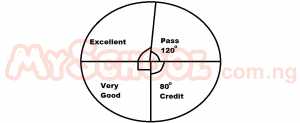 The grades of 36 students in a test are shown in the pie chart above. How many students had excellent? A. 7 B. 8 C. 9 D. 12 Detailed SolutionAngle of Excellent= 360 - (120+80+90) = 360 - 290 = 70o If 360o represents 36 students 1o will represent 36/360 50o will represent 36/360 * 70/1 = 7 |
|
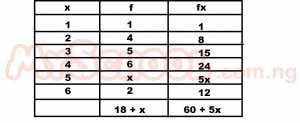
| 37. |
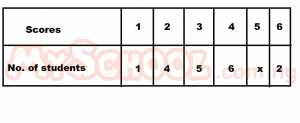 The table above shows that the scores of a group of students in a test. If the average score is 3.5, find the value of x A. 1 B. 2 C. 3 D. 4 Detailed Solution
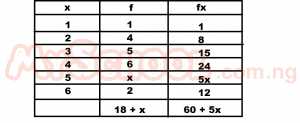 7(18+x) = 2(60+5x) 126 + 7x = 120 + 10x 10x - 7x = 126 - 120 3x = 6 x = 2 |
|
| 38. |
The model height and range of heights 1.35, 1.25, 1.35, 1.40, 1.35, 1.50, 1.35, 1.50, and 1.20 are m and r respectively. Find m+2r. A. 1.35 B. 1.65 C. 1.95 D. 3.00 Detailed Solution1.35, 1.25, 1.35, 1.40, 1.35, 1.50, 1.35, 1.50, and 1.20Modal height = 1.35 Range (r) = 1.50 - 1.20 = 0.30 ∴m + 2r = 1.35 + 2(0.30) = 1.35 + 0.60 = 1.95 |
|
| 39. |
Find the value of t if the standard deviation of 2t, 3t, 4t, 5t, and 6t is √2 A. 1 B. 2 C. 3 D. 4 Detailed Solution
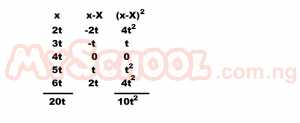 |
|
| 40. |
In how many ways can 6coloured chalks be arranged if 2 are same colour? A. 60 B. 120 C. 240 D. 360 Detailed Solution\(\frac{6!}{2!}=ways=\frac{6\times5\times4\times3\times2!}{2!}\\=6\times5\times4\times3\\=360\hspace{1mm}ways\) |
| 31. |
The radius r of a circular disc is increasing at the rate of 0.5cm/sec. At what rate is the area of the disc increasing when its radius is 6cm? A. 36 π cm2/sec B. 18 π cm2/sec C. 6 π cm2/sec D. 3 π cm2/sec Detailed SolutionIncrease in radius dr/dt = 0.5Area of the circular disc = πr2 Increase in area: dA/dr = 2πr Rate of increase in area: dA/dt = dA/dr * dr/dt when r = 6cm = 2πr * 0.5 = 2 * π * 6 * 0.5 2 * π * 6 * 1/2 = 6 π cm2/sec |
|
| 32. |
The maximum value of the function A. 9/4 B. 7/4 C. 3/2 D. 1/2 Detailed Solutionf(x) = 2 + x - x2dy/dx = 1-2x As dy/dx = 0 1-2x = 0 2x = 1 x = 1/2 At x = 1/2 f(x) = 2 + x - x2 = 2 + 1/2 -(1/2)2 = 2 + 1/2 - 1/4 = (8+2-1) / 4 = 9/4 |
|
| 33. |
Find the area of the figure bounded by the given pair of curves y = x2 - x + 3 and y = 3 A. 17/6 units (sq) B. 7/6 units (sq) C. 5/6 units (sq) D. 1/6 units (sq) Detailed SolutionArea bounded byy = x2 - x + 3 and y = 3 x2 - x + 3 = 3 x2 - x = 0 x(x -1) = 0 x= 0 and x = 1 \(\int^{1}_{0}\)(x2 - x + 3)dx = [1/3x3 - 1/2x2 + 3x]\(^1 _0\) (1/3(1)3 - 1/2(1)2 + 3(1) - (1/3(0)3 - 1/2 |
|
| 34. |
Evaluate \(\int_0^{\frac{\pi}{2}}sin2xdx\) A. 1 B. zero C. -1/2 D. -1 Detailed Solution\(\int_0^{\frac{\pi}{2}}\)sin 2x dx = [-1/2cos 2x + C]\(_0^{\frac{\pi}{2}}\)=[-1/2 cos 2 * π/2 + C] - [-1/2 cos 2 * 0] = [-1/2 cos π] - [-1/2 cos 0] = [-1/2x - 1] - [-1/2 * 1] = 1/2 -(-1/2) = 1/2 + 1/2 = 1 |
|
| 35. |
 The histogram above shows the distribution of monthly incomes of the workers in a company. How many workers earn more than N700.00? A. 16 B. 12 C. 8 D. 6 |
B |
| 36. |
 The grades of 36 students in a test are shown in the pie chart above. How many students had excellent? A. 7 B. 8 C. 9 D. 12 Detailed SolutionAngle of Excellent= 360 - (120+80+90) = 360 - 290 = 70o If 360o represents 36 students 1o will represent 36/360 50o will represent 36/360 * 70/1 = 7 |
|
| 37. |
 The table above shows that the scores of a group of students in a test. If the average score is 3.5, find the value of x A. 1 B. 2 C. 3 D. 4 Detailed Solution
 7(18+x) = 2(60+5x) 126 + 7x = 120 + 10x 10x - 7x = 126 - 120 3x = 6 x = 2 |
|
| 38. |
The model height and range of heights 1.35, 1.25, 1.35, 1.40, 1.35, 1.50, 1.35, 1.50, and 1.20 are m and r respectively. Find m+2r. A. 1.35 B. 1.65 C. 1.95 D. 3.00 Detailed Solution1.35, 1.25, 1.35, 1.40, 1.35, 1.50, 1.35, 1.50, and 1.20Modal height = 1.35 Range (r) = 1.50 - 1.20 = 0.30 ∴m + 2r = 1.35 + 2(0.30) = 1.35 + 0.60 = 1.95 |
|
| 39. |
Find the value of t if the standard deviation of 2t, 3t, 4t, 5t, and 6t is √2 A. 1 B. 2 C. 3 D. 4 Detailed Solution
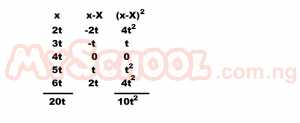 |
|
| 40. |
In how many ways can 6coloured chalks be arranged if 2 are same colour? A. 60 B. 120 C. 240 D. 360 Detailed Solution\(\frac{6!}{2!}=ways=\frac{6\times5\times4\times3\times2!}{2!}\\=6\times5\times4\times3\\=360\hspace{1mm}ways\) |