Year :
1994
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
21 - 30 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 21. |
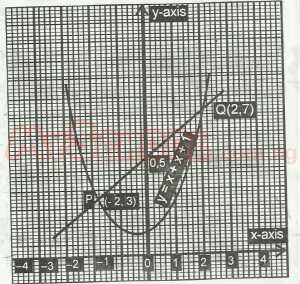 Which of the following equations can be solved by the points of intersection P and Q of the curve and the line PQ? A. x2 - 2 = 0 B. x2 - 4 = 0 C. x2 + 6 = 0 D. X2 - X – 2 = 0 E. x2 - x + 4 = 0 Detailed SolutionThe points of intersection of the curve and the line are at x = -2 and x = 2.\(\therefore\) (x + 2) = 0; (x - 2) = 0. (x + 2)(x - 2) = 0 \(x^2 - 4 = 0\) |
|
| 22. |
Which of the following is not a factors of 2p\(^2\) - 2? A. 2 B. p - 1 C. p + 1 D. 2p - 2 E. 2p + 1 Detailed Solution2p\(^2\) - 22(p\(^2\) - 1) = 2(p + 1)(p - 1) |
|
| 23. |
Find the quadratic equation whose roots are 3 and \(\frac{2}{3}\). A. x2 - 11 / 3x + 6 = 0 B. x2 - 11x + 6 = O C. 3x2 - 11x + 2 = O D. 3X2 - 11x – 2 = 0 E. 3x2 - 11x + 6 = 0 Detailed Solutionx = 3; x = \(\frac{2}{3}\).(x - 3)(x - \(\frac{2}{3}\)) = 0 \(x^2 - \frac{2x}{3} - 3x + 2 = 0\) \(x^2 - \frac{11x}{3} + 2 = 0\) \(3x^2 - 11x + 6 = 0\) |
|
| 24. |
Which of the following is a root of the equation x\(^2\) +6x = 0? A. 0 B. 1 C. 2 D. 3 E. It does not have any root. Detailed Solution\(x^2 + 6x = 0\)\(x(x + 6) = 0\) \(x = 0\) or \(x = -6\) |
|
| 25. |
Factorise: 6x\(^2\) + 7xy - 5y\(^2\) A. (6x + 5y)(x - y) B. (2x + 5y)(3x - y) C. (3x + y)(2x - 5y) D. (3x + 5y)(2x - y) E. (2x + y)(3x - 5y) Detailed Solution\(6x^2 + 7xy - 5y^2\)= \(6x^2 + 10xy - 3xy - 5y^2\) = \(2x(3x + 5y) - y(3x + 5y)\) = \((2x - y)(3x + 5y)\) |
|
| 26. |
Solve the equation log8x - 4log8x = 2 A. 1/4 B. 1/2 C. 1 D. 2 E. 4 Detailed Solutionlog8x - 4log8x = 2; log8x - log8x4 = 2log8x/x4 = 2 x/x4 = 82 = 1/x3 = 64 x3 = (1/4)3; x = 1/4 |
|
| 27. |
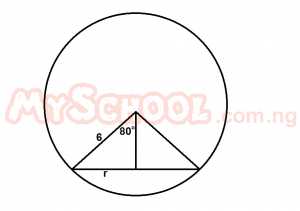
The angle subtended at the centre by a chord of a circle radius 6cm is 120°. Find the length of the chord. A. 3cm B. 6cm C. \(4\sqrt{2}\) cm D. \(3\sqrt{3}\) cm E. \(6\sqrt{3}\) cm Detailed Solution
\(r = 6 \sin 60\) = \(6 \times \frac{\sqrt{3}}{2}\) = \(3\sqrt{3}\) Chord = 2r = \( 2 \times 3\sqrt{3}\) = \(6\sqrt{3}\) |
|
| 28. |
A cuboid of base 12.5cm by 20cm holds exactly 1 litre of water. What is the height of the cuboid? (1 litre =1000cm3) A. 2cm B. 4cm C. 5cm D. 8cm E. 10cm Detailed SolutionVolume of cuboid = length x breadth x height12.5 x 20 x h = 1000 250h = 1000 h = 4 cm |
|
| 29. |
Two ships on the equator are on longitudes 45oW and 45oE respectively. How far are they apart along the equator, correct to 2 significant figures? (Take the radius of earth = 6400km and π = 22/7) A. 15,000km B. 10,000km C. 6,400km D. 5,000km E. 3,200km Detailed SolutionD = θ/360 x 2πR45 + 45360o x 447 x 6400= 10057 ≅ 10000km |
|
| 30. |
Calculate, correct to 2 significant figures, the length of the arc of a circle of radius 3.5cm which subtends an angle of 75° at the centre of the circle. [Take π = 22/7]. A. 2.3cm B. 4.6cm C. 8cm D. 16cm E. 110cm Detailed SolutionLength of arc = \(\frac{\theta}{360} \times 2\pi r\)= \(\frac{75}{360} \times 2 \times \frac{22}{7} \times 3.5\) = \(4.583 cm\) \(\approxeq\) 4.6 cm (to 2 sig. figs) |
| 21. |
 Which of the following equations can be solved by the points of intersection P and Q of the curve and the line PQ? A. x2 - 2 = 0 B. x2 - 4 = 0 C. x2 + 6 = 0 D. X2 - X – 2 = 0 E. x2 - x + 4 = 0 Detailed SolutionThe points of intersection of the curve and the line are at x = -2 and x = 2.\(\therefore\) (x + 2) = 0; (x - 2) = 0. (x + 2)(x - 2) = 0 \(x^2 - 4 = 0\) |
|
| 22. |
Which of the following is not a factors of 2p\(^2\) - 2? A. 2 B. p - 1 C. p + 1 D. 2p - 2 E. 2p + 1 Detailed Solution2p\(^2\) - 22(p\(^2\) - 1) = 2(p + 1)(p - 1) |
|
| 23. |
Find the quadratic equation whose roots are 3 and \(\frac{2}{3}\). A. x2 - 11 / 3x + 6 = 0 B. x2 - 11x + 6 = O C. 3x2 - 11x + 2 = O D. 3X2 - 11x – 2 = 0 E. 3x2 - 11x + 6 = 0 Detailed Solutionx = 3; x = \(\frac{2}{3}\).(x - 3)(x - \(\frac{2}{3}\)) = 0 \(x^2 - \frac{2x}{3} - 3x + 2 = 0\) \(x^2 - \frac{11x}{3} + 2 = 0\) \(3x^2 - 11x + 6 = 0\) |
|
| 24. |
Which of the following is a root of the equation x\(^2\) +6x = 0? A. 0 B. 1 C. 2 D. 3 E. It does not have any root. Detailed Solution\(x^2 + 6x = 0\)\(x(x + 6) = 0\) \(x = 0\) or \(x = -6\) |
|
| 25. |
Factorise: 6x\(^2\) + 7xy - 5y\(^2\) A. (6x + 5y)(x - y) B. (2x + 5y)(3x - y) C. (3x + y)(2x - 5y) D. (3x + 5y)(2x - y) E. (2x + y)(3x - 5y) Detailed Solution\(6x^2 + 7xy - 5y^2\)= \(6x^2 + 10xy - 3xy - 5y^2\) = \(2x(3x + 5y) - y(3x + 5y)\) = \((2x - y)(3x + 5y)\) |
| 26. |
Solve the equation log8x - 4log8x = 2 A. 1/4 B. 1/2 C. 1 D. 2 E. 4 Detailed Solutionlog8x - 4log8x = 2; log8x - log8x4 = 2log8x/x4 = 2 x/x4 = 82 = 1/x3 = 64 x3 = (1/4)3; x = 1/4 |
|
| 27. |
The angle subtended at the centre by a chord of a circle radius 6cm is 120°. Find the length of the chord. A. 3cm B. 6cm C. \(4\sqrt{2}\) cm D. \(3\sqrt{3}\) cm E. \(6\sqrt{3}\) cm Detailed Solution
\(r = 6 \sin 60\) = \(6 \times \frac{\sqrt{3}}{2}\) = \(3\sqrt{3}\) Chord = 2r = \( 2 \times 3\sqrt{3}\) = \(6\sqrt{3}\) |
|
| 28. |
A cuboid of base 12.5cm by 20cm holds exactly 1 litre of water. What is the height of the cuboid? (1 litre =1000cm3) A. 2cm B. 4cm C. 5cm D. 8cm E. 10cm Detailed SolutionVolume of cuboid = length x breadth x height12.5 x 20 x h = 1000 250h = 1000 h = 4 cm |
|
| 29. |
Two ships on the equator are on longitudes 45oW and 45oE respectively. How far are they apart along the equator, correct to 2 significant figures? (Take the radius of earth = 6400km and π = 22/7) A. 15,000km B. 10,000km C. 6,400km D. 5,000km E. 3,200km Detailed SolutionD = θ/360 x 2πR45 + 45360o x 447 x 6400= 10057 ≅ 10000km |
|
| 30. |
Calculate, correct to 2 significant figures, the length of the arc of a circle of radius 3.5cm which subtends an angle of 75° at the centre of the circle. [Take π = 22/7]. A. 2.3cm B. 4.6cm C. 8cm D. 16cm E. 110cm Detailed SolutionLength of arc = \(\frac{\theta}{360} \times 2\pi r\)= \(\frac{75}{360} \times 2 \times \frac{22}{7} \times 3.5\) = \(4.583 cm\) \(\approxeq\) 4.6 cm (to 2 sig. figs) |