Year :
1994
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
11 - 20 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 11. |
A string is 4.8m. A boy measured it to be 4.95m. Find the percentage error. A. \( \frac{5}{16} \)% B. \(1\frac{5}{16} \)% C. \( 3\frac{1}{33} \)% D. \( 3\frac{1}{8} \)% E. 25% Detailed Solution4.95m - 4.8m = 0.15m\(\frac{0.15}{4.8} \times 100%\) = \(\frac{25}{8}\) = \(3\frac{1}{8} %) |
|
| 12. |
The sum of the 1st and 2nd terms of an A.P. is 4 and the 10th term is 19. Find the sum of the 5th and 6th terms. A. 11 B. 20 C. 21 D. 22 E. 24 Detailed Solution\(T_{n} = a + (n - 1) d\) (terms of an A.P)\(T_{1} = a\) \(T_{2} = a + d\) \(T_{10} = a + 9d\) \(a + a + d = 2a + d = 4 ... (i)\) \(a + 9d = 19 ... (ii)\) (ii) x 2: \(2a + 18d = 38 ... (iii)\) (iii) - (i) : \(17d = 34 \implies d = 2\) \(2a + 2 = 4 \implies 2a = 2\) \(a = 1\) \(T_{5} + T_{6}\) = \((a + 4d) + (a + 5d)\) = \(2a + 9d\) = \(2(1) + 9(2)\) = 20 |
|
| 13. |
E = (integers \(\leq\) 20), P = (multiples of 3), Q = (multiples of 4), what are the elements of P'∩Q? A. (12) B. (4, 8, 16, 20) C. (3, 6, 9, 15, 18) D. (1,2,5,7,10,11,13,17,19) E. (3, 4, 6, 8, 9, 12, 15, 16, 18, 20) Detailed SolutionE = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}P = {3, 6, 9, 12, 15, 18} Q = {4, 8, 12, 16, 20} P' = {1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20} P' \(\cap\) Q = {4, 8, 16, 20} |
|
| 14. |
Given that 2p - m = 6 and 2p + 4m = 1, find the value of (4p + 3m). A. 1 B. 3 C. 5 D. 7 E. 9 Detailed Solution2p - m = 6 ... (i)2p + 4m = 1 ... (ii) From (i), m = 2p - 6. 2p + 4(2p - 6) = 1 2p + 8p - 24 = 1 10p = 1 + 24 = 25 p = 2.5 m = 2(2.5) - 6 = 5 - 6 = -1 \(\therefore\) 4p + 3m = 4(2.5) + 3(-1) = 10 - 3 = 7 |
|
| 15. |
Which of the following is a point on the curve y = x\(^2\) - 4x + 7? A. (0,6) B. (1,4) C. (2,0) D. (7,0) E. (3,2) |
B |
| 16. |
If 8x- 4 = 6x- 10, find the value of 5x, A. -35 B. -15 C. -3 D. 3 E. 7 Detailed Solution8x - 4 = 6x - 108x - 6x = -10 + 4 2x = -6 x = -3 \(\therefore\) 5x = 5(-3) = -15 |
|
| 17. |
For what value of x is the expression \(\frac{x^2 + 15x + 50}{x - 5}\) not defined ? A. -10 B. -5 C. o D. 5 E. 10 Detailed Solution\(\frac{x^2 + 15x + 50}{x - 5}\)It is undefined when x - 5 = 0. That is at x = 5. |
|
| 18. |
If x is positive, for what range of values of x is 4 + 3x < 10? A. 0 < x < 2 B. x < 2 C. 1 < x < 2 D. 0 < x < 4 3 4 E. 0 > x > 2 Detailed Solution4 + 3x < 103x < 10 - 4 3x < 6 x < 2 |
|
| 19. |
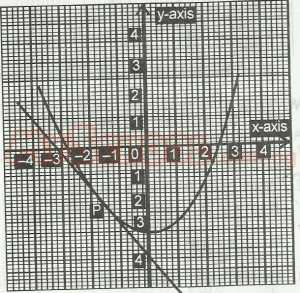 In the graph above, the gradient of the curve at the point P is A. -11 3 B. -3 4 C. 3/7 D. 3/4 E. 11 3 Detailed Solution-1-(-3)/-2-(-0.5) = 2/-1.5 = 20/-15 = -113 |
|
| 20. |
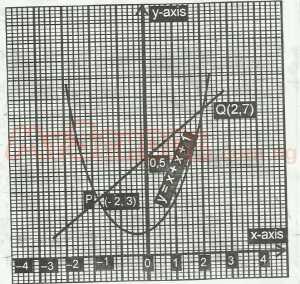 What is the equation of the line PQ? A. y = x - 5 B. y = x + 3 C. y = x + 5 D. y = 2x + 3 E. y = 2x - 3 Detailed SolutionThe points P(-2, 3) and Q(2, 7) are on the line.Gradient of the line = \(\frac{7 - 3}{2 - (-2)}\) = \(\frac{4}{4}\) = 1 y = x + b To find the intercept, we have 7 = 2 + b or 3 = -2 + b. Solving for b, we get b = 5. \(\therefore\) The line is y = x + 5. |
| 11. |
A string is 4.8m. A boy measured it to be 4.95m. Find the percentage error. A. \( \frac{5}{16} \)% B. \(1\frac{5}{16} \)% C. \( 3\frac{1}{33} \)% D. \( 3\frac{1}{8} \)% E. 25% Detailed Solution4.95m - 4.8m = 0.15m\(\frac{0.15}{4.8} \times 100%\) = \(\frac{25}{8}\) = \(3\frac{1}{8} %) |
|
| 12. |
The sum of the 1st and 2nd terms of an A.P. is 4 and the 10th term is 19. Find the sum of the 5th and 6th terms. A. 11 B. 20 C. 21 D. 22 E. 24 Detailed Solution\(T_{n} = a + (n - 1) d\) (terms of an A.P)\(T_{1} = a\) \(T_{2} = a + d\) \(T_{10} = a + 9d\) \(a + a + d = 2a + d = 4 ... (i)\) \(a + 9d = 19 ... (ii)\) (ii) x 2: \(2a + 18d = 38 ... (iii)\) (iii) - (i) : \(17d = 34 \implies d = 2\) \(2a + 2 = 4 \implies 2a = 2\) \(a = 1\) \(T_{5} + T_{6}\) = \((a + 4d) + (a + 5d)\) = \(2a + 9d\) = \(2(1) + 9(2)\) = 20 |
|
| 13. |
E = (integers \(\leq\) 20), P = (multiples of 3), Q = (multiples of 4), what are the elements of P'∩Q? A. (12) B. (4, 8, 16, 20) C. (3, 6, 9, 15, 18) D. (1,2,5,7,10,11,13,17,19) E. (3, 4, 6, 8, 9, 12, 15, 16, 18, 20) Detailed SolutionE = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}P = {3, 6, 9, 12, 15, 18} Q = {4, 8, 12, 16, 20} P' = {1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20} P' \(\cap\) Q = {4, 8, 16, 20} |
|
| 14. |
Given that 2p - m = 6 and 2p + 4m = 1, find the value of (4p + 3m). A. 1 B. 3 C. 5 D. 7 E. 9 Detailed Solution2p - m = 6 ... (i)2p + 4m = 1 ... (ii) From (i), m = 2p - 6. 2p + 4(2p - 6) = 1 2p + 8p - 24 = 1 10p = 1 + 24 = 25 p = 2.5 m = 2(2.5) - 6 = 5 - 6 = -1 \(\therefore\) 4p + 3m = 4(2.5) + 3(-1) = 10 - 3 = 7 |
|
| 15. |
Which of the following is a point on the curve y = x\(^2\) - 4x + 7? A. (0,6) B. (1,4) C. (2,0) D. (7,0) E. (3,2) |
B |
| 16. |
If 8x- 4 = 6x- 10, find the value of 5x, A. -35 B. -15 C. -3 D. 3 E. 7 Detailed Solution8x - 4 = 6x - 108x - 6x = -10 + 4 2x = -6 x = -3 \(\therefore\) 5x = 5(-3) = -15 |
|
| 17. |
For what value of x is the expression \(\frac{x^2 + 15x + 50}{x - 5}\) not defined ? A. -10 B. -5 C. o D. 5 E. 10 Detailed Solution\(\frac{x^2 + 15x + 50}{x - 5}\)It is undefined when x - 5 = 0. That is at x = 5. |
|
| 18. |
If x is positive, for what range of values of x is 4 + 3x < 10? A. 0 < x < 2 B. x < 2 C. 1 < x < 2 D. 0 < x < 4 3 4 E. 0 > x > 2 Detailed Solution4 + 3x < 103x < 10 - 4 3x < 6 x < 2 |
|
| 19. |
 In the graph above, the gradient of the curve at the point P is A. -11 3 B. -3 4 C. 3/7 D. 3/4 E. 11 3 Detailed Solution-1-(-3)/-2-(-0.5) = 2/-1.5 = 20/-15 = -113 |
|
| 20. |
 What is the equation of the line PQ? A. y = x - 5 B. y = x + 3 C. y = x + 5 D. y = 2x + 3 E. y = 2x - 3 Detailed SolutionThe points P(-2, 3) and Q(2, 7) are on the line.Gradient of the line = \(\frac{7 - 3}{2 - (-2)}\) = \(\frac{4}{4}\) = 1 y = x + b To find the intercept, we have 7 = 2 + b or 3 = -2 + b. Solving for b, we get b = 5. \(\therefore\) The line is y = x + 5. |