Year :
1985
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 47 of 47 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
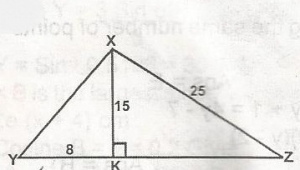 In \(\bigtriangleup\) XYZ, XKZ = 90O, XK = 15cm, XZ = 25cm and YK = 8cm. Find the area of \(\bigtriangleup\)XYZ A. 190 sq.cm B. 20 sq.cm C. 210 sq.cm D. 160sq.cm E. 320sq.cm Detailed SolutionBy Pythagoras, KZ2 = 252 - 52KZ2 = (25 + 15)(25 - 15) = 400 KZ = \(\sqrt{400}\) = 20 area of XYZ = \(\frac{1}{2} \times 28 \times 15\) = 210 sq. cm |
|
| 42. |
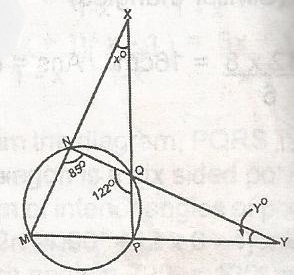 In the figure, MNQP is a cyclic quadrilateral. MN and Pq are produced to meet at X and NQ and MP are produced to meet at Y. If MNQ = 86o and NQP = 122o find (xo, yo) A. 28o, 36o B. 36o, 28o C. 43o, 61o D. 61o, 43o E. 36o, 43o Detailed Solutionyo = 180o - (86o + 58o)180 - 144 = 36o xo = 180 - (94 + 58) 180 -152 = 28 (xo, yo) = (28o, 36o) |
|
| 43. |
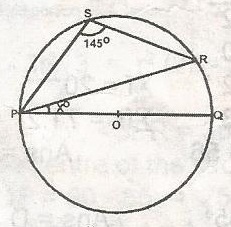
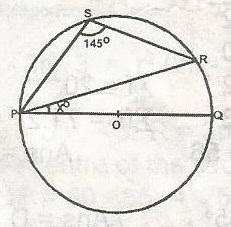 In the figure POQ is the diameter of the circle PQR. If PSR = 145o, find xo A. 25o B. 35o C. 45o D. 125o E. 55o Detailed Solution
< PSR + < PQR = 180o < PQR = 180o - 145o = 35o \(\bigtriangleup\)PQR is a right angled triangle x = 90 - < PQR = 90o - 35o = 55o |
|
| 44. |
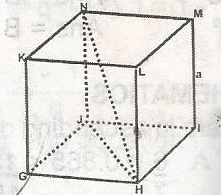 In the figure, GHIJKLMN is a cube of side a. Find the length of HN. A. \(\sqrt{3a}\) B. 3a C. 3a2 D. a\(\sqrt{2}\) E. a\(\sqrt{3}\) Detailed SolutionHJ2 = a2 + a2 = 2a2HJ = \(\sqrt{2a^2} = a \sqrt{2}\) HN2 = a2 + (a\(\sqrt{2}\))2 = a2 + 2a2 = 3a2 HN = \(\sqrt{3a^2}\) = a\(\sqrt{3}\)cm |
|
| 45. |
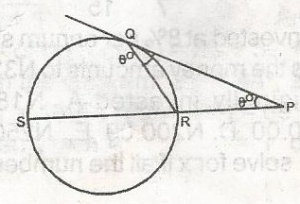 In the figure, PQ is the tangent from P to the circle QRS with SR as its diameter. If QRS = \(\theta\)oand RQP = \(\phi\)o, which of the following relationships between \(\theta\)o and \(\phi\)o is correct A. \(\theta\)o + \(\phi\)o = 902 B. \(\phi\)o = 902 - 2\(\theta\)o C. \(\theta\)o = \(\phi\)o D. \(\phi\)o = 2\(\theta\)o E. \(\theta\)o + 2\(\phi\)o Detailed Solution180 - \(\phi\)o = \(\theta\)o + \(\phi\)o (Sum of opposite interior angle equal to its exterior angle)180 = 2\(\phi\) + \(\theta\)o |
|
| 46. |
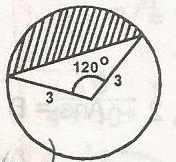
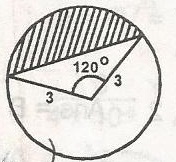 In the figure, the area of the shaded segment is A. 3\(\pi\) B. 9\(\frac{\sqrt{3}}{4}\) C. 3 \(\pi - 3 \frac{\sqrt{3}}{4}\) D. \(\frac{(\sqrt{3 - \pi)}}{4}\) E. \(\pi + \frac{9 \sqrt{3}}{4}\) Detailed Solution
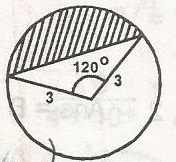 Area of triangle = \(\frac{1}{2} \times 3 \times 3 \times \sin 120^o\) = \(\frac{9}{2} \times \frac{\sqrt{3}}{2} = \frac{9\sqrt {3}}{4}\) Area of shaded portion = 3\(\pi - \frac{9\sqrt {3}}{4}\) = 3 \(\pi - 3 \frac{\sqrt{3}}{4}\) |
|
| 47. |
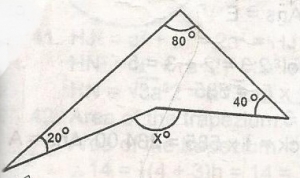 In the figure, find angle x A. 100o B. 120o C. 60o D. 110o E. 140o Detailed SolutionIn the figure, angle x = 20o + 80o + 40o= 140o |
| 41. |
 In \(\bigtriangleup\) XYZ, XKZ = 90O, XK = 15cm, XZ = 25cm and YK = 8cm. Find the area of \(\bigtriangleup\)XYZ A. 190 sq.cm B. 20 sq.cm C. 210 sq.cm D. 160sq.cm E. 320sq.cm Detailed SolutionBy Pythagoras, KZ2 = 252 - 52KZ2 = (25 + 15)(25 - 15) = 400 KZ = \(\sqrt{400}\) = 20 area of XYZ = \(\frac{1}{2} \times 28 \times 15\) = 210 sq. cm |
|
| 42. |
 In the figure, MNQP is a cyclic quadrilateral. MN and Pq are produced to meet at X and NQ and MP are produced to meet at Y. If MNQ = 86o and NQP = 122o find (xo, yo) A. 28o, 36o B. 36o, 28o C. 43o, 61o D. 61o, 43o E. 36o, 43o Detailed Solutionyo = 180o - (86o + 58o)180 - 144 = 36o xo = 180 - (94 + 58) 180 -152 = 28 (xo, yo) = (28o, 36o) |
|
| 43. |
 In the figure POQ is the diameter of the circle PQR. If PSR = 145o, find xo A. 25o B. 35o C. 45o D. 125o E. 55o Detailed Solution
< PSR + < PQR = 180o < PQR = 180o - 145o = 35o \(\bigtriangleup\)PQR is a right angled triangle x = 90 - < PQR = 90o - 35o = 55o |
|
| 44. |
 In the figure, GHIJKLMN is a cube of side a. Find the length of HN. A. \(\sqrt{3a}\) B. 3a C. 3a2 D. a\(\sqrt{2}\) E. a\(\sqrt{3}\) Detailed SolutionHJ2 = a2 + a2 = 2a2HJ = \(\sqrt{2a^2} = a \sqrt{2}\) HN2 = a2 + (a\(\sqrt{2}\))2 = a2 + 2a2 = 3a2 HN = \(\sqrt{3a^2}\) = a\(\sqrt{3}\)cm |
| 45. |
 In the figure, PQ is the tangent from P to the circle QRS with SR as its diameter. If QRS = \(\theta\)oand RQP = \(\phi\)o, which of the following relationships between \(\theta\)o and \(\phi\)o is correct A. \(\theta\)o + \(\phi\)o = 902 B. \(\phi\)o = 902 - 2\(\theta\)o C. \(\theta\)o = \(\phi\)o D. \(\phi\)o = 2\(\theta\)o E. \(\theta\)o + 2\(\phi\)o Detailed Solution180 - \(\phi\)o = \(\theta\)o + \(\phi\)o (Sum of opposite interior angle equal to its exterior angle)180 = 2\(\phi\) + \(\theta\)o |
|
| 46. |
 In the figure, the area of the shaded segment is A. 3\(\pi\) B. 9\(\frac{\sqrt{3}}{4}\) C. 3 \(\pi - 3 \frac{\sqrt{3}}{4}\) D. \(\frac{(\sqrt{3 - \pi)}}{4}\) E. \(\pi + \frac{9 \sqrt{3}}{4}\) Detailed Solution
 Area of triangle = \(\frac{1}{2} \times 3 \times 3 \times \sin 120^o\) = \(\frac{9}{2} \times \frac{\sqrt{3}}{2} = \frac{9\sqrt {3}}{4}\) Area of shaded portion = 3\(\pi - \frac{9\sqrt {3}}{4}\) = 3 \(\pi - 3 \frac{\sqrt{3}}{4}\) |
|
| 47. |
 In the figure, find angle x A. 100o B. 120o C. 60o D. 110o E. 140o Detailed SolutionIn the figure, angle x = 20o + 80o + 40o= 140o |