Year :
1993
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
31 - 40 of 51 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
If two angles of a triangle are 30° each and the longest side is 10cm. Calculate the length of each of the other sides. A. 5cm B. 4cm C. 3√3 cm D. \(\frac{10\sqrt{3}}{3}\)cm Detailed SolutionLet each of the unknown side be x.\(10^{2} = x^{2} + x^{2} - 2(x)(x) \cos 120\) \(100 = 2x^{2} - 2x^{2} \cos 120\) \(100 = 2x^{2} + x^{2} = 3x^{2}\) x = \(\sqrt{\frac{100}{3}}\) = \(\frac{10}{\sqrt{3}}\) x \(\frac{\sqrt{3}}{\sqrt{3}}\) x = \(\frac{10\sqrt{3}}{3}\)cm |
|
| 32. |
Quantities in the proportions 1, 4, 6, 7 are to be represented in a pie chart. Calculate the angle of the sector with proportion 7 A. 20o B. 80o C. 120o D. 140o Detailed SolutionAngle corresponding to 7 in a pie chart will be \(\frac{7 \times 360}{\text{sum of items}}\)= \(\frac{7 }{18}\) x 360 = 140o |
|
| 33. |
The following marks were obtained by twenty students in an examination: 53, 30, 70, 84, 59, 43, 90, 20, 78, 48, 44, 60, 81, 73, 50, 37, 67, 68, 64, 52. Find the numbers of students who scored at least 50 marks A. 6 B. 10 C. 13 D. 14 Detailed SolutionNumber of students scoring at least 50 marks = Number of students scoring 50 and aboveFrom the table 53, 70, 84, 59, 90, 60, 81, 73, 50, 37, 67, 68, 64, 52. Hence, 14 students scored at least 50 marks |
|
| 34. |
\(\begin{array}{c|c} Weight(s) & 0 -10 & 10 - 20 & 20 - 30 & 40 - 50\\ \hline \text{Number of coconuts} & 10 & 27 & 19 & 6 & 2\end{array}\) A. 13.2g B. 15.0g C. 16.8g D. 17.5g Detailed SolutionMode = a + \(\frac{(b - a)(F_m - F_b)}{2F_m - F_a - F_b}\)= \(L_1 + \frac{\Delta_1 x^\text{c}}{\Delta_1 + \Delta_2}\) = \(10 + \frac{(20 - 10)(27 - 10)}{2(27) - 10 - 19}\) = 10 + \(\frac{170}{25}\) = 10 + 6.8 = 16.8 |
|
| 35. |
The mean of the ages of ten secondary school pupils is 16 but when the age of their teacher is added to it the men becomes 19. Find the age of the teacher A. 27 B. 35 C. 38 D. 49 Detailed SolutionAverage age of 110 students = 16∴ Total age = 16 x 10 = 160 years Age of teachers = x, total number of people now = 11 mean age = 19 Total age of new group = 19 x 11 = 209 Age of teachers = x = (209 - 160) = 49 yrs |
|
| 36. |
\(\begin{array}{c|c} Class & Frequency\\ \hline 1 - 5 & 2\\6 - 10 & 4\\11 - 15 & 5\\16 - 20 & 2 \\ 21 - 25 & 3\\26 - 30 & 2\\31 - 35 & 1\\36 - 40 & 1 \end{array}\) A. 11.5 B. 12.5 C. 14.0 D. 14.5 Detailed SolutionMedian = L1 + (\(\frac{Ef}{fm}\)) - fo\(\frac{\sum f}{2}\) = \(\frac{20}{2}\) = 10, L1 = 10.5, fo = 6, fm = 5 Median = 10.5 + \(\frac{(10 - 6)}{5}\)5 = 10.5 + 4 = 14.5 |
|
| 37. |
A number is selected at random between 20 and 30, both numbers inclusive. Find the probability that the number is a prime A. \(\frac{2}{11}\) B. \(\frac{5}{11}\) C. \(\frac{6}{11}\) D. \(\frac{8}{11}\) Detailed SolutionPossible outcomes are 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30. Prime numbers has only two factorsitself and 1 The prime numbers among the group are 23, 29. Probability of choosing a prime number = \(\frac{\text{Number of prime}}{\text{No. of total Possible Outcomes}}\) = \(\frac{2}{11}\) |
|
| 38. |
Calculate the standard deviation of the following data: 7, 8, 9, 10, 11, 12, 13. A. 2 B. 4 C. 10 D. 11 Detailed Solution\(\begin{array}{c|c} x & x - x & (x - x)^2\\ \hline 7 & -3 & 9\\8 & -2 & 4 \\9 & -1 & 1\\10 & 0 & 1\\11 & 1 & 1\\ 12 & 2 & 4\\13 & 3 & 9\\ \hline & & 28\end{array}\)S.D = \(\sqrt{\frac{\sum(x - x)^2}{N}}\) = \(\sqrt{\frac{\sum d^2}{N}}\) = \(\sqrt{\frac{28}{7}}\) = \(\sqrt{4}\) = 2 |
|
| 39. |
The chances of three independent events X, Y, Z occurring are \(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{1}{4}\) respectively. What are the chances of Y and Z only occurring? A. \(\frac{1}{8}\) B. \(\frac{1}{24}\) C. \(\frac{1}{12}\) D. \(\frac{1}{4}\) Detailed SolutionChance of x = \(\frac{1}{2}\)Change of Y = \(\frac{2}{3}\) Chance of Z = \(\frac{1}{4}\) Chance of Y and Z only occurring = Pr (Y ∩ Z ∩ Xc) where Xc = 1 - Pr(X) 1 - \(\frac{1}{2}\) = \(\frac{1}{2}\) = Pr(Y) x Pr(Z) x Pr(Xc) = \(\frac{2}{3}\) x \(\frac{1}{4}\) x \(\frac{1}{2}\) = \(\frac{1}{12}\) |
|
| 40. |
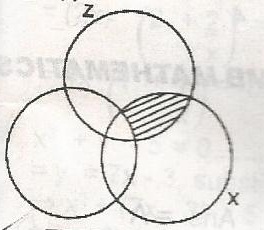 The shaded portion in the venn diagram is A. x \(\cap\) z B. xo \(\cap\) y \(\cap\) z C. x \(\cap\) yo \(\cap\) z D. x \(\cap\) y \(\cap\) zo Detailed SolutionThe shaded part exists on x \(\cap\) z but not in y |
| 31. |
If two angles of a triangle are 30° each and the longest side is 10cm. Calculate the length of each of the other sides. A. 5cm B. 4cm C. 3√3 cm D. \(\frac{10\sqrt{3}}{3}\)cm Detailed SolutionLet each of the unknown side be x.\(10^{2} = x^{2} + x^{2} - 2(x)(x) \cos 120\) \(100 = 2x^{2} - 2x^{2} \cos 120\) \(100 = 2x^{2} + x^{2} = 3x^{2}\) x = \(\sqrt{\frac{100}{3}}\) = \(\frac{10}{\sqrt{3}}\) x \(\frac{\sqrt{3}}{\sqrt{3}}\) x = \(\frac{10\sqrt{3}}{3}\)cm |
|
| 32. |
Quantities in the proportions 1, 4, 6, 7 are to be represented in a pie chart. Calculate the angle of the sector with proportion 7 A. 20o B. 80o C. 120o D. 140o Detailed SolutionAngle corresponding to 7 in a pie chart will be \(\frac{7 \times 360}{\text{sum of items}}\)= \(\frac{7 }{18}\) x 360 = 140o |
|
| 33. |
The following marks were obtained by twenty students in an examination: 53, 30, 70, 84, 59, 43, 90, 20, 78, 48, 44, 60, 81, 73, 50, 37, 67, 68, 64, 52. Find the numbers of students who scored at least 50 marks A. 6 B. 10 C. 13 D. 14 Detailed SolutionNumber of students scoring at least 50 marks = Number of students scoring 50 and aboveFrom the table 53, 70, 84, 59, 90, 60, 81, 73, 50, 37, 67, 68, 64, 52. Hence, 14 students scored at least 50 marks |
|
| 34. |
\(\begin{array}{c|c} Weight(s) & 0 -10 & 10 - 20 & 20 - 30 & 40 - 50\\ \hline \text{Number of coconuts} & 10 & 27 & 19 & 6 & 2\end{array}\) A. 13.2g B. 15.0g C. 16.8g D. 17.5g Detailed SolutionMode = a + \(\frac{(b - a)(F_m - F_b)}{2F_m - F_a - F_b}\)= \(L_1 + \frac{\Delta_1 x^\text{c}}{\Delta_1 + \Delta_2}\) = \(10 + \frac{(20 - 10)(27 - 10)}{2(27) - 10 - 19}\) = 10 + \(\frac{170}{25}\) = 10 + 6.8 = 16.8 |
|
| 35. |
The mean of the ages of ten secondary school pupils is 16 but when the age of their teacher is added to it the men becomes 19. Find the age of the teacher A. 27 B. 35 C. 38 D. 49 Detailed SolutionAverage age of 110 students = 16∴ Total age = 16 x 10 = 160 years Age of teachers = x, total number of people now = 11 mean age = 19 Total age of new group = 19 x 11 = 209 Age of teachers = x = (209 - 160) = 49 yrs |
| 36. |
\(\begin{array}{c|c} Class & Frequency\\ \hline 1 - 5 & 2\\6 - 10 & 4\\11 - 15 & 5\\16 - 20 & 2 \\ 21 - 25 & 3\\26 - 30 & 2\\31 - 35 & 1\\36 - 40 & 1 \end{array}\) A. 11.5 B. 12.5 C. 14.0 D. 14.5 Detailed SolutionMedian = L1 + (\(\frac{Ef}{fm}\)) - fo\(\frac{\sum f}{2}\) = \(\frac{20}{2}\) = 10, L1 = 10.5, fo = 6, fm = 5 Median = 10.5 + \(\frac{(10 - 6)}{5}\)5 = 10.5 + 4 = 14.5 |
|
| 37. |
A number is selected at random between 20 and 30, both numbers inclusive. Find the probability that the number is a prime A. \(\frac{2}{11}\) B. \(\frac{5}{11}\) C. \(\frac{6}{11}\) D. \(\frac{8}{11}\) Detailed SolutionPossible outcomes are 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30. Prime numbers has only two factorsitself and 1 The prime numbers among the group are 23, 29. Probability of choosing a prime number = \(\frac{\text{Number of prime}}{\text{No. of total Possible Outcomes}}\) = \(\frac{2}{11}\) |
|
| 38. |
Calculate the standard deviation of the following data: 7, 8, 9, 10, 11, 12, 13. A. 2 B. 4 C. 10 D. 11 Detailed Solution\(\begin{array}{c|c} x & x - x & (x - x)^2\\ \hline 7 & -3 & 9\\8 & -2 & 4 \\9 & -1 & 1\\10 & 0 & 1\\11 & 1 & 1\\ 12 & 2 & 4\\13 & 3 & 9\\ \hline & & 28\end{array}\)S.D = \(\sqrt{\frac{\sum(x - x)^2}{N}}\) = \(\sqrt{\frac{\sum d^2}{N}}\) = \(\sqrt{\frac{28}{7}}\) = \(\sqrt{4}\) = 2 |
|
| 39. |
The chances of three independent events X, Y, Z occurring are \(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{1}{4}\) respectively. What are the chances of Y and Z only occurring? A. \(\frac{1}{8}\) B. \(\frac{1}{24}\) C. \(\frac{1}{12}\) D. \(\frac{1}{4}\) Detailed SolutionChance of x = \(\frac{1}{2}\)Change of Y = \(\frac{2}{3}\) Chance of Z = \(\frac{1}{4}\) Chance of Y and Z only occurring = Pr (Y ∩ Z ∩ Xc) where Xc = 1 - Pr(X) 1 - \(\frac{1}{2}\) = \(\frac{1}{2}\) = Pr(Y) x Pr(Z) x Pr(Xc) = \(\frac{2}{3}\) x \(\frac{1}{4}\) x \(\frac{1}{2}\) = \(\frac{1}{12}\) |
|
| 40. |
 The shaded portion in the venn diagram is A. x \(\cap\) z B. xo \(\cap\) y \(\cap\) z C. x \(\cap\) yo \(\cap\) z D. x \(\cap\) y \(\cap\) zo Detailed SolutionThe shaded part exists on x \(\cap\) z but not in y |