Mathematics (Core)
Paper 1 | Objectives | 50 Questions
JAMB Exam
Year: 2006
Level: SHS
Time:
Type: Question Paper
Answers provided
FREE
No description provided
Feedbacks
This paper is yet to be rated
Paper 1 | Objectives | 50 Questions
JAMB Exam
Year: 2006
Level: SHS
Time:
Type: Question Paper
Answers provided
No description provided
This paper is yet to be rated
| # | Question | Ans |
|---|---|---|
| 1. |
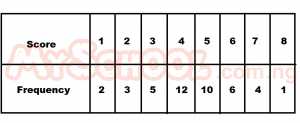 The table above shows the scores of a group of students in a physics test. If the mode is m and the number of students who scored 4 or more is n, what is (n, m)? A. (33, 4) B. (22, 4) C. (33, 12) D. (12, 4) Detailed SolutionThe mode (m) = 4.No of students who scored 4 and above = 12 + 10 + 6 + 4 + 1 = 33. \(\therefore\) (n, m) = (33, 4) |
|
| 2. |
A final examination requires that a student answer any 4 out of 6 questions. In how many ways can this be done? A. 15 B. 20 C. 30 D. 45 Detailed SolutionThe question will be answered in\(^5C_4 = \frac{6!}{(6-4)!4!}\\=\frac{6!}{2!4!}\\=\frac{6\times5\times4!}{2\times1\times4!}\\=15\hspace{1mm}ways\) |
|
| 3. |
If the mean of five consecutive integers is 30, find the largest of the numbers A. 28 B. 30 C. 32 D. 34 Detailed SolutionLet the consecutive numbers be a, a+1, a+2, a+3, a+4Mean = \(\frac{(a+a+1+a+2+a+3+a+4)}{5}\\ 30 = \frac{5a+10}{5}\\ 30 \times 5 = 5a + 10\\ 5a = 150 - 10\\ 5a = 140\\ a = 28 \\ ∴ a + 4 = 28 + 4\\ = 32\) |
|
| 4. |
A bag contains 5 black, 4 white and x red marbles. If the probability of picking a red marble is 2/3, find the value of x A. 8 B. 10 C. 4 D. 6 Detailed SolutionBlack = 5White = 4 Red = x Total = 9+x P(red) = 2/3 x / (9+x) = 2/5 5x = 2(9+x) 5x = 18+2x 5x-2 = 18 3x = 18 x = 6 |
|
| 5. |
Find the variance of 2x, 2x-1 and 2x+1 A. 2/3 B. 2 C. √(2/3) D. 1 Detailed Solution
 \sum(x-\bar{x})^2 = 2\\ \bar{x} = \frac{\sum x}{n}\\ = \frac{6x}{3}\\ = 2x\\ Variance = \frac{\sum(x-\bar{x})^2}{n}\\ = \frac{2}{3}\) |
|
| 6. |
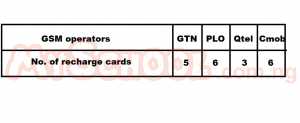 The table above shows the distribution of recharge cards of four major GSM operators. What is the probability that a recharge card selected at random will be GTN or Qtel? A. 3/20 B. 1/4 C. 2/5 D. 3/4 Detailed SolutionP(GTN) = 5/20P(Qtel) = 3/20 ∴P(GTN or Qtel) = (5/20) + (3/20) = 8/20 = 2/5 |
|
| 7. |
 The pie chart above shows the expenditure of a family whose income is N30,000. If the expenditure on food is twice that on housing and that on school fees is twice that on transport, how much does the family spend on food? A. N 28 000 B. N 25 500 C. N15 000 D. N 12 500 Detailed SolutionExpenditure on housing = xExpenditure on food = 2x Expenditure on school fees = 90o Expenditure on transport = 45o x + 2x + 90 + 45 = 360o 3x + 135 = 360o 3x = 360 - 135 3x = 225 x = 225/3 = 75o ∴∠ for food = 2x = 2 * 75 = 150 360o = N30,000 1o = ? 1o = 30,000/360 150o = (30000/360) * (150/1) = N12500 |
|
| 8. |
For what of n is n+1C3 = 4(nC3)? A. 6 B. 5 C. 4 D. 3 Detailed Solution\(^{n+1}C_3 = 4(^nC_3)\\\frac{(n+1)!}{(n+1-3)!3!} = 4\left(\frac{n!}{(n-3)!3!}\right)\\\frac{(n+1)n!}{(n-2)(n-3)!}=4\left(\frac{n!}{n-3!}\right)\\=\frac{n+1}{n-2}=\frac{4}{1}\\n+1 = 4(n-2)\\n+1 = 4n-8\\-3n = -9\\\frac{-9}{-3}\\n=3\) |
|
| 9. |
The gradient of a curve is 2x + 7 and the curve passes through point (2, 0). find the equation of the curve. A. y = x2 + 7x + 9 B. y = x2 + 7x - 18 C. y = x2 + 7x + 18 D. y = x2 + 14x + 11 Detailed Solutiondy/dx = 2x + 7y = ∫2x + 7 y = x2 + 7x + C at (2,0) 0 = 22 + 7(2) + C 0 = 4 + 14 + C 0 = 18 + C C = -18 ∴ The equation is y = x2 + 7x - 18 |
|
| 10. |
Differentiate (x2 - 1/x)2 with respect to x A. 4x2 - 4x - 2/x B. 4x2 - 2 + 2/x3 C. 4x2 - 2 - 2/x3 D. 4x2 - 3x + 2/x Detailed Solutiony = (x2 - 1/x)2y = (x2 - 1/x)(x2 - 1/x) y = x4 - x - x + 1/x2 y = x4 - 2x + 1/x2 y= x4 - 2x + x-2 dy/dx = 4x2 - 2 - 2x-3 = 4x2 - 2 - 2 |
Preview displays only 10 out of the 50 Questions
