Year :
1982
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 48 of 48 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
The arithmetic mean of the ages of 30 pupils in a class is 15.3 years. One boy leaves the class and one girl is enrolled, and the new average age of 30 pupils in the class becomes 15.2 years. How much older is the boy than the girl? A. 30 years B. 6 years C. 9 years D. 3 years E. 1 year Detailed Solution1st 30 pupils at average age of 15.3 yrs. give total age of 15.3 x 30 = 459yrs2nd group of 30 pupils at average age of 15.2 yrs give total age of 15.2 x 30 = 456yrs Difference in age = 459 - 456 = 3 yrs |
|
| 42. |
 In the diagram, angle QPR = 90o, angle PSR = 90o and PR = 5 units. Find the length of QS. A. 5 tan 25o sin 65o B. 5 cos 25o sin 65o C. 5 tan 25o cos 65o D. cos 25o cos 65o E. 5 cosec 25o Detailed SolutionFrom \(\bigtriangleup\)QPR, < R = 180o - (25o + 90o)180o - 115o = 65o From \(\bigtriangleup\)PSQ, Sin 65o = \(\frac{QPR}{hyp}\) = \(\frac{PS}{5}\) PS = 5 sin 65o From \(\bigtriangleup\)PSR, tan = \(\frac{OPP}{adj}\) = \(\frac{PS}{QS}\) but PS = 5 sin 65o QS tan 25o = PS QS tan 25o = 5 sin 65o QS = |
|
| 43. |
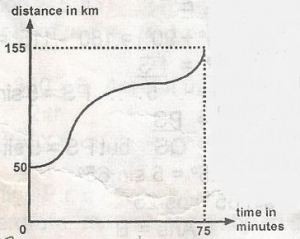 The diagram is the distance time graph of a vehicle. Find its average speed in kilometers per hour during the journey A. 155km/hr B. 50km/hr C. 40km/hr D. 124km/hr E. 84km/hr Detailed SolutionDistance = 155 - 50 = 105kmTime = 75mins = \(\frac{75}{60}\)hr = \(\frac{5}{4}\)hr Average speed = \(\frac{Distance}{time}\) = \(\frac{105}{\frac{5}{4}}\) = \(\frac{105 \times 4}{5}\) = 84km\h |
|
| 44. |
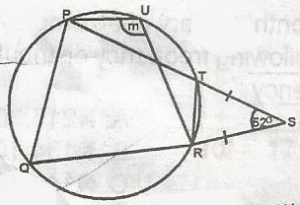 In the fiqure where PQRTU is a circle, ISTI = IRSI and angle TSR = 52o. Find the angle marked m A. 128o B. 52o C. 104o D. 64o E. 116o Detailed Solution< STR = \(\frac{180 - 52}{2}\) = \(\frac{128}{2}\) = 64o< PTR = 180 - < STR(angle on a straight line) = 180 - 64 = 116o < PQR + < PTR = 180(Supplementary) < PQR + 118 = 180 < PQR = 180 - 118 = 64 M = 180 - < PQR = 180 - < PQR = 180 - 64 = 116o |
|
| 45. |
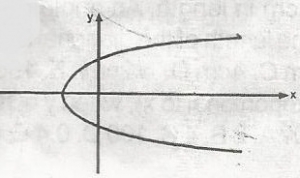 If K is a constant, which of the following equations best describes the parabola? A. y = kx2 B. x = y2 - k C. y = k - x2 D. x2 = y2 - k E. y = (k - x)2 Detailed SolutionThe parabola is best described by the equation x = y2 - k because all other equations do not give the equation of the parabola in this position. C for example is the equation of a hyperbola facing downwards. D is the equation of a hyperbola A and E are equations of parabola facing upwards |
|
| 46. |
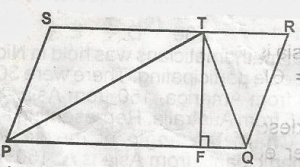 PQRS is a parallelogram with area 50 square cm and the side PQ is 10cm long. T is a point on RS and TF is the altitude of the triangle TPQ. Find TF A. 10cm B. 12.5cm C. 8cm D. 6cm E. 5cm Detailed SolutionArea of a //gm PQRS = B X HArea of a //gm PQRS = PQ x TF 50 = 10TF TF = 5cm |
|
| 47. |
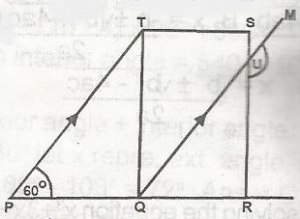 In the figure, QRST is a rectangle; PT// QM, angle P = 60o. Find angle MUR A. 150o B. 30o C. 60o D. 120o E. 90o Detailed SolutionQRST is a rectanglePT //QM, P = 60o = angle MUR = 150o |
|
| 48. |
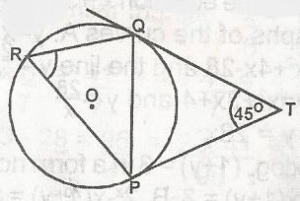 TP and TQ are tangents to a circle centre 0 and r is a point on the circumference of the circle as shown in the figure. If angle PTQ = 45o, what is the magnitude of the angle PRO? A. 45 B. 135 C. 40 D. 76\(\frac{1}{2}\) E. 52\(\frac{1}{2}\) Detailed SolutionPTQ = 45o< PRQ = 76\(\frac{1}{2}\) |
| 41. |
The arithmetic mean of the ages of 30 pupils in a class is 15.3 years. One boy leaves the class and one girl is enrolled, and the new average age of 30 pupils in the class becomes 15.2 years. How much older is the boy than the girl? A. 30 years B. 6 years C. 9 years D. 3 years E. 1 year Detailed Solution1st 30 pupils at average age of 15.3 yrs. give total age of 15.3 x 30 = 459yrs2nd group of 30 pupils at average age of 15.2 yrs give total age of 15.2 x 30 = 456yrs Difference in age = 459 - 456 = 3 yrs |
|
| 42. |
 In the diagram, angle QPR = 90o, angle PSR = 90o and PR = 5 units. Find the length of QS. A. 5 tan 25o sin 65o B. 5 cos 25o sin 65o C. 5 tan 25o cos 65o D. cos 25o cos 65o E. 5 cosec 25o Detailed SolutionFrom \(\bigtriangleup\)QPR, < R = 180o - (25o + 90o)180o - 115o = 65o From \(\bigtriangleup\)PSQ, Sin 65o = \(\frac{QPR}{hyp}\) = \(\frac{PS}{5}\) PS = 5 sin 65o From \(\bigtriangleup\)PSR, tan = \(\frac{OPP}{adj}\) = \(\frac{PS}{QS}\) but PS = 5 sin 65o QS tan 25o = PS QS tan 25o = 5 sin 65o QS = |
|
| 43. |
 The diagram is the distance time graph of a vehicle. Find its average speed in kilometers per hour during the journey A. 155km/hr B. 50km/hr C. 40km/hr D. 124km/hr E. 84km/hr Detailed SolutionDistance = 155 - 50 = 105kmTime = 75mins = \(\frac{75}{60}\)hr = \(\frac{5}{4}\)hr Average speed = \(\frac{Distance}{time}\) = \(\frac{105}{\frac{5}{4}}\) = \(\frac{105 \times 4}{5}\) = 84km\h |
|
| 44. |
 In the fiqure where PQRTU is a circle, ISTI = IRSI and angle TSR = 52o. Find the angle marked m A. 128o B. 52o C. 104o D. 64o E. 116o Detailed Solution< STR = \(\frac{180 - 52}{2}\) = \(\frac{128}{2}\) = 64o< PTR = 180 - < STR(angle on a straight line) = 180 - 64 = 116o < PQR + < PTR = 180(Supplementary) < PQR + 118 = 180 < PQR = 180 - 118 = 64 M = 180 - < PQR = 180 - < PQR = 180 - 64 = 116o |
| 45. |
 If K is a constant, which of the following equations best describes the parabola? A. y = kx2 B. x = y2 - k C. y = k - x2 D. x2 = y2 - k E. y = (k - x)2 Detailed SolutionThe parabola is best described by the equation x = y2 - k because all other equations do not give the equation of the parabola in this position. C for example is the equation of a hyperbola facing downwards. D is the equation of a hyperbola A and E are equations of parabola facing upwards |
|
| 46. |
 PQRS is a parallelogram with area 50 square cm and the side PQ is 10cm long. T is a point on RS and TF is the altitude of the triangle TPQ. Find TF A. 10cm B. 12.5cm C. 8cm D. 6cm E. 5cm Detailed SolutionArea of a //gm PQRS = B X HArea of a //gm PQRS = PQ x TF 50 = 10TF TF = 5cm |
|
| 47. |
 In the figure, QRST is a rectangle; PT// QM, angle P = 60o. Find angle MUR A. 150o B. 30o C. 60o D. 120o E. 90o Detailed SolutionQRST is a rectanglePT //QM, P = 60o = angle MUR = 150o |
|
| 48. |
 TP and TQ are tangents to a circle centre 0 and r is a point on the circumference of the circle as shown in the figure. If angle PTQ = 45o, what is the magnitude of the angle PRO? A. 45 B. 135 C. 40 D. 76\(\frac{1}{2}\) E. 52\(\frac{1}{2}\) Detailed SolutionPTQ = 45o< PRQ = 76\(\frac{1}{2}\) |