Year :
2013
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 48 of 48 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
The locus of the points which is equidistant from the line PQ forms a A. perpendicular line to PQ B. circle centre P C. circle centre Q D. pair of parallel lines to PQ |
|
| 42. |
If the midpoint of the line PQ is (2,3) and the point P is (-2, 1), find the coordinate of the point Q. A. (8,6) B. (5,6) C. (0,4) D. (6,5) Detailed SolutionMidpoint of a line PQ where P has coordinates (x\(_{1}\), y\(_{1}\)) and Q has coordinates (x\(_{2}\), y\(_{2}\)) is given as\((\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})\). \(\therefore\) If Q has coordinates (r, s), then \(\frac{-2 + r}{2} = 2\) and \(\frac{1 + s}{2} = 3\) \(-2 + r = 4 \implies r = 6\) \(1 + s = 6 \implies s = 5\) Q = (6, 5) There is an explanation video available below. |
|
| 43. |
Find the equation of the perpendicular bisector of the line joining P(2, -3) to Q(-5, 1) A. 8y + 14x + 13 = 0 B. 8y - 14x + 13 = 0 C. 8y - 14x - 13 = 0 D. 8y + 14x - 13 = 0 Detailed SolutionGiven P(2, -3) and Q(-5, 1)Midpoint = \((\frac{2 + (-5)}{2}, \frac{-3 + 1}{2})\) = \((\frac{-3}{2}, -1)\) Slope of the line PQ = \(\frac{1 - (-3)}{-5 - 2}\) = \(-\frac{4}{7}\) The slope of the perpendicular line to PQ = \(\frac{-1}{-\frac{4}{7}}\) = \(\frac{7}{4}\) The equation of the perpendicular line: \(y = \frac{7}{4}x + b\) Using a point on the line (in this case, the midpoint) to find the value of b (the intercept). \(-1 = (\frac{7}{4})(\frac{-3}{2}) + b\) \(-1 + \frac{21}{8} = \frac{13}{8} = b\) \(\therefore\) The equation of the perpendicular bisector of the line PQ is \(y = \frac{7}{4}x + \frac{13}{8}\) \(\equiv 8y = 14x + 1 |
|
| 44. |
In triangle PQR, q = 8 cm, r = 6 cm and cos P = \(\frac{1}{12}\). Calculate the value of p. A. \(\sqrt{108}\) cm B. 9 cm C. \(\sqrt{92}\) cm D. 10 cm Detailed SolutionUsing the cosine rule, we have\(p^{2} = q^{2} + r^{2} - 2qr \cos P\) \(p^{2} = 8^{2} + 6^{2} - 2(8)(6)(\frac{1}{12})\) = \(64 + 36 - 8\) \(p^{2} = 92 \therefore p = \sqrt{92} cm\) There is an explanation video available below. |
|
| 45. |
If \(\tan \theta = \frac{3}{4}\), find the value of \(\sin \theta + \cos \theta\). A. \(1\frac{1}{3}\) B. \(1\frac{2}{3}\) C. \(1\frac{3}{5}\) D. \(1\frac{2}{5}\) Detailed Solution\(\tan \theta = \frac{opp}{adj} = \frac{3}{4}\)\(hyp^{2} = opp^{2} + adj^{2}\) \(hyp = \sqrt{3^{2} + 4^{2}}\) = 5 \(\sin \theta = \frac{3}{5}; \cos \theta = \frac{4}{5}\) \(\sin \theta + \cos \theta = \frac{3}{5} + \frac{4}{5}\) = \(\frac{7}{5} = 1\frac{2}{5}\) There is an explanation video available below. |
|
| 46. |
Integrate \(\frac{1 + x}{x^{3}} \mathrm d x\) A. \(2x^{2} - \frac{1}{x} + k\) B. \(-\frac{1}{2x^{2}} - \frac{1}{x} + k\) C. \(-\frac{x^{2}}{2} - \frac{1}{x} + k\) D. \(x^{2} - \frac{1}{x} + k\) Detailed Solution\(\int \frac{1 + x}{x^{3}} \mathrm d x\)= \(\int (\frac{1}{x^{3}} + \frac{x}{x^{3}}) \mathrm d x\) = \(\int (x^{-3} + x^{-2}) \mathrm d x\) = \(\frac{-1}{2x^{2}} - \frac{1}{x} + k\) There is an explanation video available below. |
|
| 47. |
Evaluate \(\int_{0} ^{\frac{\pi}{2}} \sin x \mathrm d x\) A. -2 B. 2 C. 1 D. -1 Detailed Solution\(\int_{0} ^{\frac{\pi}{2}} \sin x \mathrm d x\)= \(- \cos x |_{0} ^{\frac{\pi}{2}\) = \(- \cos (\frac{\pi}{2}) - (- \cos 0)\) = \(0 + 1\) = 1 There is an explanation video available below. |
|
| 48. |
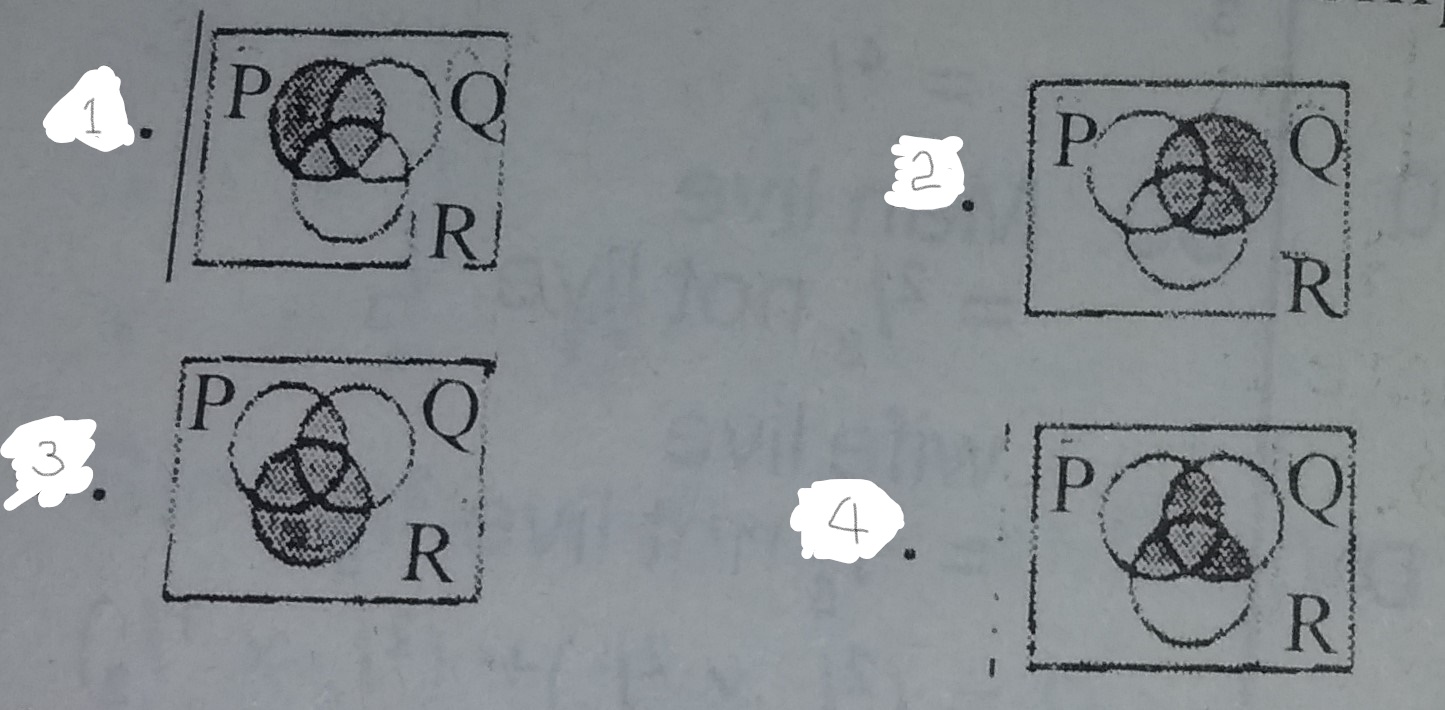 P, Q and R are subsets of the universal set U. The Venn diagram showing the relationship \((P \cap Q) \cup R\) is A. 1 B. 2 C. 3 D. 4 |
| 41. |
The locus of the points which is equidistant from the line PQ forms a A. perpendicular line to PQ B. circle centre P C. circle centre Q D. pair of parallel lines to PQ |
|
| 42. |
If the midpoint of the line PQ is (2,3) and the point P is (-2, 1), find the coordinate of the point Q. A. (8,6) B. (5,6) C. (0,4) D. (6,5) Detailed SolutionMidpoint of a line PQ where P has coordinates (x\(_{1}\), y\(_{1}\)) and Q has coordinates (x\(_{2}\), y\(_{2}\)) is given as\((\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})\). \(\therefore\) If Q has coordinates (r, s), then \(\frac{-2 + r}{2} = 2\) and \(\frac{1 + s}{2} = 3\) \(-2 + r = 4 \implies r = 6\) \(1 + s = 6 \implies s = 5\) Q = (6, 5) There is an explanation video available below. |
|
| 43. |
Find the equation of the perpendicular bisector of the line joining P(2, -3) to Q(-5, 1) A. 8y + 14x + 13 = 0 B. 8y - 14x + 13 = 0 C. 8y - 14x - 13 = 0 D. 8y + 14x - 13 = 0 Detailed SolutionGiven P(2, -3) and Q(-5, 1)Midpoint = \((\frac{2 + (-5)}{2}, \frac{-3 + 1}{2})\) = \((\frac{-3}{2}, -1)\) Slope of the line PQ = \(\frac{1 - (-3)}{-5 - 2}\) = \(-\frac{4}{7}\) The slope of the perpendicular line to PQ = \(\frac{-1}{-\frac{4}{7}}\) = \(\frac{7}{4}\) The equation of the perpendicular line: \(y = \frac{7}{4}x + b\) Using a point on the line (in this case, the midpoint) to find the value of b (the intercept). \(-1 = (\frac{7}{4})(\frac{-3}{2}) + b\) \(-1 + \frac{21}{8} = \frac{13}{8} = b\) \(\therefore\) The equation of the perpendicular bisector of the line PQ is \(y = \frac{7}{4}x + \frac{13}{8}\) \(\equiv 8y = 14x + 1 |
|
| 44. |
In triangle PQR, q = 8 cm, r = 6 cm and cos P = \(\frac{1}{12}\). Calculate the value of p. A. \(\sqrt{108}\) cm B. 9 cm C. \(\sqrt{92}\) cm D. 10 cm Detailed SolutionUsing the cosine rule, we have\(p^{2} = q^{2} + r^{2} - 2qr \cos P\) \(p^{2} = 8^{2} + 6^{2} - 2(8)(6)(\frac{1}{12})\) = \(64 + 36 - 8\) \(p^{2} = 92 \therefore p = \sqrt{92} cm\) There is an explanation video available below. |
| 45. |
If \(\tan \theta = \frac{3}{4}\), find the value of \(\sin \theta + \cos \theta\). A. \(1\frac{1}{3}\) B. \(1\frac{2}{3}\) C. \(1\frac{3}{5}\) D. \(1\frac{2}{5}\) Detailed Solution\(\tan \theta = \frac{opp}{adj} = \frac{3}{4}\)\(hyp^{2} = opp^{2} + adj^{2}\) \(hyp = \sqrt{3^{2} + 4^{2}}\) = 5 \(\sin \theta = \frac{3}{5}; \cos \theta = \frac{4}{5}\) \(\sin \theta + \cos \theta = \frac{3}{5} + \frac{4}{5}\) = \(\frac{7}{5} = 1\frac{2}{5}\) There is an explanation video available below. |
|
| 46. |
Integrate \(\frac{1 + x}{x^{3}} \mathrm d x\) A. \(2x^{2} - \frac{1}{x} + k\) B. \(-\frac{1}{2x^{2}} - \frac{1}{x} + k\) C. \(-\frac{x^{2}}{2} - \frac{1}{x} + k\) D. \(x^{2} - \frac{1}{x} + k\) Detailed Solution\(\int \frac{1 + x}{x^{3}} \mathrm d x\)= \(\int (\frac{1}{x^{3}} + \frac{x}{x^{3}}) \mathrm d x\) = \(\int (x^{-3} + x^{-2}) \mathrm d x\) = \(\frac{-1}{2x^{2}} - \frac{1}{x} + k\) There is an explanation video available below. |
|
| 47. |
Evaluate \(\int_{0} ^{\frac{\pi}{2}} \sin x \mathrm d x\) A. -2 B. 2 C. 1 D. -1 Detailed Solution\(\int_{0} ^{\frac{\pi}{2}} \sin x \mathrm d x\)= \(- \cos x |_{0} ^{\frac{\pi}{2}\) = \(- \cos (\frac{\pi}{2}) - (- \cos 0)\) = \(0 + 1\) = 1 There is an explanation video available below. |
|
| 48. |
 P, Q and R are subsets of the universal set U. The Venn diagram showing the relationship \((P \cap Q) \cup R\) is A. 1 B. 2 C. 3 D. 4 |