Year :
2013
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
31 - 40 of 48 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
A basket contains 9 apples, 8 bananas and 7 oranges. A fruit is picked from the basket, find the probability that it is neither an apple nor an orange. A. \(\frac{3}{8}\) B. \(\frac{1}{3}\) C. \(\frac{7}{24}\) D. \(\frac{2}{3}\) Detailed Solutionn(apples) = 9n(bananas) = 8 n(oranges) = 7 n(\(\varepsilon\)) = 24 Hence Prob(not apple, nor orange) = Prob(banana) = \(\frac{8}{24}\) = \(\frac{1}{3}\) There is an explanation video available below. |
|
| 32. |
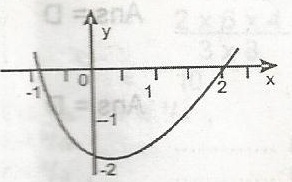 The graph above is correctly represented by A. y = x2 - x - 2 B. y = x2 - 3x + 2 C. y = x2 - x - 1 D. y = x2 + x - 2 Detailed SolutionThe graph crosses the x-axis at x = -1 and x = 2Thus, x + 1 = 0 and x - 2 = 0 x\(^2\) - 2x + x - 2 = 0 x\(^2\) - x - 2 = 0 giving y = x\(^2\) - x - 2 There is an explanation video available below. |
|
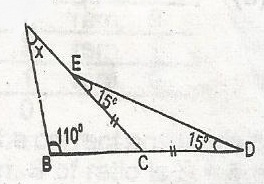
| 33. |
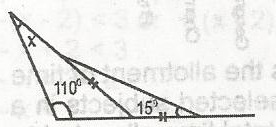 In the diagram given, find the value of x. A. 30o B. 40o C. 45o D. 15o |
|
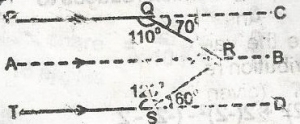
| 34. |
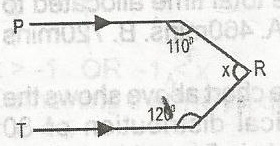 The value x in the figure given is A. 110o B. 100o C. 70o D. 130o Detailed Solution
180° - x + 60 + 70 = 180 130° - x = 180° - 180° = 0° x = 130° There is an explanation video available below. |
|
| 35. |
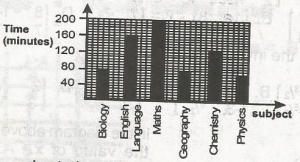 The bar chart above shows the allotment of time(in minutes) per week for selected subjects in a certain school. What is the total time allocated to the six subjects per week? A. 460mins B. 720mins C. 960mins D. 200mins Detailed Solution80 + 160 + 200 + 80 + 128 + 72 = 720minutesThere is an explanation video available below. |
|
| 36. |
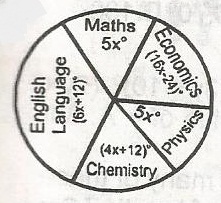 The pie chart above shows the statistical distribution of 80 students in five subjects in an examination. Calculate how many student offer Mathematics. A. 30 B. 11 C. 50 D. 20 Detailed Solution5x° + (16x - 24)° + 5x° + (4x + 12)° + (6x + 12)° = 360°36x° - 24 + 12 + 12 = 360° 36x° = 360° x° = \(\frac{360°}{36}\) = 10° Thus, the angle of sector representing Mathematics is 5 x 10° = 50°. Hence the number of students who offer mathematics is \(\frac{50}{360} \times 80 \approx 11\) There is an explanation video available below. |
|
| 37. |
If the angles of a quadrilateral are (3y + 10)°, (2y + 30)°, (y + 20)° and 4y°. Find the value of y. A. 66° B. 12° C. 30° D. 42° Detailed SolutionSum of angles in a quadrilateral = 360°\(\therefore\) (3y + 10) + (2y + 30) + (y + 20) + 4y = 360 10y + 60 = 360 \(\implies\) 10y = 300 y = 30° There is an explanation video available below. |
|
| 38. |
A square tile has side 30 cm. How many of these tiles will cover a rectangular floor of length 7.2m and width 4.2m? A. 720 B. 336 C. 420 D. 576 Detailed SolutionLength of the tile = 30 cm = 0.3mArea of the tile = 0.3 \(\times\) 0,3 = 0.09 m\(^2\) Area of the room = (7.2 \(\times\) 4.2)m\(^2\) Number of tiles = \(\frac{7.2 \times 4.2}{0.09}\) = 336 There is an explanation video available below. |
|
| 39. |
Find the length of a chord which subtends an angle of 90° at the centre of a circle whose radius is 8 cm. A. \(8\sqrt{3}\) cm B. 4 cm C. 8 cm D. \(8\sqrt{2}\) cm Detailed SolutionLength of chord = \(2r \sin (\frac{\theta}{2})\)= \(2 \times 8 \times \sin (\frac{90}{2})\) = \(16 \times \frac{\sqrt{2}}{2}\) = \(8\sqrt{2} cm\) There is an explanation video available below. |
|
| 40. |
A chord of a circle subtends an angle of 120° at the centre of a circle of diameter \(4\sqrt{3} cm\). Calculate the area of the major sector. A. 32\(\pi\) cm\(^2\) B. 4\(\pi\) cm\(^2\) C. 8\(\pi\) cm\(^2\) D. 16\(\pi\) cm\(^2\) Detailed SolutionAngle of major sector = 360° - 120° = 240°Area of major sector : \(\frac{\theta}{360} \times \pi r^{2}\) r = \(\frac{4\sqrt{3}}{2} = 2\sqrt{3} cm\) Area : \(\frac{240}{360} \times \pi \times (2\sqrt{3})^{2}\) = \(8\pi cm^{2}\) There is an explanation video available below. |
| 31. |
A basket contains 9 apples, 8 bananas and 7 oranges. A fruit is picked from the basket, find the probability that it is neither an apple nor an orange. A. \(\frac{3}{8}\) B. \(\frac{1}{3}\) C. \(\frac{7}{24}\) D. \(\frac{2}{3}\) Detailed Solutionn(apples) = 9n(bananas) = 8 n(oranges) = 7 n(\(\varepsilon\)) = 24 Hence Prob(not apple, nor orange) = Prob(banana) = \(\frac{8}{24}\) = \(\frac{1}{3}\) There is an explanation video available below. |
|
| 32. |
 The graph above is correctly represented by A. y = x2 - x - 2 B. y = x2 - 3x + 2 C. y = x2 - x - 1 D. y = x2 + x - 2 Detailed SolutionThe graph crosses the x-axis at x = -1 and x = 2Thus, x + 1 = 0 and x - 2 = 0 x\(^2\) - 2x + x - 2 = 0 x\(^2\) - x - 2 = 0 giving y = x\(^2\) - x - 2 There is an explanation video available below. |
|
| 33. |
 In the diagram given, find the value of x. A. 30o B. 40o C. 45o D. 15o |
|
| 34. |
 The value x in the figure given is A. 110o B. 100o C. 70o D. 130o Detailed Solution
180° - x + 60 + 70 = 180 130° - x = 180° - 180° = 0° x = 130° There is an explanation video available below. |
|
| 35. |
 The bar chart above shows the allotment of time(in minutes) per week for selected subjects in a certain school. What is the total time allocated to the six subjects per week? A. 460mins B. 720mins C. 960mins D. 200mins Detailed Solution80 + 160 + 200 + 80 + 128 + 72 = 720minutesThere is an explanation video available below. |
| 36. |
 The pie chart above shows the statistical distribution of 80 students in five subjects in an examination. Calculate how many student offer Mathematics. A. 30 B. 11 C. 50 D. 20 Detailed Solution5x° + (16x - 24)° + 5x° + (4x + 12)° + (6x + 12)° = 360°36x° - 24 + 12 + 12 = 360° 36x° = 360° x° = \(\frac{360°}{36}\) = 10° Thus, the angle of sector representing Mathematics is 5 x 10° = 50°. Hence the number of students who offer mathematics is \(\frac{50}{360} \times 80 \approx 11\) There is an explanation video available below. |
|
| 37. |
If the angles of a quadrilateral are (3y + 10)°, (2y + 30)°, (y + 20)° and 4y°. Find the value of y. A. 66° B. 12° C. 30° D. 42° Detailed SolutionSum of angles in a quadrilateral = 360°\(\therefore\) (3y + 10) + (2y + 30) + (y + 20) + 4y = 360 10y + 60 = 360 \(\implies\) 10y = 300 y = 30° There is an explanation video available below. |
|
| 38. |
A square tile has side 30 cm. How many of these tiles will cover a rectangular floor of length 7.2m and width 4.2m? A. 720 B. 336 C. 420 D. 576 Detailed SolutionLength of the tile = 30 cm = 0.3mArea of the tile = 0.3 \(\times\) 0,3 = 0.09 m\(^2\) Area of the room = (7.2 \(\times\) 4.2)m\(^2\) Number of tiles = \(\frac{7.2 \times 4.2}{0.09}\) = 336 There is an explanation video available below. |
|
| 39. |
Find the length of a chord which subtends an angle of 90° at the centre of a circle whose radius is 8 cm. A. \(8\sqrt{3}\) cm B. 4 cm C. 8 cm D. \(8\sqrt{2}\) cm Detailed SolutionLength of chord = \(2r \sin (\frac{\theta}{2})\)= \(2 \times 8 \times \sin (\frac{90}{2})\) = \(16 \times \frac{\sqrt{2}}{2}\) = \(8\sqrt{2} cm\) There is an explanation video available below. |
|
| 40. |
A chord of a circle subtends an angle of 120° at the centre of a circle of diameter \(4\sqrt{3} cm\). Calculate the area of the major sector. A. 32\(\pi\) cm\(^2\) B. 4\(\pi\) cm\(^2\) C. 8\(\pi\) cm\(^2\) D. 16\(\pi\) cm\(^2\) Detailed SolutionAngle of major sector = 360° - 120° = 240°Area of major sector : \(\frac{\theta}{360} \times \pi r^{2}\) r = \(\frac{4\sqrt{3}}{2} = 2\sqrt{3} cm\) Area : \(\frac{240}{360} \times \pi \times (2\sqrt{3})^{2}\) = \(8\pi cm^{2}\) There is an explanation video available below. |