Year :
2010
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
41 - 49 of 49 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
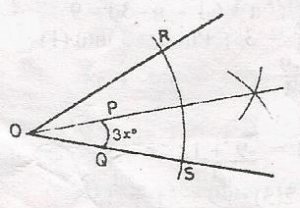 In the diagram, < ROS = 66o and < POQ = 3x. some construction lines are shown. Calculate the value of x. A. 10o B. 11o C. 22o D. 35o Detailed SolutionFrom the diagram, OP bisects < ROS< POS = \(\frac{1}{2}\) < ROS = \(\frac{1}{2}\) x 66o 3x = 33o x = \(\frac{33^o}{3}\) = 11o |
|
| 42. |
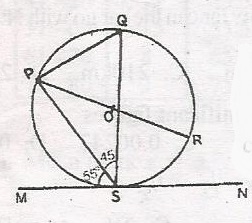 In the diagram, the tangent MN makes an angle of 55o with the chord PS. IF O is the centre of the circle, find < RPS A. 55o B. 45o C. 35o D. 25o Detailed SolutionJoin SR< PRS = 90o(Angle in a semicircle) < PRS = 55o (Angle between a chord and a tangent = Angle in the alternate segment) < PSR + < PRS + < RSP = 180o 90v + 55o + < RSp = 180o < RSP = 180o - 145o = 35o |
|
| 43. |
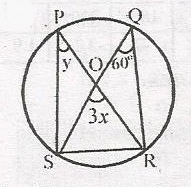 In the diagram, O is the centre of the circle, < SQR = 60o, < SPR = y and < SOR = 3x. Find the value of (x + y) A. 110o B. 100o C. 80o D. 70o Detailed Solution3x = 2 x 60 = 2y (Angle at centre = 2 x angle at circumference)3x = 2 x 60 x = \(\frac{2 \times 60}{3}\) = 40o 2 x 60 = 2y y = 60o x + y = 40 + 60 = 100o |
|
| 44. |
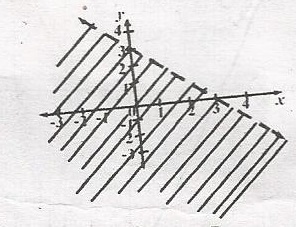 The shaded portion in the diagram is the solution of A. x + y \(\leq\) 3 B. x + y < 3 C. x + y > 3 D. x + y \(\geq\) 3 Detailed SolutionUsing \(\frac{x}{a} + \frac{y}{b}\) < 1for the equation of the timewhere a = intercept on x-axis and b = intercept on y - axis \(\frac{x}{3} + \frac{y}{3} = 1\) = \(\frac{x + y}{3} = 1\) = x + y < 3 |
|
| 45. |
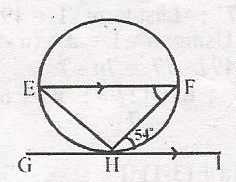 In the diagram, GI is a tangent to the circle at H. If EF//GI, calculate the size of < EHF A. 126o B. 72o C. 64cmo D. 32cmo Detailed SolutionF = 54o (Alternate triangle angles)< GHE = F = 54o(Angle between a chord and a tangent = angles in the alternate segment) Now, < GHE + < EHF + < IHF = 180o(Angles on a straight line) 54o + < EHF + 54o = 180o < EHF = 180o - 108o = 72o |
|
| 46. |
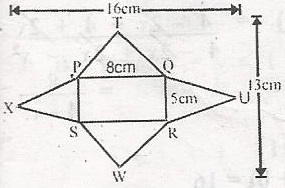 The diagram is a net right rectangular pyramid. Calculate the total surface area A. 208cm2 B. 112cm2 C. 92cm2 D. 76cm2 Detailed SolutionTotal surface area = sum of the area of the \(\bigtriangleup\) S + Area of the rectangle= 2 x Area of \(\bigtriangleup\) PTQ + 2 x Area of \(\bigtriangleup\) QUR + Area of rectangle PQRS 2 x \(\frac{1}{2}\)(8 x 4) + 2 x \(\frac{1}{2}\)(5 x 4) + 8 x 5 = 32 + 20 + 40 = 92cm2 |
|
| 47. |
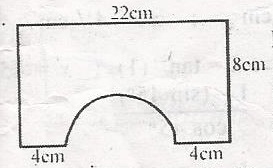 The diagram shows a rectangular cardboard from which a semi-circle is cut off. Calculate the area of the remaining part A. 44cm2 B. 99cm2 C. 154cm2 D. 165cm2 Detailed SolutionArea of remaining = Area of rectangle = Area of semi-circle22 x 8 - \(\frac{1}{2}\)xar2 ehere r - \(\frac{14}{2}\)cm = 7cm Area of remaining = 176 - \(\frac{1}{2}\) x \(\frac{22}{4}\) x 7 x 7 = 176 - 77 = 99cm2 |
|
| 48. |
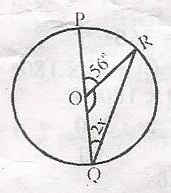 In the diagram, 0 is the centre of the circle. Find the value x A. 34 B. 29 C. 17 D. 14 Detailed SolutionPOQ in a straight lineHence, < POQ + < QOR = 180o 56o + < QOR = 180o < QOR = 180o - 56o = 124o Now, in \(\bigtriangleup\) QOR OR = OQ = Radius < ORQ = < OQR = 2x (Base angles of an Isosceles \(\bigtriangleup\)) 2x + 124 + 2x = 180o 4x + 124 = 180 4x = 180 - 124 4x = 56 x = \(\frac{56}{4}\) x = 14o |
|
| 49. |
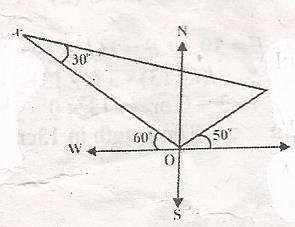 In the diagram, < WOX = 60o, < YOE = 50o and < OXY = 30o. What is the bearing of x from y? A. 300o B. 240o C. 190o D. 150o Detailed SolutionThe bearing of x from y = 270o + \(\theta\)where \(\theta\) + 50o = y in \(\bigtriangleup\) OXY O + X + Y = 180o Where O = 40o + 30o = 70o 70o + 30o + y = 180o y + 100o = 180o y = 180o - 100o = 30o \(\theta\) + 50o = 80 |
| 41. |
 In the diagram, < ROS = 66o and < POQ = 3x. some construction lines are shown. Calculate the value of x. A. 10o B. 11o C. 22o D. 35o Detailed SolutionFrom the diagram, OP bisects < ROS< POS = \(\frac{1}{2}\) < ROS = \(\frac{1}{2}\) x 66o 3x = 33o x = \(\frac{33^o}{3}\) = 11o |
|
| 42. |
 In the diagram, the tangent MN makes an angle of 55o with the chord PS. IF O is the centre of the circle, find < RPS A. 55o B. 45o C. 35o D. 25o Detailed SolutionJoin SR< PRS = 90o(Angle in a semicircle) < PRS = 55o (Angle between a chord and a tangent = Angle in the alternate segment) < PSR + < PRS + < RSP = 180o 90v + 55o + < RSp = 180o < RSP = 180o - 145o = 35o |
|
| 43. |
 In the diagram, O is the centre of the circle, < SQR = 60o, < SPR = y and < SOR = 3x. Find the value of (x + y) A. 110o B. 100o C. 80o D. 70o Detailed Solution3x = 2 x 60 = 2y (Angle at centre = 2 x angle at circumference)3x = 2 x 60 x = \(\frac{2 \times 60}{3}\) = 40o 2 x 60 = 2y y = 60o x + y = 40 + 60 = 100o |
|
| 44. |
 The shaded portion in the diagram is the solution of A. x + y \(\leq\) 3 B. x + y < 3 C. x + y > 3 D. x + y \(\geq\) 3 Detailed SolutionUsing \(\frac{x}{a} + \frac{y}{b}\) < 1for the equation of the timewhere a = intercept on x-axis and b = intercept on y - axis \(\frac{x}{3} + \frac{y}{3} = 1\) = \(\frac{x + y}{3} = 1\) = x + y < 3 |
|
| 45. |
 In the diagram, GI is a tangent to the circle at H. If EF//GI, calculate the size of < EHF A. 126o B. 72o C. 64cmo D. 32cmo Detailed SolutionF = 54o (Alternate triangle angles)< GHE = F = 54o(Angle between a chord and a tangent = angles in the alternate segment) Now, < GHE + < EHF + < IHF = 180o(Angles on a straight line) 54o + < EHF + 54o = 180o < EHF = 180o - 108o = 72o |
| 46. |
 The diagram is a net right rectangular pyramid. Calculate the total surface area A. 208cm2 B. 112cm2 C. 92cm2 D. 76cm2 Detailed SolutionTotal surface area = sum of the area of the \(\bigtriangleup\) S + Area of the rectangle= 2 x Area of \(\bigtriangleup\) PTQ + 2 x Area of \(\bigtriangleup\) QUR + Area of rectangle PQRS 2 x \(\frac{1}{2}\)(8 x 4) + 2 x \(\frac{1}{2}\)(5 x 4) + 8 x 5 = 32 + 20 + 40 = 92cm2 |
|
| 47. |
 The diagram shows a rectangular cardboard from which a semi-circle is cut off. Calculate the area of the remaining part A. 44cm2 B. 99cm2 C. 154cm2 D. 165cm2 Detailed SolutionArea of remaining = Area of rectangle = Area of semi-circle22 x 8 - \(\frac{1}{2}\)xar2 ehere r - \(\frac{14}{2}\)cm = 7cm Area of remaining = 176 - \(\frac{1}{2}\) x \(\frac{22}{4}\) x 7 x 7 = 176 - 77 = 99cm2 |
|
| 48. |
 In the diagram, 0 is the centre of the circle. Find the value x A. 34 B. 29 C. 17 D. 14 Detailed SolutionPOQ in a straight lineHence, < POQ + < QOR = 180o 56o + < QOR = 180o < QOR = 180o - 56o = 124o Now, in \(\bigtriangleup\) QOR OR = OQ = Radius < ORQ = < OQR = 2x (Base angles of an Isosceles \(\bigtriangleup\)) 2x + 124 + 2x = 180o 4x + 124 = 180 4x = 180 - 124 4x = 56 x = \(\frac{56}{4}\) x = 14o |
|
| 49. |
 In the diagram, < WOX = 60o, < YOE = 50o and < OXY = 30o. What is the bearing of x from y? A. 300o B. 240o C. 190o D. 150o Detailed SolutionThe bearing of x from y = 270o + \(\theta\)where \(\theta\) + 50o = y in \(\bigtriangleup\) OXY O + X + Y = 180o Where O = 40o + 30o = 70o 70o + 30o + y = 180o y + 100o = 180o y = 180o - 100o = 30o \(\theta\) + 50o = 80 |