Mathematics (Core), 2013, WASSCE/WAEC MAY/JUNE, Exam, Paper 1 | Objectives

Paper Info

Year :

2013

Title :

Mathematics (Core)

Exam :

WASSCE/WAEC MAY/JUNE

Paper 1 | Objectives

31 - 40 of 48 Questions

#	Question	Ans
31.	The slant height of a cone is 5cm and the radius of its base is 3cm. Find, correct to the nearest whole number, the volume of the cone. ( Take \(\pi = \frac{22}{7}\)) A. 48cm³ B. 47cm³ C. 38cm³ D. 12cm³ Show Content Detailed Solution Volume of a cone = \(\frac{1}{3} \pi r^2h\) h² = 5² = 3² = 25 - 9 = 16 h = \(\sqrt{16}\) h = 4cm v = \(\frac{1}{3} \times \frac{22}{7} \times 3^2 \times 4\) \(\frac{1}{3} \times \frac{22}{7} \times 9 \times 4\) = \(\frac{22 \times 3 \times 4}{7}\) = 37.7cm³ = 38cm³	C
32.	The distance between two towns is 50km. It is represented on a map by 5cm. Find the scale used A. 1: 1,000,000 B. 1: 500,000 C. 1: 100,000 D. 1: 10,000 Show Content Detailed Solution 1km = 100,000cm on the map 1 cm represent every 10 km which is equal to (10 x 100,000cm) = 1,000,000cm the scale is 1:1,000,000	A
33.	Given that (x + 2)(x² - 3x + 2) + 2(x + 2)(x - 1) = (x + 2) M, find M A. (x + 2)² B. x(x + 2) C. xv + 2 D. x² - x Show Content Detailed Solution (x = 2)(x² - 3x + 2) + 2(x + 2)(x - 1) = (x + 2)m (m + 2)[(x² - 3x + 2) + 2(x - 1)] = (x + 2)M divide both side by (x + 2) (x² - 3x + 2) + 2(x - 1) = M x² - 3x + 2 + 2x - 2 = M x² - 3x + 2 + 2x - 2 = M x² - 3x + 2x = M x² - x = M M = x² - x	D
34.	An open cone with base radius 28cm and perpendicular height 96cm was stretched to form sector of a circle. calculate the arc of the sector (Take \(\pi = \frac{22}{7}\)) A. 8800cm² B. 8448cm² C. 4400cm² D. 4224cm² Show Content Detailed Solution L² = 96² + 28² = 9216 + 784 = 10000 L = \(\sqrt{10000}\) = 100cm curved surface area = \(\pi r l\) = \(\frac{22}{7} \times 28 \times 100\) = 8800cm² area of cone = area of sector area of sector = 8800cm²	A
35.	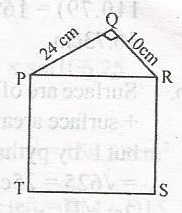In the diagram, PRST is a square. If \|PQ\| = 24cm. \|QR\| = 10cm and < PQR = 90^o, find the perimeter of the polygon PQRST. A. 112cm B. 98cm C. 86cm D. 84cm	A
36.	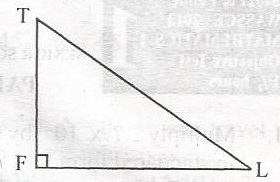In the diagram, the height of a flagpole \|TF\| and the length of its shadow \|FL\| re in the ratio 6:8. Using k as a constant of proportionality, find the shortest distance between T and L A. 7K units B. 10K units C. 12K units D. 14k units Show Content Detailed Solution by Pythagoras x² = 6² + 8² 36 + 64 = 100 x = \(\sqrt{100}\) x = 10	B
37.	In the diagrams, \|XZ\| = \|MN\|, \|ZY\| = \|MO\| and \|XY\| = \|NO\|. Which of the following statements is true? A. \(\bigtriangleup\) ZYX = \(\bigtriangleup\) OMN B. \(\bigtriangleup\) YZX = \(\bigtriangleup\) NOM C. \(\bigtriangleup\) ZXY= \(\bigtriangleup\) MON D. \(\bigtriangleup\) XYZ= \(\bigtriangleup\) NOM	D
38.	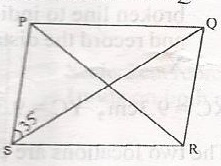In the diagram, PQRS is a rhombus and < PSQ = 35^o. Calculate the size of < PRO A. 65^o B. 55^o C. 45^o D. 35^o Show Content Detailed Solution The diagonals of rhombus bisects its angles	D
39.	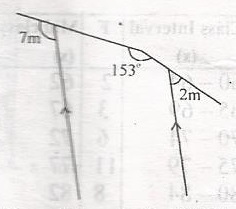Find the value of m in the diagram A. 34^o B. 27^o C. 23^o D. 17^o Show Content Detailed Solution \(\bigtriangleup\) ABC, A + 153 = 180 (angles on straight line) < A = 180 - 153 = 27 < B = 2m(vertically opposite angles) < C = 7m (corresponding ngles) < A + < B + < C = 180 (sum of int. angles of \(\bigtriangleup\)) i.e. 27 + 2m + 7m = 180^o 9m = 180 - 27 9m = 153 m = \(\frac{153}{9}\) = 17	D
40.	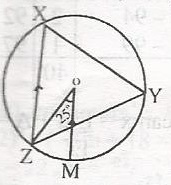In the diagram, O is the centre of the circle. OM\|\|XZ and < ZOM = 25^o A. 50^o B. 55^o C. 60^o D. 65^o	C

31.	The slant height of a cone is 5cm and the radius of its base is 3cm. Find, correct to the nearest whole number, the volume of the cone. ( Take \(\pi = \frac{22}{7}\)) A. 48cm³ B. 47cm³ C. 38cm³ D. 12cm³ Show Content Detailed Solution Volume of a cone = \(\frac{1}{3} \pi r^2h\) h² = 5² = 3² = 25 - 9 = 16 h = \(\sqrt{16}\) h = 4cm v = \(\frac{1}{3} \times \frac{22}{7} \times 3^2 \times 4\) \(\frac{1}{3} \times \frac{22}{7} \times 9 \times 4\) = \(\frac{22 \times 3 \times 4}{7}\) = 37.7cm³ = 38cm³	C
32.	The distance between two towns is 50km. It is represented on a map by 5cm. Find the scale used A. 1: 1,000,000 B. 1: 500,000 C. 1: 100,000 D. 1: 10,000 Show Content Detailed Solution 1km = 100,000cm on the map 1 cm represent every 10 km which is equal to (10 x 100,000cm) = 1,000,000cm the scale is 1:1,000,000	A
33.	Given that (x + 2)(x² - 3x + 2) + 2(x + 2)(x - 1) = (x + 2) M, find M A. (x + 2)² B. x(x + 2) C. xv + 2 D. x² - x Show Content Detailed Solution (x = 2)(x² - 3x + 2) + 2(x + 2)(x - 1) = (x + 2)m (m + 2)[(x² - 3x + 2) + 2(x - 1)] = (x + 2)M divide both side by (x + 2) (x² - 3x + 2) + 2(x - 1) = M x² - 3x + 2 + 2x - 2 = M x² - 3x + 2 + 2x - 2 = M x² - 3x + 2x = M x² - x = M M = x² - x	D
34.	An open cone with base radius 28cm and perpendicular height 96cm was stretched to form sector of a circle. calculate the arc of the sector (Take \(\pi = \frac{22}{7}\)) A. 8800cm² B. 8448cm² C. 4400cm² D. 4224cm² Show Content Detailed Solution L² = 96² + 28² = 9216 + 784 = 10000 L = \(\sqrt{10000}\) = 100cm curved surface area = \(\pi r l\) = \(\frac{22}{7} \times 28 \times 100\) = 8800cm² area of cone = area of sector area of sector = 8800cm²	A
35.	In the diagram, PRST is a square. If \|PQ\| = 24cm. \|QR\| = 10cm and < PQR = 90^o, find the perimeter of the polygon PQRST. A. 112cm B. 98cm C. 86cm D. 84cm	A

36.	In the diagram, the height of a flagpole \|TF\| and the length of its shadow \|FL\| re in the ratio 6:8. Using k as a constant of proportionality, find the shortest distance between T and L A. 7K units B. 10K units C. 12K units D. 14k units Show Content Detailed Solution by Pythagoras x² = 6² + 8² 36 + 64 = 100 x = \(\sqrt{100}\) x = 10	B
37.	In the diagrams, \|XZ\| = \|MN\|, \|ZY\| = \|MO\| and \|XY\| = \|NO\|. Which of the following statements is true? A. \(\bigtriangleup\) ZYX = \(\bigtriangleup\) OMN B. \(\bigtriangleup\) YZX = \(\bigtriangleup\) NOM C. \(\bigtriangleup\) ZXY= \(\bigtriangleup\) MON D. \(\bigtriangleup\) XYZ= \(\bigtriangleup\) NOM	D
38.	In the diagram, PQRS is a rhombus and < PSQ = 35^o. Calculate the size of < PRO A. 65^o B. 55^o C. 45^o D. 35^o Show Content Detailed Solution The diagonals of rhombus bisects its angles	D
39.	Find the value of m in the diagram A. 34^o B. 27^o C. 23^o D. 17^o Show Content Detailed Solution \(\bigtriangleup\) ABC, A + 153 = 180 (angles on straight line) < A = 180 - 153 = 27 < B = 2m(vertically opposite angles) < C = 7m (corresponding ngles) < A + < B + < C = 180 (sum of int. angles of \(\bigtriangleup\)) i.e. 27 + 2m + 7m = 180^o 9m = 180 - 27 9m = 153 m = \(\frac{153}{9}\) = 17	D
40.	In the diagram, O is the centre of the circle. OM\|\|XZ and < ZOM = 25^o A. 50^o B. 55^o C. 60^o D. 65^o	C