Year :
2002
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
41 - 49 of 49 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
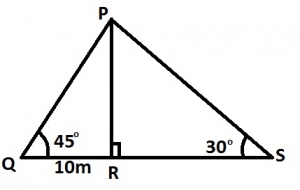 In the diagram, |QR| = 10cm, PR⊥QS, angle PSR = 30° and angle PQR = 45°. Calculate in meters |QS| A. \(10(1+\sqrt{3})\) B. \(20\sqrt{3}\) C. \(10\sqrt{3}\) D. \((10+\sqrt{3})\) Detailed SolutionIn \(\Delta\) PQR,\(\tan 45 = \frac{PR}{10} \implies PR = 10 \tan 45\) = 10m In \(\Delta\) PRS, \(\tan 30 = \frac{10}{RS} \implies RS = \frac{10}{\tan 30}\) = \(\frac{10}{\frac{1}{\sqrt{3}}\) = \(10\sqrt{3}\) PS = \(10 + 10\sqrt{3}\) = \(10(1 + \sqrt{3}) cm\) |
|
| 42. |
Calculate and correct to two significant figures, the percentage error in approximating 0.375 to 0.4 A. 2.0 B. 2.5 C. 6.6 D. 6.7 Detailed SolutionMeasured value = 0.375Approximation = 0.4 Error = 0.4 - 0.375 = 0.025 Error% = \(\frac{0.025}{0.375}\) x 100% = 6.67% = 6.7% |
|
| 43. |
To arrive on schedule, a train is to cover a distance of 60km at 72km/hr. If it starts 10 minutes late, at what speed must it move to arrive on schedule? A. 60km/hr B. 80km/hr C. 90km/hr D. 108km/hr Detailed Solution\(speed = \frac{distance}{time}\\72 = \frac{60}{time}\\ t = \frac{60}{72} = \frac{5}{6}hr\) time lost = 10mis \(= \frac{10}{60}hr = \frac{1}{6}\) Time required for the journey \(=\frac{5}{6}-\frac{1}{6} = \frac{2}{3}\\ speed \hspace{1mm}=60 \div \frac{2}{3} = 90km/hr\) |
|
| 44. |
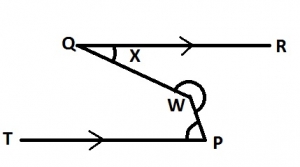 In the diagram, \(QR||TP and W\hat{P}T = 88^{\circ} \). Find the value of x A. 92o B. 68o C. 67o D. 23o Detailed Solution Sum of the angles in a triangle = 180° 3x - 180° + 92° + x = 180° 4x - 88° = 180° 4x = 268° x = 67° |
|
| 45. |
 In the diagram O is the center of the circle, ∠SOR = 64° and ∠PSO = 36°. Calculate ∠PQR A. 100o B. 96o C. 94o D. 86o Detailed Solution< OSR = < ORS = \(\frac{180° - 64°}{2}\) = 58°< PSR = 36° + 58° = 94° < PSR + < PQR = 180° 94° + < PQR = 180° \(\implies\) < PQR = 180° - 94° = 86° |
|
| 46. |
Given that \(p = x-\frac{1}{x} and\hspace{1mm}q = x^2 + \frac{1}{x^2}\) express q in terms of p. A. (p2 + 2) B. (p - 2) 2 C. (p + 2) 2 D. (p2 - 2) Detailed SolutionGiven \(p = x - \frac{1}{x}\); \(q = x^2 + \frac{1}{x^2}\).\(p^2 = (x - \frac{1}{x})(x - \frac{1}{x})\) \(p^2 = x^2 + \frac{1}{x^2} - 2\) \(p^2 = q - 2 \implies q = p^2 + 2\) |
|
| 47. |
The number of goals scored by a school team in 10 netball matches are as follows: 3, 5, 7, 7, 8, 8, 8, 11, 11, 12. Find the probability that in a match, the school team will score at most 8 goals. A. \(\frac{7}{10}\) B. \(\frac{2}{5}\) C. \(\frac{3}{5}\) D. \(\frac{1}{5}\) Detailed SolutionNumber of at most 8 goals = 7P(at most 8 goals) = \(\frac{7}{10}\) |
|
| 48. |
Which of the following is not a rational number? A. -5 B. \(\sqrt{4}\) C. \(3\frac{3}{4}\) D. \(\sqrt{90}\) |
D |
| 49. |
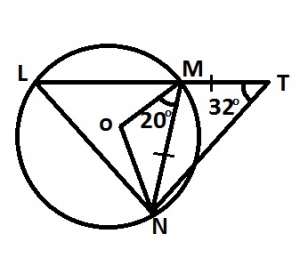 In the diagram, LMT is a straight line. lf O is the centre of circle LMN, OMN = 20°, LTN = 32° and |NM| = |MT|, find LNM. A. 44o B. 46o C. 52o D. 70o Detailed Solution< MNT = < MTN = 32°< NMT = 180° - 2(32°) = 116° < OMN + < NMT + < LMO = 180° 20° + 116° + < LMO = 180° \(\implies\) < LMO = 180° - 136° = 44° < LMN = < LMO + < OMN = 44° + 20° = 64° < NOM = 180° - 2(20°) = 140° < NLM = \(\frac{1}{2} \times < NOM = 70°\) < LNM + < LMN + < NLM = 180° < LNM + 64° + 70° = 180° < LNM = 180° - 134° = 46&a |
| 41. |
 In the diagram, |QR| = 10cm, PR⊥QS, angle PSR = 30° and angle PQR = 45°. Calculate in meters |QS| A. \(10(1+\sqrt{3})\) B. \(20\sqrt{3}\) C. \(10\sqrt{3}\) D. \((10+\sqrt{3})\) Detailed SolutionIn \(\Delta\) PQR,\(\tan 45 = \frac{PR}{10} \implies PR = 10 \tan 45\) = 10m In \(\Delta\) PRS, \(\tan 30 = \frac{10}{RS} \implies RS = \frac{10}{\tan 30}\) = \(\frac{10}{\frac{1}{\sqrt{3}}\) = \(10\sqrt{3}\) PS = \(10 + 10\sqrt{3}\) = \(10(1 + \sqrt{3}) cm\) |
|
| 42. |
Calculate and correct to two significant figures, the percentage error in approximating 0.375 to 0.4 A. 2.0 B. 2.5 C. 6.6 D. 6.7 Detailed SolutionMeasured value = 0.375Approximation = 0.4 Error = 0.4 - 0.375 = 0.025 Error% = \(\frac{0.025}{0.375}\) x 100% = 6.67% = 6.7% |
|
| 43. |
To arrive on schedule, a train is to cover a distance of 60km at 72km/hr. If it starts 10 minutes late, at what speed must it move to arrive on schedule? A. 60km/hr B. 80km/hr C. 90km/hr D. 108km/hr Detailed Solution\(speed = \frac{distance}{time}\\72 = \frac{60}{time}\\ t = \frac{60}{72} = \frac{5}{6}hr\) time lost = 10mis \(= \frac{10}{60}hr = \frac{1}{6}\) Time required for the journey \(=\frac{5}{6}-\frac{1}{6} = \frac{2}{3}\\ speed \hspace{1mm}=60 \div \frac{2}{3} = 90km/hr\) |
|
| 44. |
 In the diagram, \(QR||TP and W\hat{P}T = 88^{\circ} \). Find the value of x A. 92o B. 68o C. 67o D. 23o Detailed Solution Sum of the angles in a triangle = 180° 3x - 180° + 92° + x = 180° 4x - 88° = 180° 4x = 268° x = 67° |
|
| 45. |
 In the diagram O is the center of the circle, ∠SOR = 64° and ∠PSO = 36°. Calculate ∠PQR A. 100o B. 96o C. 94o D. 86o Detailed Solution< OSR = < ORS = \(\frac{180° - 64°}{2}\) = 58°< PSR = 36° + 58° = 94° < PSR + < PQR = 180° 94° + < PQR = 180° \(\implies\) < PQR = 180° - 94° = 86° |
| 46. |
Given that \(p = x-\frac{1}{x} and\hspace{1mm}q = x^2 + \frac{1}{x^2}\) express q in terms of p. A. (p2 + 2) B. (p - 2) 2 C. (p + 2) 2 D. (p2 - 2) Detailed SolutionGiven \(p = x - \frac{1}{x}\); \(q = x^2 + \frac{1}{x^2}\).\(p^2 = (x - \frac{1}{x})(x - \frac{1}{x})\) \(p^2 = x^2 + \frac{1}{x^2} - 2\) \(p^2 = q - 2 \implies q = p^2 + 2\) |
|
| 47. |
The number of goals scored by a school team in 10 netball matches are as follows: 3, 5, 7, 7, 8, 8, 8, 11, 11, 12. Find the probability that in a match, the school team will score at most 8 goals. A. \(\frac{7}{10}\) B. \(\frac{2}{5}\) C. \(\frac{3}{5}\) D. \(\frac{1}{5}\) Detailed SolutionNumber of at most 8 goals = 7P(at most 8 goals) = \(\frac{7}{10}\) |
|
| 48. |
Which of the following is not a rational number? A. -5 B. \(\sqrt{4}\) C. \(3\frac{3}{4}\) D. \(\sqrt{90}\) |
D |
| 49. |
 In the diagram, LMT is a straight line. lf O is the centre of circle LMN, OMN = 20°, LTN = 32° and |NM| = |MT|, find LNM. A. 44o B. 46o C. 52o D. 70o Detailed Solution< MNT = < MTN = 32°< NMT = 180° - 2(32°) = 116° < OMN + < NMT + < LMO = 180° 20° + 116° + < LMO = 180° \(\implies\) < LMO = 180° - 136° = 44° < LMN = < LMO + < OMN = 44° + 20° = 64° < NOM = 180° - 2(20°) = 140° < NLM = \(\frac{1}{2} \times < NOM = 70°\) < LNM + < LMN + < NLM = 180° < LNM + 64° + 70° = 180° < LNM = 180° - 134° = 46&a |