Year :
2011
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
31 - 40 of 49 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
John pours 96 litres of red oil into a rectangular container with length 220cm and breadth 40cm. Calculate, correct to the nearest cm, the height of the oil in the container A. 11cm B. 18cm C. 21cm D. 34cm Detailed Solutionvolume of rectangular container = L x B x H1 litre = 1000cm3 96 litres = \(\frac{1000cm^3}{1 litres}\) x 96 litres volume = 96000cm3 96000 = 220 x 40 x 11 96--- = 8800H H = \(\frac{96000}{8800}\) = 10.97cm = 11cm |
|
| 32. |
John pours 96 litres of red oil into a rectangular container with length 220cm and breadth 40cm. Calculate, correct to the nearest cm, the height of the oil in the container A. 11cm B. 18cm C. 21cm D. 34cm Detailed Solutionvolume of rectangular container = L x B x H1 litre = 1000cm3 96 litres = \(\frac{1000cm^3}{1 litres}\) x 96 litres volume = 96000cm3 96000 = 220 x 40 x 11 96--- = 8800H H = \(\frac{96000}{8800}\) = 10.97cm = 11cm |
|
| 33. |
In a quiz competition, a student answers n questions correctly and was given D(n + 50) for each question correctly answered. If he gets D600.00 altogether, how many questions did he answer correctly? A. 18 B. 15 C. 12 D. 10 Detailed Solutionlet the number of question = nn(n + 50) = 600 n2 + 50n - 600 - 0 by quadratic formular x = \(\frac{b \pm \sqrt{b^2 - 4ac}}{2}\) n = \(\frac{-50 \pm \sqrt{50^2 - 4(1) (-600)}}{2(1)}\) = \(\frac{-50 \pm \sqrt{4900}}{2}\) = \(\frac{-50 + 70}{2}\) = \(\frac{20}{2}\) = 10 |
|
| 34. |
If 27x = 9y. Find the value of \(\frac{x}{y}\) A. \(\frac{1}{3}\) B. \(\frac{2}{3}\) C. 1\(\frac{1}{2}\) D. 3 Detailed Solution27x = 9y33x = 32y 3x = 2y |
|
| 35. |
A boy looks through a window of a building and sees a mango fruit on the ground 50m away from the foot of the building. If the window is 9m from the ground, calculate, correct to the nearest degree, the angle of depression of the mango from the window A. 9o B. 10o C. 11o D. 12o Detailed Solutiontan \(\theta\) = \(\frac{9}{50}\) = 0.18\(\theta = tan^{-1} 0.18\) \(\theta\) = 10.20 |
|
| 36. |
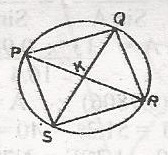 The diagram shows a cyclic quadrilateral PQRS with its diagonals intersecting at K. Which of the following triangles is similar to triangle QKR? A. \(\bigtriangleup\) PQK B. \(\bigtriangleup\) PKS C. \(\bigtriangleup\) SKR D. \(\bigtriangleup\) PSR |
C |
| 37. |
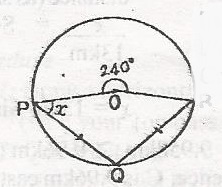 In the diagram, PO and OR are radii, |PQ| = |QR| and reflex < PQR is 240o. Calculate the value x A. 60o B. 55o C. 50o D. 45o Detailed Solution< Q = \(\frac{240}{2}\) (angle at centre twice that at the circumference)< Q = 120o Also < POR = 360 - 240 = 120o ( < s at centre) since /PQ/ = /QR/, < x = < R Byt < x + < R + O + Q = 360 (sum of interior < s of quadrilateral) x + R + 120 = 360o x + R = 360 - 240 = 120; Since x = R x + x = 120 2x = 120 Since x = R x + x = 120 2x = 120 x = \(\frac{120}{2}\) < |
|
| 38. |
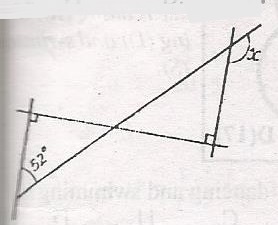 Find the size of the angle marked x in the diagram. A. 108o B. 112o C. 128o D. 142o Detailed Solutionx + 52o = 90x = 90 - 52 x = 38o k = opposite angle Z k = 38o y + k = 90o y + 38o = 90o y = 90o - 38o y = 52o y = x = 180o(sum of angles on straight line) 52 + x = 180o x = 180 - 52 x = 128 |
|
| 39. |
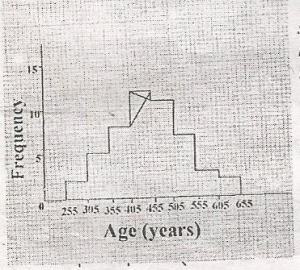 The histogram shows the age distribution of members of a club. How many members are in the club? A. 52 B. 50 C. 48 D. 40 Detailed Solution2 + 2 + 5 + 8 + 12 + H + 7 + 3 + 2 = 52 |
|
| 40. |
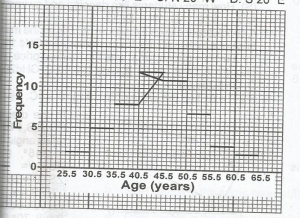 The histogram shows the age distribution of members of a club. What is their modal age? A. 44.5 B. 42.5 C. 41.5 D. 40.5 |
A |
| 31. |
John pours 96 litres of red oil into a rectangular container with length 220cm and breadth 40cm. Calculate, correct to the nearest cm, the height of the oil in the container A. 11cm B. 18cm C. 21cm D. 34cm Detailed Solutionvolume of rectangular container = L x B x H1 litre = 1000cm3 96 litres = \(\frac{1000cm^3}{1 litres}\) x 96 litres volume = 96000cm3 96000 = 220 x 40 x 11 96--- = 8800H H = \(\frac{96000}{8800}\) = 10.97cm = 11cm |
|
| 32. |
John pours 96 litres of red oil into a rectangular container with length 220cm and breadth 40cm. Calculate, correct to the nearest cm, the height of the oil in the container A. 11cm B. 18cm C. 21cm D. 34cm Detailed Solutionvolume of rectangular container = L x B x H1 litre = 1000cm3 96 litres = \(\frac{1000cm^3}{1 litres}\) x 96 litres volume = 96000cm3 96000 = 220 x 40 x 11 96--- = 8800H H = \(\frac{96000}{8800}\) = 10.97cm = 11cm |
|
| 33. |
In a quiz competition, a student answers n questions correctly and was given D(n + 50) for each question correctly answered. If he gets D600.00 altogether, how many questions did he answer correctly? A. 18 B. 15 C. 12 D. 10 Detailed Solutionlet the number of question = nn(n + 50) = 600 n2 + 50n - 600 - 0 by quadratic formular x = \(\frac{b \pm \sqrt{b^2 - 4ac}}{2}\) n = \(\frac{-50 \pm \sqrt{50^2 - 4(1) (-600)}}{2(1)}\) = \(\frac{-50 \pm \sqrt{4900}}{2}\) = \(\frac{-50 + 70}{2}\) = \(\frac{20}{2}\) = 10 |
|
| 34. |
If 27x = 9y. Find the value of \(\frac{x}{y}\) A. \(\frac{1}{3}\) B. \(\frac{2}{3}\) C. 1\(\frac{1}{2}\) D. 3 Detailed Solution27x = 9y33x = 32y 3x = 2y |
|
| 35. |
A boy looks through a window of a building and sees a mango fruit on the ground 50m away from the foot of the building. If the window is 9m from the ground, calculate, correct to the nearest degree, the angle of depression of the mango from the window A. 9o B. 10o C. 11o D. 12o Detailed Solutiontan \(\theta\) = \(\frac{9}{50}\) = 0.18\(\theta = tan^{-1} 0.18\) \(\theta\) = 10.20 |
| 36. |
 The diagram shows a cyclic quadrilateral PQRS with its diagonals intersecting at K. Which of the following triangles is similar to triangle QKR? A. \(\bigtriangleup\) PQK B. \(\bigtriangleup\) PKS C. \(\bigtriangleup\) SKR D. \(\bigtriangleup\) PSR |
C |
| 37. |
 In the diagram, PO and OR are radii, |PQ| = |QR| and reflex < PQR is 240o. Calculate the value x A. 60o B. 55o C. 50o D. 45o Detailed Solution< Q = \(\frac{240}{2}\) (angle at centre twice that at the circumference)< Q = 120o Also < POR = 360 - 240 = 120o ( < s at centre) since /PQ/ = /QR/, < x = < R Byt < x + < R + O + Q = 360 (sum of interior < s of quadrilateral) x + R + 120 = 360o x + R = 360 - 240 = 120; Since x = R x + x = 120 2x = 120 Since x = R x + x = 120 2x = 120 x = \(\frac{120}{2}\) < |
|
| 38. |
 Find the size of the angle marked x in the diagram. A. 108o B. 112o C. 128o D. 142o Detailed Solutionx + 52o = 90x = 90 - 52 x = 38o k = opposite angle Z k = 38o y + k = 90o y + 38o = 90o y = 90o - 38o y = 52o y = x = 180o(sum of angles on straight line) 52 + x = 180o x = 180 - 52 x = 128 |
|
| 39. |
 The histogram shows the age distribution of members of a club. How many members are in the club? A. 52 B. 50 C. 48 D. 40 Detailed Solution2 + 2 + 5 + 8 + 12 + H + 7 + 3 + 2 = 52 |
|
| 40. |
 The histogram shows the age distribution of members of a club. What is their modal age? A. 44.5 B. 42.5 C. 41.5 D. 40.5 |
A |