Year :
2011
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
21 - 30 of 49 Questions
| # | Question | Ans |
|---|---|---|
| 21. |
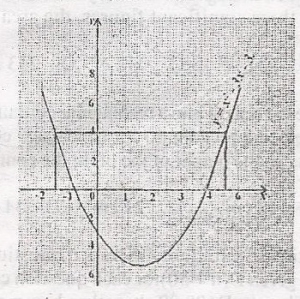 The graph represents the relation y = xo2 - 3x - 3. Find the value of x for which x2 - 3x = 7 A. -1.55, 4.44 B. 1.55, -4.55 C. -1.55, -4.55 D. 1.55, 4.55 Detailed Solutionx2 - 3x = 7x2 - 3x - 7 = 0 What can you add to both sides of the equation to give the same value of y = x2 - 3x - 3 The number is 4 x2 - 3x - 7 + 4 = 4 x2 - 3x - 3 = 4 but y = x2 - 3x - 3 y = 4; So are y = 4 draw a line parallel to x axis, to cut or intersect the graph. At these points look down to see the corresponding values on x axis This give -1.55 and 4.55 |
|
| 22. |
Simplify \(\frac{m}{n} + \frac{(m - 1)}{5n} = \frac{(m - 2)}{10n}\) where n \(\neq\) 0 A. \(\frac{m - 3}{10n}\) B. \(\frac{11m}{10n}\) C. \(\frac{m + 1}{10n}\) D. \(\frac{11m + 4}{10n}\) Detailed Solution\(\frac{m}{n} + \frac{(m - 1)}{5n} - \frac{(m - 2)}{10n}\); \(\frac{10m + 2(m - 1) - 1(m - 2)}{10m}\)= \(\frac{10m + 2m - 2 - m + 2}{10n}\) = \(\frac{10m + 2m - m - 2 + 2}{10n}\) = \(\frac{11m}{10n}\) |
|
| 23. |
If \(\sqrt{72} + \sqrt{32} - 3 \sqrt{18} = x \sqrt{8}\), Find the value of x A. 1 B. \(\frac{3}{4}\) C. \(\frac{1}{2}\) D. \(\frac{1}{4}\) Detailed Solution\(\sqrt{2} + \sqrt{32} - 3\sqrt{18} = x\sqrt{8}\)= \(\sqrt{36 \times 2} + \sqrt{16 \times 2} - 3\sqrt{2 \times 9}\) = x\(\sqrt{2 \times 4}\) = 6\(\sqrt{2} + 4\sqrt{2} - 9\sqrt{2} = 2 \times \sqrt{2}\) \(\sqrt{2} (6 + 4 - 9) = 2x\sqrt{2}\) \(\sqrt{2} = 2x \sqrt{2}\) divide both sides by \(\sqrt{2}\) \(\frac{\sqrt{2}}{\sqrt{2}} = \frac{2 \times \sqrt{2}}{\sqrt{2}}\) 1 = 2x 2x = 1 x = \(\frac{1}{2}\) |
|
| 24. |
G varies directly as the square of H, If G is 4 when H is 3, find H when G = 100 A. 15 B. 25 C. 75 D. 225 Detailed SolutionG \(\alpha\) H2G = KH2 4 = K(3)2 4 = 9k; K = \(\frac{4}{9}\) 100 = \(\frac{4}{9}H^2\) 4H2 = 900 H2 = \(\frac{900}{4}\) H2 = 225 H = \(\sqrt{225}\) H = 15 |
|
| 25. |
Given that n(p) = 19, m(P \(\cup\) Q) = 38 and n(P \(\cap\) Q) = 7, Find n(C) A. 26 B. 31 C. 36 D. 50 Detailed Solutionn(P \(\cup\) Q) = m(P \(\cap\) C)38 = 19 = n(C) - 7 n(C) = 38 - 12 = 26 |
|
| 26. |
What must be added to (2x - 3y) to get (x - 2y)? A. 5y - x B. y - x C. x - 5x D. x - y Detailed SolutionWhat must be added to 2x - 3y = Difference between x - 2y and 2x - 3yx - 2y - 2y - (2x - 3y); x - 2y - 2x + 3y = x - 2x + 3y - 2y = y - x |
|
| 27. |
Simplify 1\(\frac{3}{4} - (2 \frac{1}{3} + 4)\) A. 3\(\frac{5}{12}\) B. 2\(\frac{7}{12}\) C. -4 \(\frac{7}{12}\) D. -5 \(\frac{7}{12}\) Detailed Solution1\(\frac{3}{4} - (2 \frac{1}{3} + 4)\) = \(\frac{7}{4} - (\frac{7}{3} + \frac{4}{1})\); \(\frac{7 + 12}{3}\)\(\frac{7}{4} - \frac{19}{3} = \frac{21 + 76}{12}\) = \(\frac{-55}{12} = -4 \frac{7}{12}\) |
|
| 28. |
Find the smaller value of x that satisfies the equation x2 + 7x + 10 = 0 A. -5 B. -2 C. 2 D. 5 Detailed Solutionx2 + 7x + 10 = 0x2 + 5x + 2x + 10 = 0 x(x + 5) + 2(x + 5) = 0 (x + 2)(x + 5) = 0 x + 2 = 0 or x + 5 = 0 x = -2 or x = -5 the smaller value x = -5 |
|
| 29. |
The perpendicular bisectors of the sides of an acute-angled triangle are drawn. Which of these statements is correct? They intersect A. on one of the vertices B. at a midpoint of a side C. inside the triangle D. outside the triangle |
C |
| 30. |
A rectangular garden measures 18.6m by 12.5m. Calculate, correct to three significant figures, the area of the garden A. 230m2 B. 231m2 C. 232m2 D. 233m2 Detailed SolutionA = L x B= (18.6 x 12.5)m2 = 232.5m2 = 233m2 |
| 21. |
 The graph represents the relation y = xo2 - 3x - 3. Find the value of x for which x2 - 3x = 7 A. -1.55, 4.44 B. 1.55, -4.55 C. -1.55, -4.55 D. 1.55, 4.55 Detailed Solutionx2 - 3x = 7x2 - 3x - 7 = 0 What can you add to both sides of the equation to give the same value of y = x2 - 3x - 3 The number is 4 x2 - 3x - 7 + 4 = 4 x2 - 3x - 3 = 4 but y = x2 - 3x - 3 y = 4; So are y = 4 draw a line parallel to x axis, to cut or intersect the graph. At these points look down to see the corresponding values on x axis This give -1.55 and 4.55 |
|
| 22. |
Simplify \(\frac{m}{n} + \frac{(m - 1)}{5n} = \frac{(m - 2)}{10n}\) where n \(\neq\) 0 A. \(\frac{m - 3}{10n}\) B. \(\frac{11m}{10n}\) C. \(\frac{m + 1}{10n}\) D. \(\frac{11m + 4}{10n}\) Detailed Solution\(\frac{m}{n} + \frac{(m - 1)}{5n} - \frac{(m - 2)}{10n}\); \(\frac{10m + 2(m - 1) - 1(m - 2)}{10m}\)= \(\frac{10m + 2m - 2 - m + 2}{10n}\) = \(\frac{10m + 2m - m - 2 + 2}{10n}\) = \(\frac{11m}{10n}\) |
|
| 23. |
If \(\sqrt{72} + \sqrt{32} - 3 \sqrt{18} = x \sqrt{8}\), Find the value of x A. 1 B. \(\frac{3}{4}\) C. \(\frac{1}{2}\) D. \(\frac{1}{4}\) Detailed Solution\(\sqrt{2} + \sqrt{32} - 3\sqrt{18} = x\sqrt{8}\)= \(\sqrt{36 \times 2} + \sqrt{16 \times 2} - 3\sqrt{2 \times 9}\) = x\(\sqrt{2 \times 4}\) = 6\(\sqrt{2} + 4\sqrt{2} - 9\sqrt{2} = 2 \times \sqrt{2}\) \(\sqrt{2} (6 + 4 - 9) = 2x\sqrt{2}\) \(\sqrt{2} = 2x \sqrt{2}\) divide both sides by \(\sqrt{2}\) \(\frac{\sqrt{2}}{\sqrt{2}} = \frac{2 \times \sqrt{2}}{\sqrt{2}}\) 1 = 2x 2x = 1 x = \(\frac{1}{2}\) |
|
| 24. |
G varies directly as the square of H, If G is 4 when H is 3, find H when G = 100 A. 15 B. 25 C. 75 D. 225 Detailed SolutionG \(\alpha\) H2G = KH2 4 = K(3)2 4 = 9k; K = \(\frac{4}{9}\) 100 = \(\frac{4}{9}H^2\) 4H2 = 900 H2 = \(\frac{900}{4}\) H2 = 225 H = \(\sqrt{225}\) H = 15 |
|
| 25. |
Given that n(p) = 19, m(P \(\cup\) Q) = 38 and n(P \(\cap\) Q) = 7, Find n(C) A. 26 B. 31 C. 36 D. 50 Detailed Solutionn(P \(\cup\) Q) = m(P \(\cap\) C)38 = 19 = n(C) - 7 n(C) = 38 - 12 = 26 |
| 26. |
What must be added to (2x - 3y) to get (x - 2y)? A. 5y - x B. y - x C. x - 5x D. x - y Detailed SolutionWhat must be added to 2x - 3y = Difference between x - 2y and 2x - 3yx - 2y - 2y - (2x - 3y); x - 2y - 2x + 3y = x - 2x + 3y - 2y = y - x |
|
| 27. |
Simplify 1\(\frac{3}{4} - (2 \frac{1}{3} + 4)\) A. 3\(\frac{5}{12}\) B. 2\(\frac{7}{12}\) C. -4 \(\frac{7}{12}\) D. -5 \(\frac{7}{12}\) Detailed Solution1\(\frac{3}{4} - (2 \frac{1}{3} + 4)\) = \(\frac{7}{4} - (\frac{7}{3} + \frac{4}{1})\); \(\frac{7 + 12}{3}\)\(\frac{7}{4} - \frac{19}{3} = \frac{21 + 76}{12}\) = \(\frac{-55}{12} = -4 \frac{7}{12}\) |
|
| 28. |
Find the smaller value of x that satisfies the equation x2 + 7x + 10 = 0 A. -5 B. -2 C. 2 D. 5 Detailed Solutionx2 + 7x + 10 = 0x2 + 5x + 2x + 10 = 0 x(x + 5) + 2(x + 5) = 0 (x + 2)(x + 5) = 0 x + 2 = 0 or x + 5 = 0 x = -2 or x = -5 the smaller value x = -5 |
|
| 29. |
The perpendicular bisectors of the sides of an acute-angled triangle are drawn. Which of these statements is correct? They intersect A. on one of the vertices B. at a midpoint of a side C. inside the triangle D. outside the triangle |
C |
| 30. |
A rectangular garden measures 18.6m by 12.5m. Calculate, correct to three significant figures, the area of the garden A. 230m2 B. 231m2 C. 232m2 D. 233m2 Detailed SolutionA = L x B= (18.6 x 12.5)m2 = 232.5m2 = 233m2 |