Year :
2006
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
31 - 40 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
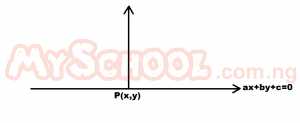
What is the locus of points equidistant from the lines ax + by + c = 0? A. A line bx - ay +q = 0 B. A line ax - by +q = 0 C. A line bx + ay +q = 0 D. A line ax + by +q = 0 Detailed Solution
∴Gradient of the line ax + by + c = 0 \(\implies by = -ax - c\) \(y = \frac{-a}{b}x - \frac{c}{b}\) \(Gradient = \frac{-a}{b}\) \(\therefore \text{The gradient of the perpendicular bisector} = \frac{b}{a}\) If P(x,y) is the point intersection of the two lines equation of the perpendicular becomes \(y - y_{1} = m(x - x_{1})\) \(y - y_{1} = \frac{b}{a}(x - x_{1})\) \(\frac{y - y_{1}}{x - x_{1}} = \frac{b}{a}\) \(ay - ay_{1} = bx - bx_{1}\) \(ay - bx + bx_{1} - ay_{1} = 0\) Let \(q = bx_{1} - ay_{1}\) \(\therefore \t |
|
| 32. |
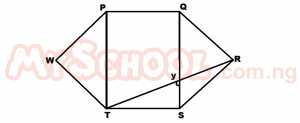
PQRSTW is a regular hexagon and QS intersects RT at V. Calculate ∠TVS A. 120o B. 90o C. 30o D. 60o Detailed Solution
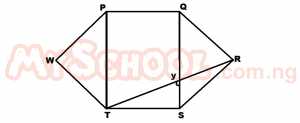 \(=\frac{(n-2)180}{n}\\ =\frac{(6-2)180}{6}\\ =\frac{(4)180}{6}\) = 120o ΔQSR is isosceles ∴ Q = S = 30o Also ΔTSR is isosceles ∴ T = R = 30o ∠TSV + ∠VSR = 120 ∠TSV + 30 = 120 ∠TSV = 120 - 30 ∠TSV = 90o ∴∴VTS + ∴VST + ∴TVS = 180 (sum of ∠s of a Δ) 30 + 90 + ∠TVS = 180 120 + ∠TVS = 180 ∠T |
|
| 33. |
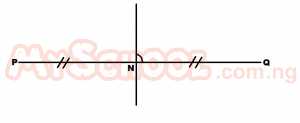
If the locus of the points which are equidistant from point P and Q meets line PQ at point N, then PN equals A. NQ B. 1/4NQ C. 2NQ D. 1/2NQ Detailed Solution
∴PN = NQ |
|
| 34. |
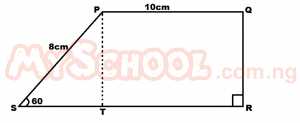
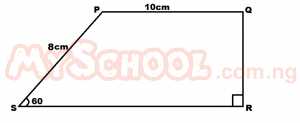 In the diagram above, PQ = 10 cm, PS = 8 cm and ∠PSR is 60o while ∠SRQ is a right angle. Find SR A. 14 cm B. 14√3 cm C. 10 cm D. 10√3 cm Detailed Solution
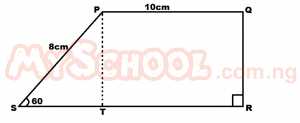 ST = 8cos 60 ST = 8 x 1/2 = 4 TR = 10 cm (opp. sides of a rectangle PQRT) SR = ST + TR SR = 4 + 10 SR = 14 cm |
|
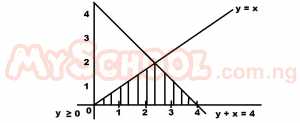
| 35. |
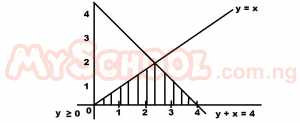 The solution set of the shaded area above is A. y ≥ 0, y ≥ x and y + x ≤ 4 B. y ≤ x, y + x ≤ 4 C. y + x ≥ 4, y ≤ x D. y ≤ x, y + x ≤ 4 and y ≥ 0 Detailed Solution
y + x = 4 implies y = 4 – x ∴y = 4 – x ∴y ≤ x, y + x ≤ 4 and y ≥ 0 |
|
| 36. |
A binary operation \(\oplus\) defined on the set of real number is such that x\(\oplus\)y = xy/6 for all x, y ∈ R. Find the inverse of 20 under this operation when the identity element is 6 A. 1/12 B. 10/3 C. 1/20 D. 9/5 Detailed Solutionx ⊕ y = xy/6 = xe/6 = xxe = 6x e = 6 x ⊕ y = xx1/6 where x1 = 20 x x 20/6 = 6 x = 36/20 x = 9/5 |
|
| 37. |
If p varies inversely as the cube of q and q varies directly as the square of r, what is the relationship between p and r? A. p varies directly as r3 B. p varies inversely as r6 C. p varies inversely as 6√P D. p varies directly as r6 Detailed SolutionP ∝ 1/q3P = K/q3 q3 = K/P q = K/p1/3 But q ∝ r2 q = Kr2 K/p1/3 = Kr2 r2 = K/p1/ |
|
| 38. |
A binary operation * on the set of rational numbers is defined as \(x \ast y = \frac{x^2 - y^2}{2xy}\). Find \(-5 \ast 3\) A. \(\frac{-8}{15}\) B. \(\frac{8}{15}\) C. \(\frac{17}{15}\) D. \(\frac{-17}{15}\) Detailed Solution\(x \ast y = \frac{x^2 - y^2}{2xy}\\=\frac{(x+y)(x-y)}{2xy}\\ -5 \ast 3 =\frac{(-5+3)(-5-3)}{2(-5\times3)}\\ =\frac{-2 \times -8}{2(-5\times3)}\\ =\frac{-8}{15}\) |
|
| 39. |
Find the value of k if the expression kx3 + x2 - 5x - 2 leaves a remainder 2 when it is divided by 2x + 1 A. 10 B. 8 C. -10 D. -8 Detailed SolutionF(x) = Q x D + RKx3 + x2 - 5x – 2 = Q(2x+1)+R If 2x+1 = 0 implies x = -1/2 ∴k(-1/2)3 + (-1/2)2 -5(-1/2) -2 = Q(2(-1/2) + 1) +2 K(-1/8) + 1/4 + 5/2 - 2 = Q(-1+1)+2 -k/8 + |
|
| 40. |
Solve the inequalities for which \(\frac{x+4}{3}-\frac{x-3}{2} < 4\) A. x < 7 B. x > -7 C. x < -7 D. x > 7 Detailed Solution\(\frac{x+4}{3}-\frac{x-3}{2} < 4\\\frac{(2(x+4))-(3(x-3))}{6}<4\) 2(x+4) – 3(x-3) < 4 x 6 2x + 8 – 3x+9 < 24 -x + 17 < 24 -x < 24 – 17 -x < 7 x > -7 |
| 31. |
What is the locus of points equidistant from the lines ax + by + c = 0? A. A line bx - ay +q = 0 B. A line ax - by +q = 0 C. A line bx + ay +q = 0 D. A line ax + by +q = 0 Detailed Solution
∴Gradient of the line ax + by + c = 0 \(\implies by = -ax - c\) \(y = \frac{-a}{b}x - \frac{c}{b}\) \(Gradient = \frac{-a}{b}\) \(\therefore \text{The gradient of the perpendicular bisector} = \frac{b}{a}\) If P(x,y) is the point intersection of the two lines equation of the perpendicular becomes \(y - y_{1} = m(x - x_{1})\) \(y - y_{1} = \frac{b}{a}(x - x_{1})\) \(\frac{y - y_{1}}{x - x_{1}} = \frac{b}{a}\) \(ay - ay_{1} = bx - bx_{1}\) \(ay - bx + bx_{1} - ay_{1} = 0\) Let \(q = bx_{1} - ay_{1}\) \(\therefore \t |
|
| 32. |
PQRSTW is a regular hexagon and QS intersects RT at V. Calculate ∠TVS A. 120o B. 90o C. 30o D. 60o Detailed Solution
 \(=\frac{(n-2)180}{n}\\ =\frac{(6-2)180}{6}\\ =\frac{(4)180}{6}\) = 120o ΔQSR is isosceles ∴ Q = S = 30o Also ΔTSR is isosceles ∴ T = R = 30o ∠TSV + ∠VSR = 120 ∠TSV + 30 = 120 ∠TSV = 120 - 30 ∠TSV = 90o ∴∴VTS + ∴VST + ∴TVS = 180 (sum of ∠s of a Δ) 30 + 90 + ∠TVS = 180 120 + ∠TVS = 180 ∠T |
|
| 33. |
If the locus of the points which are equidistant from point P and Q meets line PQ at point N, then PN equals A. NQ B. 1/4NQ C. 2NQ D. 1/2NQ Detailed Solution
∴PN = NQ |
|
| 34. |
 In the diagram above, PQ = 10 cm, PS = 8 cm and ∠PSR is 60o while ∠SRQ is a right angle. Find SR A. 14 cm B. 14√3 cm C. 10 cm D. 10√3 cm Detailed Solution
 ST = 8cos 60 ST = 8 x 1/2 = 4 TR = 10 cm (opp. sides of a rectangle PQRT) SR = ST + TR SR = 4 + 10 SR = 14 cm |
|
| 35. |
 The solution set of the shaded area above is A. y ≥ 0, y ≥ x and y + x ≤ 4 B. y ≤ x, y + x ≤ 4 C. y + x ≥ 4, y ≤ x D. y ≤ x, y + x ≤ 4 and y ≥ 0 Detailed Solution
y + x = 4 implies y = 4 – x ∴y = 4 – x ∴y ≤ x, y + x ≤ 4 and y ≥ 0 |
| 36. |
A binary operation \(\oplus\) defined on the set of real number is such that x\(\oplus\)y = xy/6 for all x, y ∈ R. Find the inverse of 20 under this operation when the identity element is 6 A. 1/12 B. 10/3 C. 1/20 D. 9/5 Detailed Solutionx ⊕ y = xy/6 = xe/6 = xxe = 6x e = 6 x ⊕ y = xx1/6 where x1 = 20 x x 20/6 = 6 x = 36/20 x = 9/5 |
|
| 37. |
If p varies inversely as the cube of q and q varies directly as the square of r, what is the relationship between p and r? A. p varies directly as r3 B. p varies inversely as r6 C. p varies inversely as 6√P D. p varies directly as r6 Detailed SolutionP ∝ 1/q3P = K/q3 q3 = K/P q = K/p1/3 But q ∝ r2 q = Kr2 K/p1/3 = Kr2 r2 = K/p1/ |
|
| 38. |
A binary operation * on the set of rational numbers is defined as \(x \ast y = \frac{x^2 - y^2}{2xy}\). Find \(-5 \ast 3\) A. \(\frac{-8}{15}\) B. \(\frac{8}{15}\) C. \(\frac{17}{15}\) D. \(\frac{-17}{15}\) Detailed Solution\(x \ast y = \frac{x^2 - y^2}{2xy}\\=\frac{(x+y)(x-y)}{2xy}\\ -5 \ast 3 =\frac{(-5+3)(-5-3)}{2(-5\times3)}\\ =\frac{-2 \times -8}{2(-5\times3)}\\ =\frac{-8}{15}\) |
|
| 39. |
Find the value of k if the expression kx3 + x2 - 5x - 2 leaves a remainder 2 when it is divided by 2x + 1 A. 10 B. 8 C. -10 D. -8 Detailed SolutionF(x) = Q x D + RKx3 + x2 - 5x – 2 = Q(2x+1)+R If 2x+1 = 0 implies x = -1/2 ∴k(-1/2)3 + (-1/2)2 -5(-1/2) -2 = Q(2(-1/2) + 1) +2 K(-1/8) + 1/4 + 5/2 - 2 = Q(-1+1)+2 -k/8 + |
|
| 40. |
Solve the inequalities for which \(\frac{x+4}{3}-\frac{x-3}{2} < 4\) A. x < 7 B. x > -7 C. x < -7 D. x > 7 Detailed Solution\(\frac{x+4}{3}-\frac{x-3}{2} < 4\\\frac{(2(x+4))-(3(x-3))}{6}<4\) 2(x+4) – 3(x-3) < 4 x 6 2x + 8 – 3x+9 < 24 -x + 17 < 24 -x < 24 – 17 -x < 7 x > -7 |