Year :
2006
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
21 - 30 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 21. |
Evaluate \(\frac{2}{6-5\sqrt{3}}\) A. \(-\left(\frac{12}{39}-\frac{10\sqrt{3}}{39}\right)\) B. \(\frac{12}{39}-\frac{10\sqrt{3}}{39}\) C. \(-\left(\frac{12}{39}+\frac{10\sqrt{3}}{39}\right)\) D. \(\frac{12}{39}+\frac{10\sqrt{3}}{39}\) Detailed Solution\(\frac{2}{6-5\sqrt{3}} = \frac{2}{6-5\sqrt{3}} \times \frac{6+5\sqrt{3}}{6+5\sqrt{3}}\\=\frac{2(6+5\sqrt{3})}{(6-5\sqrt{3})(6+5\sqrt{3})}\\ =\frac{12+10-\sqrt{3}}{36-25(3)}\\ =\frac{12+10-\sqrt{3}}{36-75}\\ =\frac{12+10-\sqrt{3}}{-39}\\ =-\left(\frac{12}{39}-\frac{10\sqrt{3}}{39}\right)\) |
|
| 22. |
Compute 1100112 + 111112 A. 10010102 B. 10100102 C. 10001102 D. 10001002 Detailed Solution1100112 + 111112 = 10100102 |
|
| 23. |
Simplify \((25)^{\frac{-1}{2}} \times (27)^{\frac{1}{3}} + (121)^{\frac{-1}{2}} \times (625)^{\frac{-1}{4}}\) A. 34/55 B. 9/11 C. 14/5 D. 3/275 Detailed Solution(25)\(^{\frac{-1}{2}}\) x (27)\(^{\frac{1}{3}}\) + (121)\(^{\frac{-1}{2}}\) x (625)\(^{\frac{-1}{4}}\)5\(^{2 \times \frac{-1}{2}}\) x 3\(^{3 \times \frac{1}{3}}\) + 11\(^{2 \times \frac{-1}{2}}\) x 5\(^{4 \times \frac{-1}{4}}\) 5\(^{-1}\) x 3\(^1\) x 11\(^{-1}\) x 5\(^{-1}\) \(\frac{1}{5} \times \frac{3}{1} + \frac{1}{11} \times \frac{1}{5}\) \(\frac{3}{5} + \frac{1}{55} = \frac{33+1}{55}\) = \(\frac{34}{55}\) |
|
| 24. |
Convert 2232\(_4\) to base six A. 4506 B. 2546 C. 5536 D. 5406 Detailed Solution1st convert to base 102232\(_4\) = 2 x 4\(^3\) + 2 x 4\(^2\) + 3 x 4\(^1\) + 2 x 4\(^0\) = 2 x 64 + 2 x 16 + 3 x 4 + 2 x 1 = 128 + 32 + 12 + 2 = 174 convert to base 6 6/174 6/29 R 0 6/4 R 5 6/0 R 4 = 450\(_6\) |
|
| 25. |
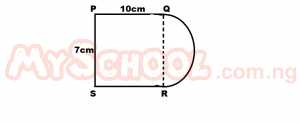 In the diagram above, QR is in the diameter of the semicircle QR. Find the area of the figure to the nearest whole number. [\(\pi = \frac{22}{7}\)] A. 89 cm2 B. 70 cm2 C. 90 cm2 D. 80 cm2 Detailed SolutionArea of rectangle PQRS = \(10 \times 7 = 70cm^2\)Area of semi-circle: \(\frac{\pi r^{2}}{2}\) r = \(\frac{7}{2} cm\) Area of semi-circle = \(\frac{1}{2} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) = \(\frac{77}{4} = 18.75 cm^{2}\) Area of figure = \((70 + 18.75) cm^{2}\) = 88.75 cm\(^{2} \approxeq\) 89 cm\(^{2}\) |
|
| 26. |
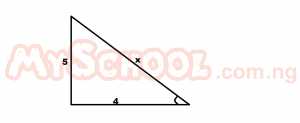
If tan θ = 5/4, find sin2θ - cos2θ. A. 5/4 B. 41/9 C. 9/41 D. 1 Detailed Solution
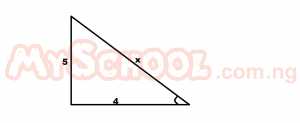 x2 = 52 + 42 = 25 + 16 = 41 x = √41 sin2θ - cos2θ = (5/√41)2 - (4/√41)2 = 25/41 - 16/41 = |
|
| 27. |
PQ and RS are two parallel lines. If the coordinates of P, Q, R, S are (1,q), (3,2), (3,4), (5,2q) respectively, find the value of q A. 3 B. 4 C. 1 D. 2 Detailed SolutionGradient PQ, P(1,q) and Q(3,2)\(=\frac{(2-q)}{(3-1)} = \frac{(2-q)}{2}\) Gradient of RS : R(3,4) and S(5,2q) \(= \frac{(2q-4)}{(5-3)}= \frac{(2q-4)}{2} = \frac{2(q-2)}{2}\) = q-2 Since PQ and RS are parallel, their gradients are equal \(∴ \frac{(2-q)}{2} = q-2\) 2-q = 2(q-2) 2-q = 2q-4 2+4 = 2q+q 6 = 3q q = 2 |
|
| 28. |
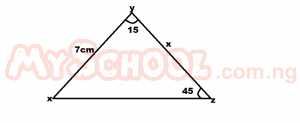
In triangle XYZ, ∠XYZ = 15o, ∠XZY = 45o and lXYl = 7 cm. Find lYZl. A. 14√2 cm B. \(7\left(\frac{\sqrt{6}}{2}\right)\) C. 7√2 cm D. 7 cm Detailed Solution
 = 180 - 60 = 120o Using sine rule \(\frac{x}{sinx}=\frac{7}{sinz}\\ \frac{x}{sin 120}=\frac{7}{sin 45}\\ x=\frac{7 sin 120}{sin45}\\ x=\frac{7sin(180-120)}{sin 45}\\ x=\frac{7 sin 60}{sin 45}=\left(7\left(\frac{\sqrt{3}}{2}\right)\div \frac{1}{\sqrt{2}}\right)\\ x =\left(7\left(\frac{\sqrt{3}}{2}\right)\div \frac{1}{\sqrt{2}}\right)\\ x = 7\left(\frac{\sqrt{6}}{2}\right)\) |
|
| 29. |
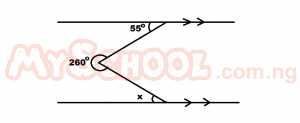 In the diagram above, find the value of x A. 55o B. 50o C. 45o D. 40o Detailed Solution
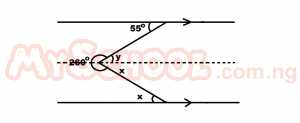 x = x (same reason) 260 + y + x = 360 (∠s at a point) 260 + 55 + x = 360 315 + x = 360 x = 360 - 315 x = 45o |
|
| 30. |
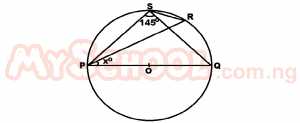 In the diagram above, POQ is a diameter of the circle PQRS. If ∠PSR = 145°, find x° A. 55o B. 45o C. 35o D. 25o Detailed Solution
∠PSQ + ∠QSR = 145° 90 + ∠QSR = 145 ∠QSR = 145 - 90 ∠QSR = 55° BUt x° = ∠QSR (∠s in the same segment) ∴x° = 55° |
| 21. |
Evaluate \(\frac{2}{6-5\sqrt{3}}\) A. \(-\left(\frac{12}{39}-\frac{10\sqrt{3}}{39}\right)\) B. \(\frac{12}{39}-\frac{10\sqrt{3}}{39}\) C. \(-\left(\frac{12}{39}+\frac{10\sqrt{3}}{39}\right)\) D. \(\frac{12}{39}+\frac{10\sqrt{3}}{39}\) Detailed Solution\(\frac{2}{6-5\sqrt{3}} = \frac{2}{6-5\sqrt{3}} \times \frac{6+5\sqrt{3}}{6+5\sqrt{3}}\\=\frac{2(6+5\sqrt{3})}{(6-5\sqrt{3})(6+5\sqrt{3})}\\ =\frac{12+10-\sqrt{3}}{36-25(3)}\\ =\frac{12+10-\sqrt{3}}{36-75}\\ =\frac{12+10-\sqrt{3}}{-39}\\ =-\left(\frac{12}{39}-\frac{10\sqrt{3}}{39}\right)\) |
|
| 22. |
Compute 1100112 + 111112 A. 10010102 B. 10100102 C. 10001102 D. 10001002 Detailed Solution1100112 + 111112 = 10100102 |
|
| 23. |
Simplify \((25)^{\frac{-1}{2}} \times (27)^{\frac{1}{3}} + (121)^{\frac{-1}{2}} \times (625)^{\frac{-1}{4}}\) A. 34/55 B. 9/11 C. 14/5 D. 3/275 Detailed Solution(25)\(^{\frac{-1}{2}}\) x (27)\(^{\frac{1}{3}}\) + (121)\(^{\frac{-1}{2}}\) x (625)\(^{\frac{-1}{4}}\)5\(^{2 \times \frac{-1}{2}}\) x 3\(^{3 \times \frac{1}{3}}\) + 11\(^{2 \times \frac{-1}{2}}\) x 5\(^{4 \times \frac{-1}{4}}\) 5\(^{-1}\) x 3\(^1\) x 11\(^{-1}\) x 5\(^{-1}\) \(\frac{1}{5} \times \frac{3}{1} + \frac{1}{11} \times \frac{1}{5}\) \(\frac{3}{5} + \frac{1}{55} = \frac{33+1}{55}\) = \(\frac{34}{55}\) |
|
| 24. |
Convert 2232\(_4\) to base six A. 4506 B. 2546 C. 5536 D. 5406 Detailed Solution1st convert to base 102232\(_4\) = 2 x 4\(^3\) + 2 x 4\(^2\) + 3 x 4\(^1\) + 2 x 4\(^0\) = 2 x 64 + 2 x 16 + 3 x 4 + 2 x 1 = 128 + 32 + 12 + 2 = 174 convert to base 6 6/174 6/29 R 0 6/4 R 5 6/0 R 4 = 450\(_6\) |
|
| 25. |
 In the diagram above, QR is in the diameter of the semicircle QR. Find the area of the figure to the nearest whole number. [\(\pi = \frac{22}{7}\)] A. 89 cm2 B. 70 cm2 C. 90 cm2 D. 80 cm2 Detailed SolutionArea of rectangle PQRS = \(10 \times 7 = 70cm^2\)Area of semi-circle: \(\frac{\pi r^{2}}{2}\) r = \(\frac{7}{2} cm\) Area of semi-circle = \(\frac{1}{2} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) = \(\frac{77}{4} = 18.75 cm^{2}\) Area of figure = \((70 + 18.75) cm^{2}\) = 88.75 cm\(^{2} \approxeq\) 89 cm\(^{2}\) |
| 26. |
If tan θ = 5/4, find sin2θ - cos2θ. A. 5/4 B. 41/9 C. 9/41 D. 1 Detailed Solution
 x2 = 52 + 42 = 25 + 16 = 41 x = √41 sin2θ - cos2θ = (5/√41)2 - (4/√41)2 = 25/41 - 16/41 = |
|
| 27. |
PQ and RS are two parallel lines. If the coordinates of P, Q, R, S are (1,q), (3,2), (3,4), (5,2q) respectively, find the value of q A. 3 B. 4 C. 1 D. 2 Detailed SolutionGradient PQ, P(1,q) and Q(3,2)\(=\frac{(2-q)}{(3-1)} = \frac{(2-q)}{2}\) Gradient of RS : R(3,4) and S(5,2q) \(= \frac{(2q-4)}{(5-3)}= \frac{(2q-4)}{2} = \frac{2(q-2)}{2}\) = q-2 Since PQ and RS are parallel, their gradients are equal \(∴ \frac{(2-q)}{2} = q-2\) 2-q = 2(q-2) 2-q = 2q-4 2+4 = 2q+q 6 = 3q q = 2 |
|
| 28. |
In triangle XYZ, ∠XYZ = 15o, ∠XZY = 45o and lXYl = 7 cm. Find lYZl. A. 14√2 cm B. \(7\left(\frac{\sqrt{6}}{2}\right)\) C. 7√2 cm D. 7 cm Detailed Solution
 = 180 - 60 = 120o Using sine rule \(\frac{x}{sinx}=\frac{7}{sinz}\\ \frac{x}{sin 120}=\frac{7}{sin 45}\\ x=\frac{7 sin 120}{sin45}\\ x=\frac{7sin(180-120)}{sin 45}\\ x=\frac{7 sin 60}{sin 45}=\left(7\left(\frac{\sqrt{3}}{2}\right)\div \frac{1}{\sqrt{2}}\right)\\ x =\left(7\left(\frac{\sqrt{3}}{2}\right)\div \frac{1}{\sqrt{2}}\right)\\ x = 7\left(\frac{\sqrt{6}}{2}\right)\) |
|
| 29. |
 In the diagram above, find the value of x A. 55o B. 50o C. 45o D. 40o Detailed Solution
 x = x (same reason) 260 + y + x = 360 (∠s at a point) 260 + 55 + x = 360 315 + x = 360 x = 360 - 315 x = 45o |
|
| 30. |
 In the diagram above, POQ is a diameter of the circle PQRS. If ∠PSR = 145°, find x° A. 55o B. 45o C. 35o D. 25o Detailed Solution
∠PSQ + ∠QSR = 145° 90 + ∠QSR = 145 ∠QSR = 145 - 90 ∠QSR = 55° BUt x° = ∠QSR (∠s in the same segment) ∴x° = 55° |