Year :
2006
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
11 - 20 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 11. |
Find the value of x for which the function 3x3 - 9x is minimum A. zero B. 2 C. 3 D. 5 Detailed Solutiony = 3x3 - 9x2dy/dx = 9x2 - 18x As dy/dx = 0 9x2 - 18x = 0 9x(x-2) = 0 9x = 0 which implies x = 0 x-2 = 0 implies x = 2 d2y/dx2 = 18x - 18 when x = 0 d2y/dx2 < 0 ∴ x is is minimum when x = 2d2y/dx2 = 18 ∴ > 0 x is minimum |
|
| 12. |
If dy/dx = x + cos x, find y A. x2 - sin x + c B. x2 + sin x + c C. x2/2 - sin x + c D. x2/2 + sin x + c Detailed Solutiondy/dx = x + cos xy = ∫(x + cos x)dx y = 1/2x2 + sin x + C |
|
| 13. |
Differentiate (cos θ - sin θ)\(^2\) A. -2 cos 2θ B. -2 sin2θ C. 1 - 2 cos 2θ D. 1 - 2 sin 2θ Detailed Solutiony = (cosθ - sinθ)dy/dx = 2(cosθ - sinθ)(-sinθ - cosθ) dy/dx = 2(-cosθsinθ - cos2θ + sin2θ) dy/dx = 2(- cos\(^2\)θ + sin\(^2\)θ) = -2(cos\(^2\)θ - sin\(^2\)θ) = -2(1 - 2sin\(^2\)θ) = -2cos2θ |
|
| 14. |
Evaluate \(\int_{-4}^0(1 - 2x)dx\) A. -16 B. -20 C. 20 D. 10 Detailed Solution\(\int_{-4}^0(1 - 2x)dx=[x-x^2]_{-4}^0\\= (0 - 0 + C) - (-4(-4)^2 + C)\\= C - (-4-16+C)\\ = C-(-20+C)\\ = C+20-C\\ = 20\) |
|
| 15. |
Simplify \(\frac{\frac{7}{9}-\frac{2}{3}}{\frac{1}{3}+\frac{\frac{2}{5}}{\frac{4}{5}}}\) A. \(\frac{11}{12}\) B. \(\frac{5}{6}\) C. \(\frac{1}{5}\) D. \(\frac{2}{15}\) Detailed Solution\(\frac{\frac{7}{9}-\frac{2}{3}}{\frac{1}{3}+\frac{\frac{2}{5}}{\frac{4}{5}}}\\=\frac{\frac{7-6}{9}}{\frac{1}{3}+\frac{\frac{2}{5}}{\frac{4}{5}}}\\ =\frac{\frac{1}{9}}{\frac{1}{3}+\left(\frac{2}{5}\times \frac{5}{4}\right)}\\ =\frac{\frac{1}{9}}{\frac{1}{3}+\frac{1}{2}}\ =\frac{\frac{1}{9}}{\frac{2+3}{6}}\\ =\frac{\frac{1}{9}}{\frac{5}{6}}\\ =\frac{1}{9}\times\frac{6}{5}\\ =\frac{2}{15}\) |
|
| 16. |
If m:n = 13:11, find m\(^2\) - n\(^2\) : (m + n)\(^2\) A. 1:11 B. 1:13 C. 1:10 D. 1:12 Detailed Solutionm : n = 13 : 11m\(^2\) - n\(^2\) : (m + n)2 = 13\(^2\) - 11\(^2\) : (13 + 11)\(^2\) = 169 - 121 : 24\(^2\) = 48 : 576 = 1 : 12 |
|
| 17. |
Calculate the logarithm to base 9 of 3-4 * 92 * (81)-1 A. 2 B. zero C. -2 D. -4 Detailed Solution\(3^{-4}\times 9^2 \times 81^{-1}\\=log_9 (3^{-4}\times 9^2 \times 81^{-1})\\ =log_9 \left(\frac{1}{3^4}\times 9^2 \times \frac{1}{81}\right)\\ =log_9 \left(\frac{1}{81}\times \frac{81}{1}\times \frac{1}{81}\right)\\ =log_9 \frac{1}{81}\\ =log_9 \frac{1}{9^2}\\ =log_9 9^{-2}\\ =-2log_9 9\\ -2 \times 1\\ =-2\) |
|
| 18. |
If (K2)\(_6\) * 3\(_6\) = 3\(_5\)(K4)\(_5\), what is the value of k? A. 1 B. 4 C. 3 D. 2 Detailed Solution(K2)\(_6\) * 3\(_6\) = 3\(_5\)(K4)\(_5\)(K*6\(^1\) + 2*6\(^0\)) 3*6\(^0\) = 3*5\(^0\)(K*5\(^1\) + 4*5\(^0\)) 3(6K + 2) = 3(5K + 4) 6K + 2 = 5K + 4 6K - 5K = 4 - 2 K = 2 |
|
| 19. |
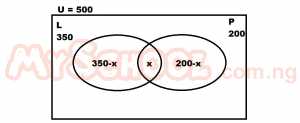
In a small village of 500 people, 350 speak the local language while 200 speak pidgin English. What percentage of the population speak both. A. 30% B. 10% C. 50% D. 14% Detailed Solution
 n(L) only = 350 - x n(P) only = 200 - x ∴350 - x + x + 200 - x = 500 550 - x = 500 x = 550 - 500 x = 50 speak both ∴x% = (50/500) * (100/1) = 10% |
|
| 20. |
Find the tax on an income of N20,000 if no tax is paid on the first N10,000 and tax is paid at N50 in N1000 on the next N5000 and at N55 in N1000 on the remainder A. N500 B. N552 C. N255 D. N525 Detailed SolutionN20,000 - N10,000 = N10,0001st tax on N5000 at N50 per N1000 = 5*50 = N250 2nd tax on the remaining N5000 at N55 per N1000 = 5*55 = N275 Total tax paid = N250 + N275 = N525 |
| 11. |
Find the value of x for which the function 3x3 - 9x is minimum A. zero B. 2 C. 3 D. 5 Detailed Solutiony = 3x3 - 9x2dy/dx = 9x2 - 18x As dy/dx = 0 9x2 - 18x = 0 9x(x-2) = 0 9x = 0 which implies x = 0 x-2 = 0 implies x = 2 d2y/dx2 = 18x - 18 when x = 0 d2y/dx2 < 0 ∴ x is is minimum when x = 2d2y/dx2 = 18 ∴ > 0 x is minimum |
|
| 12. |
If dy/dx = x + cos x, find y A. x2 - sin x + c B. x2 + sin x + c C. x2/2 - sin x + c D. x2/2 + sin x + c Detailed Solutiondy/dx = x + cos xy = ∫(x + cos x)dx y = 1/2x2 + sin x + C |
|
| 13. |
Differentiate (cos θ - sin θ)\(^2\) A. -2 cos 2θ B. -2 sin2θ C. 1 - 2 cos 2θ D. 1 - 2 sin 2θ Detailed Solutiony = (cosθ - sinθ)dy/dx = 2(cosθ - sinθ)(-sinθ - cosθ) dy/dx = 2(-cosθsinθ - cos2θ + sin2θ) dy/dx = 2(- cos\(^2\)θ + sin\(^2\)θ) = -2(cos\(^2\)θ - sin\(^2\)θ) = -2(1 - 2sin\(^2\)θ) = -2cos2θ |
|
| 14. |
Evaluate \(\int_{-4}^0(1 - 2x)dx\) A. -16 B. -20 C. 20 D. 10 Detailed Solution\(\int_{-4}^0(1 - 2x)dx=[x-x^2]_{-4}^0\\= (0 - 0 + C) - (-4(-4)^2 + C)\\= C - (-4-16+C)\\ = C-(-20+C)\\ = C+20-C\\ = 20\) |
|
| 15. |
Simplify \(\frac{\frac{7}{9}-\frac{2}{3}}{\frac{1}{3}+\frac{\frac{2}{5}}{\frac{4}{5}}}\) A. \(\frac{11}{12}\) B. \(\frac{5}{6}\) C. \(\frac{1}{5}\) D. \(\frac{2}{15}\) Detailed Solution\(\frac{\frac{7}{9}-\frac{2}{3}}{\frac{1}{3}+\frac{\frac{2}{5}}{\frac{4}{5}}}\\=\frac{\frac{7-6}{9}}{\frac{1}{3}+\frac{\frac{2}{5}}{\frac{4}{5}}}\\ =\frac{\frac{1}{9}}{\frac{1}{3}+\left(\frac{2}{5}\times \frac{5}{4}\right)}\\ =\frac{\frac{1}{9}}{\frac{1}{3}+\frac{1}{2}}\ =\frac{\frac{1}{9}}{\frac{2+3}{6}}\\ =\frac{\frac{1}{9}}{\frac{5}{6}}\\ =\frac{1}{9}\times\frac{6}{5}\\ =\frac{2}{15}\) |
| 16. |
If m:n = 13:11, find m\(^2\) - n\(^2\) : (m + n)\(^2\) A. 1:11 B. 1:13 C. 1:10 D. 1:12 Detailed Solutionm : n = 13 : 11m\(^2\) - n\(^2\) : (m + n)2 = 13\(^2\) - 11\(^2\) : (13 + 11)\(^2\) = 169 - 121 : 24\(^2\) = 48 : 576 = 1 : 12 |
|
| 17. |
Calculate the logarithm to base 9 of 3-4 * 92 * (81)-1 A. 2 B. zero C. -2 D. -4 Detailed Solution\(3^{-4}\times 9^2 \times 81^{-1}\\=log_9 (3^{-4}\times 9^2 \times 81^{-1})\\ =log_9 \left(\frac{1}{3^4}\times 9^2 \times \frac{1}{81}\right)\\ =log_9 \left(\frac{1}{81}\times \frac{81}{1}\times \frac{1}{81}\right)\\ =log_9 \frac{1}{81}\\ =log_9 \frac{1}{9^2}\\ =log_9 9^{-2}\\ =-2log_9 9\\ -2 \times 1\\ =-2\) |
|
| 18. |
If (K2)\(_6\) * 3\(_6\) = 3\(_5\)(K4)\(_5\), what is the value of k? A. 1 B. 4 C. 3 D. 2 Detailed Solution(K2)\(_6\) * 3\(_6\) = 3\(_5\)(K4)\(_5\)(K*6\(^1\) + 2*6\(^0\)) 3*6\(^0\) = 3*5\(^0\)(K*5\(^1\) + 4*5\(^0\)) 3(6K + 2) = 3(5K + 4) 6K + 2 = 5K + 4 6K - 5K = 4 - 2 K = 2 |
|
| 19. |
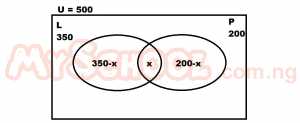
In a small village of 500 people, 350 speak the local language while 200 speak pidgin English. What percentage of the population speak both. A. 30% B. 10% C. 50% D. 14% Detailed Solution
 n(L) only = 350 - x n(P) only = 200 - x ∴350 - x + x + 200 - x = 500 550 - x = 500 x = 550 - 500 x = 50 speak both ∴x% = (50/500) * (100/1) = 10% |
|
| 20. |
Find the tax on an income of N20,000 if no tax is paid on the first N10,000 and tax is paid at N50 in N1000 on the next N5000 and at N55 in N1000 on the remainder A. N500 B. N552 C. N255 D. N525 Detailed SolutionN20,000 - N10,000 = N10,0001st tax on N5000 at N50 per N1000 = 5*50 = N250 2nd tax on the remaining N5000 at N55 per N1000 = 5*55 = N275 Total tax paid = N250 + N275 = N525 |