Year :
1999
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
31 - 40 of 45 Questions
| # | Question | Ans | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 31. |
 The shaded portion in the graph above is represented by A. y + x - x3 ≥ 0, y - x ≤ 0 B. y - x + x3 ≥ 0, y - x ≤ 0 C. y + x - x3 ≤ 0, y + x ≥ 0 D. y - x + x3 ≤ 0, y + x ≥ 0 Detailed Solutiony + x - x2 ≥ 0y = x3 - x on x axis, y = 0 ∴x2 - x = 0 x(x2 - 1) = 0 x = 0 or x2 - 1 = 0 x2 = 1 x = +/-1 ∴ x = -1, 0 and 1 which are the roots of the equation y + x - x2 ≥ 0 Also y - x ≤ 0 => y ≤ 0 + x ∴ the region where y ≤ 0 |
||||||||
| 32. |
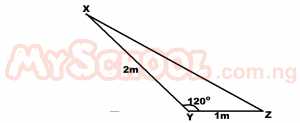 Find the length XZ in the triangle above. A. √7 m B. √6 m C. √5 m D. √3 m Detailed SolutionXY2 = XY2 + Y2 - 2XY.YZ cos 120XZ2 = 22 + 12 - 2 x 2 1 cos 120 = 4 + 1 -2 x 2 x 1 x -cos(180 - 120) = 4 + 1 + 4 cos 60 = 5 + 4 x 1/2 = 5 + 2 = 7 XY = √7 m |
||||||||
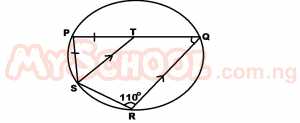
| 33. |
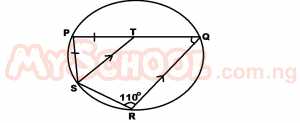 In the figure above, PQRS is a circle with ST//RQ. Find the value of x PT = PS. A. 70o B. 55o C. 40o D. 35o Detailed Solution
 ^P = 180 - 110 (opp ∠s of a cyclic quad) ^P = 70 In ΔPTS, ^S = ^T (base ∠s of Isc Δ) ∴^T = (180-70) / 2 = 110/2 = 55o But ^T x(corr ∠) ∴x =55 |
||||||||
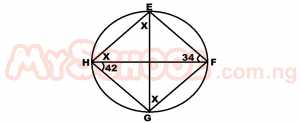
| 34. |
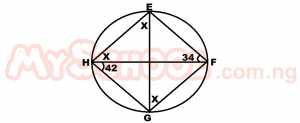 In the diagram above, EFGH is a cyclic quadrilateral in which EH//FG, EG and FH are chords. If ∠FHG = 42o and ∠EFH = 34o, calculate ∠HEG A. 34o B. 42o C. 52o D. 76o Detailed Solution
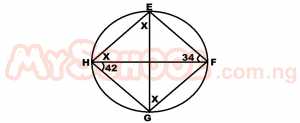 = 34o ∠HEG = ∠HFG(∠s in same segment) = X also ∠HFG = ∠EHF (alternate ∠s) But ∠EHG + ∠EFG =180(opp sof a cyclic quad) 42 + x + 34 + x = 180 2x + 76 = 180 2x = 180 - 76 2x = 104 x = 52o |
||||||||
| 35. |
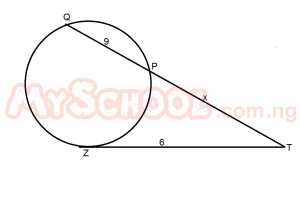 In the figure above, TZ is tangent to the circle QPZ. Find x if TZ = 6 units and PQ = 9 units A. 3 B. 4 C. 5 D. 6 Detailed Solution62 = 9 x χ36 = 9χ χ = 36/9 χ = 4 |
||||||||
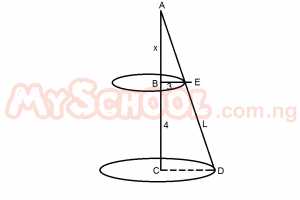
| 36. |
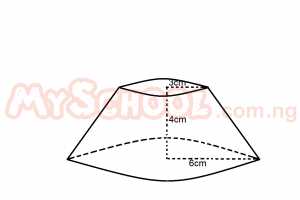 Find the value of l in the frustrum above A. 5cm B. 6cm C. 7cm D. 8cm Detailed Solution

6x = 3(x+4) 6 |
||||||||
| 37. |
 The diagram above is the graph of y = x2, the shaded area is A. 64 square units B. 128/3 square units C. 64/3 square units D. 32 square units Detailed Solution\(\int_0 ^4 x^2 dx = \left[\frac{1}{3}x^2+C\right]_0 ^4\\=\frac{1}{3}\times 4^3 - \frac{1}{3}\times 0^3\\ =\frac{64}{3}-0\\ =\frac{64}{3}\)sq units |
||||||||
| 38. |
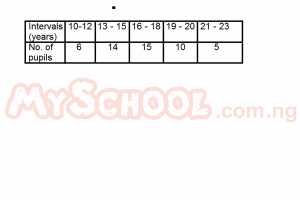 The table above shows the frequency distribution of the ages (in years) of pupils in a certain secondary school. What percentage of the total number of pupils is over 15 years but less than 21 years? A. 35% B. 45% C. 50% D. 60% Detailed Solution
 age = 25/50 x 100/1 = 50% |
||||||||
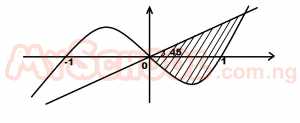
| 39. |
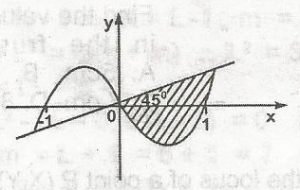 The shaded portion in the graph is represented by A. y + x - x \(\leq\) 0, y - x \(\leq\) 0 B. y - x + x, 3 \(\leq\) 0, y - x \(\geq\) 0 C. y + x - 3 \(\geq\) 0, y + x \(\leq\) 0 D. y - x + x3 \(\geq\) 0, y + x \(\leq\) 0 |
C |
|||||||
| 40. |
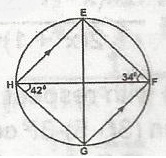 In the diagram, EFGH is a cyclic quadrilateral in which EH || FG, EG and FH are chords. If < FHG = 424o and < EFH = 34o A. 34o B. 42o C. 52o D. 76o Detailed Solution< EFH = < EGH = 34o (angles n the same segment)< GHF = < GEF = 42o(angles in the same segment) < FOG = 42 + 34 = 76(exterior angle) < FOG = < EOH = 76(vertically opposite angle) < EDO = 90o, < DOE = \(\frac{76}{2}\) = 38o < HEG = 90o - 38o = 52o |
| 31. |
 The shaded portion in the graph above is represented by A. y + x - x3 ≥ 0, y - x ≤ 0 B. y - x + x3 ≥ 0, y - x ≤ 0 C. y + x - x3 ≤ 0, y + x ≥ 0 D. y - x + x3 ≤ 0, y + x ≥ 0 Detailed Solutiony + x - x2 ≥ 0y = x3 - x on x axis, y = 0 ∴x2 - x = 0 x(x2 - 1) = 0 x = 0 or x2 - 1 = 0 x2 = 1 x = +/-1 ∴ x = -1, 0 and 1 which are the roots of the equation y + x - x2 ≥ 0 Also y - x ≤ 0 => y ≤ 0 + x ∴ the region where y ≤ 0 |
|
| 32. |
 Find the length XZ in the triangle above. A. √7 m B. √6 m C. √5 m D. √3 m Detailed SolutionXY2 = XY2 + Y2 - 2XY.YZ cos 120XZ2 = 22 + 12 - 2 x 2 1 cos 120 = 4 + 1 -2 x 2 x 1 x -cos(180 - 120) = 4 + 1 + 4 cos 60 = 5 + 4 x 1/2 = 5 + 2 = 7 XY = √7 m |
|
| 33. |
 In the figure above, PQRS is a circle with ST//RQ. Find the value of x PT = PS. A. 70o B. 55o C. 40o D. 35o Detailed Solution
 ^P = 180 - 110 (opp ∠s of a cyclic quad) ^P = 70 In ΔPTS, ^S = ^T (base ∠s of Isc Δ) ∴^T = (180-70) / 2 = 110/2 = 55o But ^T x(corr ∠) ∴x =55 |
|
| 34. |
 In the diagram above, EFGH is a cyclic quadrilateral in which EH//FG, EG and FH are chords. If ∠FHG = 42o and ∠EFH = 34o, calculate ∠HEG A. 34o B. 42o C. 52o D. 76o Detailed Solution
 = 34o ∠HEG = ∠HFG(∠s in same segment) = X also ∠HFG = ∠EHF (alternate ∠s) But ∠EHG + ∠EFG =180(opp sof a cyclic quad) 42 + x + 34 + x = 180 2x + 76 = 180 2x = 180 - 76 2x = 104 x = 52o |
|
| 35. |
 In the figure above, TZ is tangent to the circle QPZ. Find x if TZ = 6 units and PQ = 9 units A. 3 B. 4 C. 5 D. 6 Detailed Solution62 = 9 x χ36 = 9χ χ = 36/9 χ = 4 |
| 36. |
 Find the value of l in the frustrum above A. 5cm B. 6cm C. 7cm D. 8cm Detailed Solution

6x = 3(x+4) 6 |
||||||||
| 37. |
 The diagram above is the graph of y = x2, the shaded area is A. 64 square units B. 128/3 square units C. 64/3 square units D. 32 square units Detailed Solution\(\int_0 ^4 x^2 dx = \left[\frac{1}{3}x^2+C\right]_0 ^4\\=\frac{1}{3}\times 4^3 - \frac{1}{3}\times 0^3\\ =\frac{64}{3}-0\\ =\frac{64}{3}\)sq units |
||||||||
| 38. |
 The table above shows the frequency distribution of the ages (in years) of pupils in a certain secondary school. What percentage of the total number of pupils is over 15 years but less than 21 years? A. 35% B. 45% C. 50% D. 60% Detailed Solution
 age = 25/50 x 100/1 = 50% |
||||||||
| 39. |
 The shaded portion in the graph is represented by A. y + x - x \(\leq\) 0, y - x \(\leq\) 0 B. y - x + x, 3 \(\leq\) 0, y - x \(\geq\) 0 C. y + x - 3 \(\geq\) 0, y + x \(\leq\) 0 D. y - x + x3 \(\geq\) 0, y + x \(\leq\) 0 |
C |
|||||||
| 40. |
 In the diagram, EFGH is a cyclic quadrilateral in which EH || FG, EG and FH are chords. If < FHG = 424o and < EFH = 34o A. 34o B. 42o C. 52o D. 76o Detailed Solution< EFH = < EGH = 34o (angles n the same segment)< GHF = < GEF = 42o(angles in the same segment) < FOG = 42 + 34 = 76(exterior angle) < FOG = < EOH = 76(vertically opposite angle) < EDO = 90o, < DOE = \(\frac{76}{2}\) = 38o < HEG = 90o - 38o = 52o |