Year :
2020
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
21 - 30 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 21. |
A man is five times as old as his son. In four years' time, the product of their ages would be 340. If the son's age is y, express the product of their ages in terms of y. A. 5y\(^2 - 16y - 380 = 0\) B. 5y\(^2 - 24y - 380 = 0\) C. 5y\(^2 - 16y - 330 = 0\) D. 5y\(^2 - 24y - 324 = 0\) Detailed SolutionMan = x, Son = yx = 5y (x + 4)(y + 4) = 350 (5y + 4)(y + 4) = 340 5y\(^2\) + 20y + 4y + 16 - 240 = 0 5y\(^2\) + 24y - 324 = 0 |
|
| 22. |
Simplify; \(\frac{a}{b} - \frac{a}{a} - \frac{c}{b}\) A. \(\frac{a - b + c}{ab}\) B. \(\frac{ab - bc - ac}{ab}\) C. \(\frac{a^2 - b^2 + ac}{ab}\) D. \(\frac{a^2 - b^2 - ac}{ab}\) Detailed Solution\(\frac{a}{b} - \frac{b}{d} - \frac{c}{b}\)\(\frac{a^2 - b^2- ac}{ab}\) |
|
| 23. |
A. \(\frac{1}{\sqrt{3}}\) B. \(\frac{\sqrt{3}}{2}\) C. \(\sqrt{3}\) D. \(\frac{1}{2}\) Detailed Solution ZT = \(\sqrt{6^2 - 3^2}\) ZT = \(\sqrt{27}\) = \(3\sqrt{3}\) tan (< XZT) = \(\frac{3}{3\sqrt{3}}\) = - \(\frac{1}{\sqrt{3}}\) |
|
| 24. |
A fence 2.4 m tall, is 10m away from a tree of height 16m. Calculate the angle of elevation of the top of the tree from the top of the fence. A. 76.11\(^o\) B. 53.67\(^o\) C. 52.40\(^o\) D. 51.32\(^o\) Detailed Solution Tan \(\theta\) = \(\frac{13.6}{10}\) = tan\(^{-1}\)(1.36) \(\theta\) = 53.67\(^o\) |
|
| 25. |
Fati buys milk at ₦x per tin sells each at a profit of ₦y. If she sells 10 tins of milk, how much does she receives from the sales? A. ₦(xy + 10) B. ₦(x + 10y) C. ₦(10x + y) D. ₦10(x + y) Detailed SolutionSelling Price for each = ₦x + ₦y= 10(₦x + ₦y) |
|
| 26. |
If tan y is positive and sin y is negative, in which quadrant would y lie? A. First and third only B. First and second only C. Third only D. Second only |
C |
| 27. |
The dimension of a rectangular base of a right pyramid is 9 cm by 5cm. If the volume of the pyramid is 105 cm\(^3\), how high is the pyramid? A. 10cm B. 6cm C. 8cm D. 7cm Detailed SolutionVolume = \(\frac{1}{3}\) x 9 x 5 x h105 = \(\frac{1}{3}\) x 9 x 5 x h \(\frac{105}{15} = \frac{15h}{15}\) h = 7cm |
|
| 28. |
Each interior angle of a regular polygon is 168\(^o\). Find the number of sides of the polygon A. 30 B. 36 C. 24 D. 18 Detailed SolutionExterior angle = 180\(^o\) - 168\(^o\)Number of sides = \(\frac{360^o}{12}\) = 30\(^o\) |
|
| 29. |
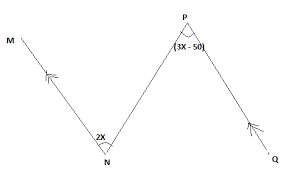 In the diagram, \(\overline{MN}\)//\(\overline{PQ}\), < MNP = 2x, and < NPQ = (3x - 50\(\^o\)). Find the value of < NPQ A. 200\(^o\) B. 150\(^o\) C. 120\(^o\) D. 90\(^o\) Detailed Solution 2x = 3x - 50 alternate angle 50\(^o\) = 3x - 2x 50\(^o\) = x < NPQ = (3x - 50)\(^o\) = 3(500)\(^o\) - 50 = 150 - 50 = 150\(^o\) |
|
| 30. |
The length of an arc of a circle of radius 3.5 cm is 1\(\frac{19}{36}\) cm. Calculate, correct to the nearest degree , the angle substended by the centre of the circle. [Take \(\pi = \frac{22}{7}\)] A. 55\(^o\) B. 36\(^o\) C. 25\(^o\) D. 22\(^o\) Detailed SolutionL = \(\frac{\theta}{360^o}\) = 2\(\pi\)\(\frac{55}{36} = \frac{\theta}{360^o} \times 2 \times \frac{22}{7} \times 3.5\) \(\theta = \frac{360 \times 55 \times 44 \times 0.5}{3 \times 44 \times 0.5}\) = \(\theta = 25^o\) |
| 21. |
A man is five times as old as his son. In four years' time, the product of their ages would be 340. If the son's age is y, express the product of their ages in terms of y. A. 5y\(^2 - 16y - 380 = 0\) B. 5y\(^2 - 24y - 380 = 0\) C. 5y\(^2 - 16y - 330 = 0\) D. 5y\(^2 - 24y - 324 = 0\) Detailed SolutionMan = x, Son = yx = 5y (x + 4)(y + 4) = 350 (5y + 4)(y + 4) = 340 5y\(^2\) + 20y + 4y + 16 - 240 = 0 5y\(^2\) + 24y - 324 = 0 |
|
| 22. |
Simplify; \(\frac{a}{b} - \frac{a}{a} - \frac{c}{b}\) A. \(\frac{a - b + c}{ab}\) B. \(\frac{ab - bc - ac}{ab}\) C. \(\frac{a^2 - b^2 + ac}{ab}\) D. \(\frac{a^2 - b^2 - ac}{ab}\) Detailed Solution\(\frac{a}{b} - \frac{b}{d} - \frac{c}{b}\)\(\frac{a^2 - b^2- ac}{ab}\) |
|
| 23. |
A. \(\frac{1}{\sqrt{3}}\) B. \(\frac{\sqrt{3}}{2}\) C. \(\sqrt{3}\) D. \(\frac{1}{2}\) Detailed Solution ZT = \(\sqrt{6^2 - 3^2}\) ZT = \(\sqrt{27}\) = \(3\sqrt{3}\) tan (< XZT) = \(\frac{3}{3\sqrt{3}}\) = - \(\frac{1}{\sqrt{3}}\) |
|
| 24. |
A fence 2.4 m tall, is 10m away from a tree of height 16m. Calculate the angle of elevation of the top of the tree from the top of the fence. A. 76.11\(^o\) B. 53.67\(^o\) C. 52.40\(^o\) D. 51.32\(^o\) Detailed Solution Tan \(\theta\) = \(\frac{13.6}{10}\) = tan\(^{-1}\)(1.36) \(\theta\) = 53.67\(^o\) |
|
| 25. |
Fati buys milk at ₦x per tin sells each at a profit of ₦y. If she sells 10 tins of milk, how much does she receives from the sales? A. ₦(xy + 10) B. ₦(x + 10y) C. ₦(10x + y) D. ₦10(x + y) Detailed SolutionSelling Price for each = ₦x + ₦y= 10(₦x + ₦y) |
| 26. |
If tan y is positive and sin y is negative, in which quadrant would y lie? A. First and third only B. First and second only C. Third only D. Second only |
C |
| 27. |
The dimension of a rectangular base of a right pyramid is 9 cm by 5cm. If the volume of the pyramid is 105 cm\(^3\), how high is the pyramid? A. 10cm B. 6cm C. 8cm D. 7cm Detailed SolutionVolume = \(\frac{1}{3}\) x 9 x 5 x h105 = \(\frac{1}{3}\) x 9 x 5 x h \(\frac{105}{15} = \frac{15h}{15}\) h = 7cm |
|
| 28. |
Each interior angle of a regular polygon is 168\(^o\). Find the number of sides of the polygon A. 30 B. 36 C. 24 D. 18 Detailed SolutionExterior angle = 180\(^o\) - 168\(^o\)Number of sides = \(\frac{360^o}{12}\) = 30\(^o\) |
|
| 29. |
 In the diagram, \(\overline{MN}\)//\(\overline{PQ}\), < MNP = 2x, and < NPQ = (3x - 50\(\^o\)). Find the value of < NPQ A. 200\(^o\) B. 150\(^o\) C. 120\(^o\) D. 90\(^o\) Detailed Solution 2x = 3x - 50 alternate angle 50\(^o\) = 3x - 2x 50\(^o\) = x < NPQ = (3x - 50)\(^o\) = 3(500)\(^o\) - 50 = 150 - 50 = 150\(^o\) |
|
| 30. |
The length of an arc of a circle of radius 3.5 cm is 1\(\frac{19}{36}\) cm. Calculate, correct to the nearest degree , the angle substended by the centre of the circle. [Take \(\pi = \frac{22}{7}\)] A. 55\(^o\) B. 36\(^o\) C. 25\(^o\) D. 22\(^o\) Detailed SolutionL = \(\frac{\theta}{360^o}\) = 2\(\pi\)\(\frac{55}{36} = \frac{\theta}{360^o} \times 2 \times \frac{22}{7} \times 3.5\) \(\theta = \frac{360 \times 55 \times 44 \times 0.5}{3 \times 44 \times 0.5}\) = \(\theta = 25^o\) |