Year :
1986
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 48 of 48 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
The table below gives the scores of a group of students in a Mathematical test. A. (27, 4) B. (14,4) C. (13,4) D. (4,4) Detailed SolutionM = mode = the number having the highest frequency = 4S = Number of students with 4 or less marks = 14 + 7 + 4 + 2 = 27 ∴ (M,S) = (27, 4) |
|
| 42. |
 In the diagram, PQ and RS are chords of a circle centre O which meet at T outside the circle. If TP = 24cm. TQ = 8cm and TS = 12cm, find TR. A. 16cm B. 14cm C. 12cm D. 8cm Detailed Solution
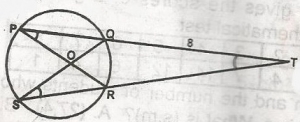 24 x 8 = TR x 12 TR = \(\frac{24 \times 8}{12}\) = = 16cm |
|
| 43. |
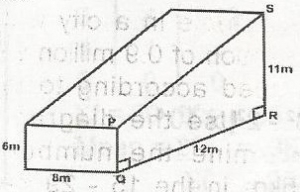 The figure is a solid with the trapezium PQRS as its uniform cross-section. Find its volume A. 120m2 B. 576m3 C. 816m3 D. 1056m3 Detailed SolutionVolume of solid = cross section x HSince the cross section is a trapezium = \(\frac{1}{2} (6 + 11) \times 12 \times 8\) = 6 x 17 x 8 = 816m3 |
|
| 44. |
 PQ and PR are tangents from P to a circle centre O as shown in the figure. If QRP = 34o, find the angle marked x A. 34o B. 56o C. 68o D. 112o Detailed SolutionFrom the circle centre 0, if PQ & PR are tangents from P and QRP = 34oThen the angle marked x i.e. QOP 34o x 2 = 68o |
|
| 45. |
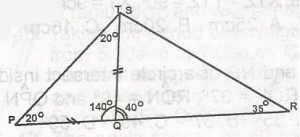
 In the figure, \(\bigtriangleup\)PQT is isosceles. PQ = QT, SRQ = 35o, TPQ = 20o and PQR is a straight line.Calculate TSR A. 20o B. 55o C. 75o D. 140o Detailed Solution
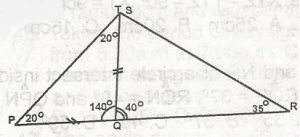 TPQ = 20o PQR = is a straight line Since PQ = QT, angle P = angle T = 20o Angle PQR = 180o - (20 + 20) = 140o TQR = 180o - 140o = 40o < on a straight line QSR = 180o - (40 + 35)& |
|
| 46. |
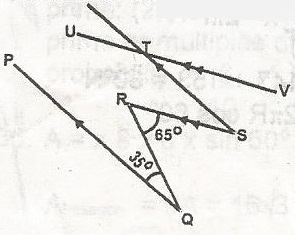 In the figure, PQ||ST, RS||UV. If PQR = 35o and QRS = 65o, find STV A. 30o B. 35o C. 55o D. 65o Detailed SolutionDraw XW//PQ and ARW = 35o (alternative angle)WRS = 60 - 30 = 30o RSR = 30o (Alternative angle) STV = 30o (Alternative angle) |
|
| 47. |
 The people in a city with a population of 0.9 million were grouped according to their ages. Use the diagram to determine the number of people in the 15 - 29 years group A. 29 x 104 B. 26 x 104 C. 16 x 104 D. 13 x 104 Detailed Solution15 - 29 years is represented by 104oNumber of people in the group is \(\frac{104}{360}\) x 0.9m = 260000 = 26 x 104 |
|
| 48. |
 In \(\bigtriangleup\)XYZ, determine the cosine of angle Z. A. \(\frac{3}{39}\) B. \(\frac{29}{36}\) C. \(\frac{14}{5}\) D. \(\frac{7}{5}\) Detailed Solution
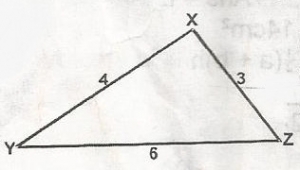 = \(\frac{9 + 36 - 16}{2(3)(6)}\) = \(\frac{29}{36}\) |
| 41. |
The table below gives the scores of a group of students in a Mathematical test. A. (27, 4) B. (14,4) C. (13,4) D. (4,4) Detailed SolutionM = mode = the number having the highest frequency = 4S = Number of students with 4 or less marks = 14 + 7 + 4 + 2 = 27 ∴ (M,S) = (27, 4) |
|
| 42. |
 In the diagram, PQ and RS are chords of a circle centre O which meet at T outside the circle. If TP = 24cm. TQ = 8cm and TS = 12cm, find TR. A. 16cm B. 14cm C. 12cm D. 8cm Detailed Solution
 24 x 8 = TR x 12 TR = \(\frac{24 \times 8}{12}\) = = 16cm |
|
| 43. |
 The figure is a solid with the trapezium PQRS as its uniform cross-section. Find its volume A. 120m2 B. 576m3 C. 816m3 D. 1056m3 Detailed SolutionVolume of solid = cross section x HSince the cross section is a trapezium = \(\frac{1}{2} (6 + 11) \times 12 \times 8\) = 6 x 17 x 8 = 816m3 |
|
| 44. |
 PQ and PR are tangents from P to a circle centre O as shown in the figure. If QRP = 34o, find the angle marked x A. 34o B. 56o C. 68o D. 112o Detailed SolutionFrom the circle centre 0, if PQ & PR are tangents from P and QRP = 34oThen the angle marked x i.e. QOP 34o x 2 = 68o |
| 45. |
 In the figure, \(\bigtriangleup\)PQT is isosceles. PQ = QT, SRQ = 35o, TPQ = 20o and PQR is a straight line.Calculate TSR A. 20o B. 55o C. 75o D. 140o Detailed Solution
 TPQ = 20o PQR = is a straight line Since PQ = QT, angle P = angle T = 20o Angle PQR = 180o - (20 + 20) = 140o TQR = 180o - 140o = 40o < on a straight line QSR = 180o - (40 + 35)& |
|
| 46. |
 In the figure, PQ||ST, RS||UV. If PQR = 35o and QRS = 65o, find STV A. 30o B. 35o C. 55o D. 65o Detailed SolutionDraw XW//PQ and ARW = 35o (alternative angle)WRS = 60 - 30 = 30o RSR = 30o (Alternative angle) STV = 30o (Alternative angle) |
|
| 47. |
 The people in a city with a population of 0.9 million were grouped according to their ages. Use the diagram to determine the number of people in the 15 - 29 years group A. 29 x 104 B. 26 x 104 C. 16 x 104 D. 13 x 104 Detailed Solution15 - 29 years is represented by 104oNumber of people in the group is \(\frac{104}{360}\) x 0.9m = 260000 = 26 x 104 |
|
| 48. |
 In \(\bigtriangleup\)XYZ, determine the cosine of angle Z. A. \(\frac{3}{39}\) B. \(\frac{29}{36}\) C. \(\frac{14}{5}\) D. \(\frac{7}{5}\) Detailed Solution
 = \(\frac{9 + 36 - 16}{2(3)(6)}\) = \(\frac{29}{36}\) |