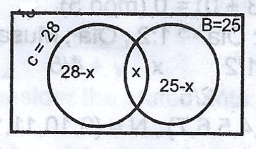Year :
2017
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
41 - 49 of 49 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
 Table:The table gives the distribution of marks obtained by a number of pupils in a class test. Using this information, Find the median of the distribution A. 4 B. 3 C. 1 D. 2 Detailed SolutionMedian is \(\frac{n}{2} = \frac{6}{2}\)= 3 Median = 3 |
|
| 42. |
 Table:The table gives the distribution of marks obtained by a number of pupils in a class test. Using this information, find the first quartile A. 1.0 B. 1.5 C. 2.0 D. 2.5 Detailed SolutionFirst quartile = \(\frac{n}{4} = \frac{60}{4}\) = 15The 15th value is 2 |
|
| 43. |
In a class of 45 students, 28 offer chemistry and 25 offer Biology. If each student offers at least one of the two subjects, calculate the probability that a student selected at random from the class the class offers chemistry only. A. \(\frac{2}{9}\) B. \(\frac{4}{9}\) C. \(\frac{5}{9}\) D. \(\frac{7}{9}\) Detailed Solution
53 - x = 45 x = 53 - 45 x = 8 chemistry only = 28 - 8 = 20 Probability = \(\frac{20}{45}\) = \(\frac{4}{9}\) |
|
| 44. |
 In the diagram, NQ//TS, <RTS = 50\(^o\) and <PRT = 100\(^o\). Find the value of <NPR A. 110\(^o\) B. 130\(^o\) C. 140\(^o\) D. 150\(^o\) Detailed Solution< TSR = 180 - (80 + 50)= 180 - (130) = 50\(^o\) < QPR = < TSR corresponding < s < NPR + QPR = < NPR 180\(^o\) - < QPR = < NPR 180\(^o\) - 50 = < NPR < NPR = 130\(^o\) |
|
| 45. |
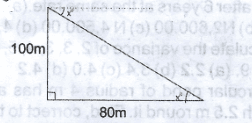
A stationary boat is observed from a height of 100m. If the horizontal distance between the observer and the boat is 80m, calculate, correct to two decimal places, the angles of depression of the boat from point of observation A. 36.87\(^o\) B. 39.70\(^o\) C. 51.34\(^o\) D. 53.13\(^o\) Detailed Solution
Tan \(x^o = Tan^{-1} 1.25\) x = 51.34\(^o\) |
|
| 46. |
The diagonal of a square is 60 cm. Calculate its peremeter A. 20\(\sqrt{2}\) B. 40\(\sqrt{2}\) C. 90\(\sqrt{2}\) D. 120\(\sqrt{2}\) Detailed Solution
\(360^2 = 2x^2\) \(x^2\) = 1800 x = \(\sqrt{1800}\) x = 42.4264 x = 42.4264 perimeter = 4x = 4 x 42.4264 = 169.7056 = 120\(\sqrt{2}\) = 120\(\sqrt{2}\) |
|
| 47. |
Find the value of m in the diagram A. 72\(^o\) B. 68\(^o\) C. 44\(^o\) D. 34\(^o\) Detailed Solution2x + m = 180x + m = 112 x = 122 - m 2(112 - m) + m = 180 224 - 2m + m = 180 224 - m = 180 224 - 180 = m m = 44\(^o\) |
|
| 48. |
 The graph of y = \(ax^2 + bx + c\) is shown oon the diagram. Find the minimum value of y A. -2, 0 B. -2, 1 C. -2, 3 D. -2, 5 |
B |
| 49. |
In the diagram, PR is a diameter of the circle RSP, RP is produced to T and TS is a tangent to the circle at S. If < PRS = 24\(^o\), calculate the value of < STR A. 24\(^o\) B. 42\(^o\) C. 48\(^o\) D. 66\(^o\) Detailed SolutionRSP = 90 < substance in semi a circleRPS = 180 - (90 + 24) = 180 - (114) = 66 TPS = 180 - 66 = 114 RST = 24 < STR = 180 - (114 + 24) = 180 - 138 = 42\(^o\) |
| 41. |
 Table:The table gives the distribution of marks obtained by a number of pupils in a class test. Using this information, Find the median of the distribution A. 4 B. 3 C. 1 D. 2 Detailed SolutionMedian is \(\frac{n}{2} = \frac{6}{2}\)= 3 Median = 3 |
|
| 42. |
 Table:The table gives the distribution of marks obtained by a number of pupils in a class test. Using this information, find the first quartile A. 1.0 B. 1.5 C. 2.0 D. 2.5 Detailed SolutionFirst quartile = \(\frac{n}{4} = \frac{60}{4}\) = 15The 15th value is 2 |
|
| 43. |
In a class of 45 students, 28 offer chemistry and 25 offer Biology. If each student offers at least one of the two subjects, calculate the probability that a student selected at random from the class the class offers chemistry only. A. \(\frac{2}{9}\) B. \(\frac{4}{9}\) C. \(\frac{5}{9}\) D. \(\frac{7}{9}\) Detailed Solution
53 - x = 45 x = 53 - 45 x = 8 chemistry only = 28 - 8 = 20 Probability = \(\frac{20}{45}\) = \(\frac{4}{9}\) |
|
| 44. |
 In the diagram, NQ//TS, <RTS = 50\(^o\) and <PRT = 100\(^o\). Find the value of <NPR A. 110\(^o\) B. 130\(^o\) C. 140\(^o\) D. 150\(^o\) Detailed Solution< TSR = 180 - (80 + 50)= 180 - (130) = 50\(^o\) < QPR = < TSR corresponding < s < NPR + QPR = < NPR 180\(^o\) - < QPR = < NPR 180\(^o\) - 50 = < NPR < NPR = 130\(^o\) |
|
| 45. |
A stationary boat is observed from a height of 100m. If the horizontal distance between the observer and the boat is 80m, calculate, correct to two decimal places, the angles of depression of the boat from point of observation A. 36.87\(^o\) B. 39.70\(^o\) C. 51.34\(^o\) D. 53.13\(^o\) Detailed Solution
Tan \(x^o = Tan^{-1} 1.25\) x = 51.34\(^o\) |
| 46. |
The diagonal of a square is 60 cm. Calculate its peremeter A. 20\(\sqrt{2}\) B. 40\(\sqrt{2}\) C. 90\(\sqrt{2}\) D. 120\(\sqrt{2}\) Detailed Solution
\(360^2 = 2x^2\) \(x^2\) = 1800 x = \(\sqrt{1800}\) x = 42.4264 x = 42.4264 perimeter = 4x = 4 x 42.4264 = 169.7056 = 120\(\sqrt{2}\) = 120\(\sqrt{2}\) |
|
| 47. |
Find the value of m in the diagram A. 72\(^o\) B. 68\(^o\) C. 44\(^o\) D. 34\(^o\) Detailed Solution2x + m = 180x + m = 112 x = 122 - m 2(112 - m) + m = 180 224 - 2m + m = 180 224 - m = 180 224 - 180 = m m = 44\(^o\) |
|
| 48. |
 The graph of y = \(ax^2 + bx + c\) is shown oon the diagram. Find the minimum value of y A. -2, 0 B. -2, 1 C. -2, 3 D. -2, 5 |
B |
| 49. |
In the diagram, PR is a diameter of the circle RSP, RP is produced to T and TS is a tangent to the circle at S. If < PRS = 24\(^o\), calculate the value of < STR A. 24\(^o\) B. 42\(^o\) C. 48\(^o\) D. 66\(^o\) Detailed SolutionRSP = 90 < substance in semi a circleRPS = 180 - (90 + 24) = 180 - (114) = 66 TPS = 180 - 66 = 114 RST = 24 < STR = 180 - (114 + 24) = 180 - 138 = 42\(^o\) |