Year :
2017
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
31 - 40 of 49 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
Given that t = \(2 ^{-x}\), find \(2 ^{x + 1}\) in terms of t. A. \(\frac{2}{t}\) B. \(\frac{t}{2}\) C. \(\frac{1}{2t}\) D. t Detailed Solutiont = \(2^{-x} = \frac{1}{2^{x}}\)\(\implies 2^{x} =\frac{1}{t}\) \(2^{x+1} = 2^{x} \times 2^{1}\) = \(\frac{1}{t} \times 2 = \frac{2}{t}\) |
|
| 32. |
Two bottles are drawn with replacement from a crate containing 8 coke, 12 and 4 sprite bottles. What is the probability that the first is coke and the second is not coke? A. \(\frac{1}{12}\) B. \(\frac{1}{6}\) C. \(\frac{2}{9}\) D. \(\frac{3}{8}\) Detailed SolutionTotal = 8 + 12 + 4= 24 \(\frac{8}{24} \times (\frac{12}{24} + \frac{4}{24}\)) = \(\frac{1}{3} \times (\frac{1}{2} + \frac{1}{6}\)) = \(\frac{1}{3} \times \frac{3 + 1}{6}\) \(\frac{1}{3} \times \frac{4}{6} = \frac{2}{9}\) |
|
| 33. |
If the simple interest on a certain amount of money saved in a bank for 5 years at 2\(\frac{1}{2}\)% annum is N500.00, calculate the total amount due after 6 years at the same rate A. N2,500.00 B. N2,600.00 C. N4,500.00 D. N4,600.00 Detailed SolutionP = \(\frac{100l}{RT} = \frac{100 \times 500}{5 \times 2.5} = \frac{50,000}{12.5}\)= 4,000 Annual interest is \(\frac{500}{5}\) = 100 for 6 year = 4,000 + 100 + 100 + 100 + 100 + 100 + 100 = N 4,600 |
|
| 34. |
Calculate the variance of 2, 3, 3, 4, 5, 5, 5, 7, 7 and 9 A. 2.2 B. 3.4 C. 4.0 D. 4.2 Detailed Solutionx = \(\frac{2 + 3 + 3 + 4 + 5 + 5+ 5+ 7 + 7 + 9}{10}\)=\(\frac{50}{10}\) = 5 Variance = \(\frac{\sum{(x - x})^2}{N}\) \(\frac{9 + 4+ 4+ 1 + 4 + 4 + 16}{10}\) = \(\frac{42}{10}\) = 4.2 |
|
| 35. |
A circular pond of radius 4m has a path of width 2.5m round it. Find, correct to two decimal places, the area of the path. [Take\(\frac{22}{7}\)] A. 7.83\(m^2\) B. 32.29\(m^2\) C. 50.29\(m^2\) D. 82.50\(m^2\) Detailed SolutionArea of path = Area of (pond+path) - Area of pondThe area of the pond with the path: The radius = (4 + 2.5)m = 6.5m Area = \(\pi \times r^{2}\) = \(\frac{22}{7} \times 6.5^{2} \approxeq 132.79m^{2}\) Area of the pond = \(\frac{22}{7} \times 4^{2} \approxeq 50.29m^{2}\) Area of the path = (132.79 - 50.29)m^{2} = 82.50m^{2}\) |
|
| 36. |
 Fig. 1 and Fig. 2 are the addition and multiplication tables respectively in modulo 5. Use these tables to solve the equation (n \(\oplus 4\)) A. 1 B. 2 C. 3 D. 4 Detailed Solution(n \(\oplus\) 4) \(\oplus\) 3 = 0 (mod 5)(3 \(\oplus\) 4) \(\oplus\) 3 12 \(\oplus\) 3 = 15 (mod 5) (5 x 3 + 0) = 0 (mod 5) |
|
| 37. |
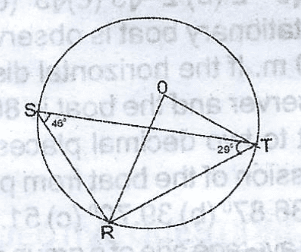 The diagram shows a circle centre O. if A. 12\(^o\) B. 15\(^o\) C. 29\(^o\) D. 34\(^o\) Detailed SolutionSRT = 180 - (46 + 29) sum of < s in a= 180 - 75 = 105 SOT = 2 x 46 < at the centre is twice all the circle = 92 RTO = 180 - (96 + 43) = 41 STO = 41 - 29 = 12\(^o\) |
|
| 38. |
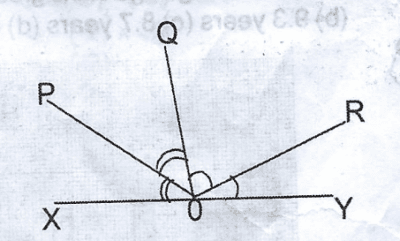 In the diagram, XY is a straight line. <POX = <POQ and <ROY = <QOR. Find the value of <POQ + <ROY. A. 60\(^o\) B. 90\(^o\) C. 100\(^o\) D. 120\(^o\) Detailed Solution<POX = <POQ; <ROY = QOR2 <POQ + 2 <ROY = 180 2(<POQ = <ROY) = 180 <POQ + <ROY = 90 |
|
| 39. |
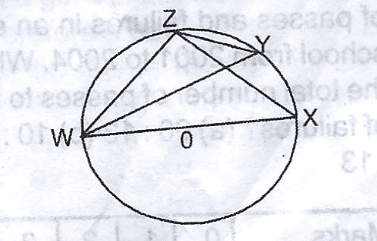 The diagram shows a circle O. If < ZYW = 33\(^o\) , find < ZWX A. 33\(^o\) B. 57\(^o\) C. 90\(^o\) D. 100\(^o\) Detailed SolutionIn ZY = 90\(^o\) < subtends In a semi OZWY = 180 - (90\(^o\) + 33) = 57 ZWX = 57 + 33 = 90\(^o\) |
|
| 40. |
 In the diagram, PQ and PS are tangents to the circle O. If PSQ = m, <SPQ = n and <SQR = 33\(^o\), find the value of (m + n) A. 103\(^o\) B. 123\(^o\) C. 133\(^o\) D. 143\(^o\) Detailed Solution< SQP = 180 - (90 + 33) < on a ----= 180 - (123) = 57\(^o\) Therefore, (m + n) = 123\(^o\) |
| 31. |
Given that t = \(2 ^{-x}\), find \(2 ^{x + 1}\) in terms of t. A. \(\frac{2}{t}\) B. \(\frac{t}{2}\) C. \(\frac{1}{2t}\) D. t Detailed Solutiont = \(2^{-x} = \frac{1}{2^{x}}\)\(\implies 2^{x} =\frac{1}{t}\) \(2^{x+1} = 2^{x} \times 2^{1}\) = \(\frac{1}{t} \times 2 = \frac{2}{t}\) |
|
| 32. |
Two bottles are drawn with replacement from a crate containing 8 coke, 12 and 4 sprite bottles. What is the probability that the first is coke and the second is not coke? A. \(\frac{1}{12}\) B. \(\frac{1}{6}\) C. \(\frac{2}{9}\) D. \(\frac{3}{8}\) Detailed SolutionTotal = 8 + 12 + 4= 24 \(\frac{8}{24} \times (\frac{12}{24} + \frac{4}{24}\)) = \(\frac{1}{3} \times (\frac{1}{2} + \frac{1}{6}\)) = \(\frac{1}{3} \times \frac{3 + 1}{6}\) \(\frac{1}{3} \times \frac{4}{6} = \frac{2}{9}\) |
|
| 33. |
If the simple interest on a certain amount of money saved in a bank for 5 years at 2\(\frac{1}{2}\)% annum is N500.00, calculate the total amount due after 6 years at the same rate A. N2,500.00 B. N2,600.00 C. N4,500.00 D. N4,600.00 Detailed SolutionP = \(\frac{100l}{RT} = \frac{100 \times 500}{5 \times 2.5} = \frac{50,000}{12.5}\)= 4,000 Annual interest is \(\frac{500}{5}\) = 100 for 6 year = 4,000 + 100 + 100 + 100 + 100 + 100 + 100 = N 4,600 |
|
| 34. |
Calculate the variance of 2, 3, 3, 4, 5, 5, 5, 7, 7 and 9 A. 2.2 B. 3.4 C. 4.0 D. 4.2 Detailed Solutionx = \(\frac{2 + 3 + 3 + 4 + 5 + 5+ 5+ 7 + 7 + 9}{10}\)=\(\frac{50}{10}\) = 5 Variance = \(\frac{\sum{(x - x})^2}{N}\) \(\frac{9 + 4+ 4+ 1 + 4 + 4 + 16}{10}\) = \(\frac{42}{10}\) = 4.2 |
|
| 35. |
A circular pond of radius 4m has a path of width 2.5m round it. Find, correct to two decimal places, the area of the path. [Take\(\frac{22}{7}\)] A. 7.83\(m^2\) B. 32.29\(m^2\) C. 50.29\(m^2\) D. 82.50\(m^2\) Detailed SolutionArea of path = Area of (pond+path) - Area of pondThe area of the pond with the path: The radius = (4 + 2.5)m = 6.5m Area = \(\pi \times r^{2}\) = \(\frac{22}{7} \times 6.5^{2} \approxeq 132.79m^{2}\) Area of the pond = \(\frac{22}{7} \times 4^{2} \approxeq 50.29m^{2}\) Area of the path = (132.79 - 50.29)m^{2} = 82.50m^{2}\) |
| 36. |
 Fig. 1 and Fig. 2 are the addition and multiplication tables respectively in modulo 5. Use these tables to solve the equation (n \(\oplus 4\)) A. 1 B. 2 C. 3 D. 4 Detailed Solution(n \(\oplus\) 4) \(\oplus\) 3 = 0 (mod 5)(3 \(\oplus\) 4) \(\oplus\) 3 12 \(\oplus\) 3 = 15 (mod 5) (5 x 3 + 0) = 0 (mod 5) |
|
| 37. |
 The diagram shows a circle centre O. if A. 12\(^o\) B. 15\(^o\) C. 29\(^o\) D. 34\(^o\) Detailed SolutionSRT = 180 - (46 + 29) sum of < s in a= 180 - 75 = 105 SOT = 2 x 46 < at the centre is twice all the circle = 92 RTO = 180 - (96 + 43) = 41 STO = 41 - 29 = 12\(^o\) |
|
| 38. |
 In the diagram, XY is a straight line. <POX = <POQ and <ROY = <QOR. Find the value of <POQ + <ROY. A. 60\(^o\) B. 90\(^o\) C. 100\(^o\) D. 120\(^o\) Detailed Solution<POX = <POQ; <ROY = QOR2 <POQ + 2 <ROY = 180 2(<POQ = <ROY) = 180 <POQ + <ROY = 90 |
|
| 39. |
 The diagram shows a circle O. If < ZYW = 33\(^o\) , find < ZWX A. 33\(^o\) B. 57\(^o\) C. 90\(^o\) D. 100\(^o\) Detailed SolutionIn ZY = 90\(^o\) < subtends In a semi OZWY = 180 - (90\(^o\) + 33) = 57 ZWX = 57 + 33 = 90\(^o\) |
|
| 40. |
 In the diagram, PQ and PS are tangents to the circle O. If PSQ = m, <SPQ = n and <SQR = 33\(^o\), find the value of (m + n) A. 103\(^o\) B. 123\(^o\) C. 133\(^o\) D. 143\(^o\) Detailed Solution< SQP = 180 - (90 + 33) < on a ----= 180 - (123) = 57\(^o\) Therefore, (m + n) = 123\(^o\) |