Year :
2012
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
31 - 40 of 48 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
Evaluate \(\int^{\frac{\pi}{4}}_0sec^2 \theta d \theta\) A. 1 B. 2 C. 3 D. 4 Detailed Solution\(\int^{\frac{\pi}{4}}_0sec^2 \theta d \theta\)= \([\tan \theta]_{0} ^{\frac{\pi}{4}}\) = \(\tan \frac{\pi}{4} - \tan 0\) = \(1 - 0\) = 1. There is an explanation video available below. |
|
| 32. |
The mean of seven numbers is 96. If an eighth number is added, the mean becomes 112. Find the eighth number. A. 126 B. 180 C. 216 D. 224 Detailed Solution\(\frac{x}{7} = \frac{96}{1}\) ==> \(\frac{672 + x}{8} = 112\)Therefore x = 224 |
|
| 33. |
Find the median of 2,3,7,3,4,5,8,9,9,4,5,3,4,2,4 and 5 A. 9 B. 8 C. 7 D. 4 |
|
| 34. |
Find the range of 4,9,6,3,2,8,10 and 11 A. 11 B. 9 C. 8 D. 4 |
|
| 35. |
Find the standard deviation of 2,3,8,10 and 12 A. 3.9 B. 4.9 C. 5.9 D. 6.9 |
|
| 36. |
Evaluate n+1Cn-2 If n =15 A. 3630 B. 3360 C. 1120 D. 560 |
|
| 37. |
In how many ways can the letters of the word TOTALITY be arranged? A. 6720 B. 6270 C. 6207 D. 6027 |
|
| 38. |
The probability that a student passes a physics test is \(\frac{2}{3}\). If he takes three physics tests, what is the probability that he passes two of the tests? A. \(\frac{2}{27}\) B. \(\frac{3}{27}\) C. \(\frac{4}{27}\) D. \(\frac{5}{3}\) |
|
| 39. |
The probabilities that a man and his wife live for 80 years are \(\frac{2}{3}\) and \(\frac{3}{5}\) respectively. Find the probability that at least one of them will live up to 80 years A. \(\frac{2}{15}\) B. \(\frac{3}{15}\) C. \(\frac{7}{15}\) D. \(\frac{13}{15}\) Detailed SolutionMan lives = \(\frac{2}{3}\) not live = \(\frac{1}{3}\)Wife lives = \(\frac{3}{5}\) not live = \(\frac{2}{5}\) P(at least one lives to 80 years) = P(man lives to 80 not woman) + P(woman lives to 80 and not man) + P(both live to 80) \(P = (\frac{2}{3} \times \frac{2}{5}) + (\frac{2}{5} \times \frac{1}{3}) + (\frac{2}{3} \times \frac{3}{5})\) = \(\frac{4}{15} + \frac{3}{15} + \frac{6}{15}\) = \(\frac{13}{15}\) There is an explanation video available below. |
|
| 40. |
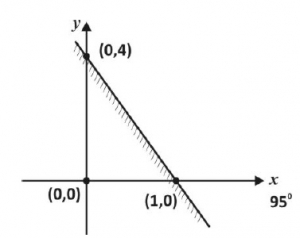 The shaded region above is represented by A. y ≤ 4x + 2 B. y ≥ 4x + 2 C. y ≤ -4x + 4 D. y ≤ 4x + 4 Detailed SolutionEquation of the line\(\frac{y - 4}{x - 0} = \frac{0 - 4}{1 - 0}\) \(\frac{y - 4}{x} = \frac{-4}{1}\) \(\therefore -4x = y - 4\) \(y = -4x + 4\) \(\therefore \text{The shaded portion = } y \leq -4x + 4\) There is an explanation video available below. |
| 31. |
Evaluate \(\int^{\frac{\pi}{4}}_0sec^2 \theta d \theta\) A. 1 B. 2 C. 3 D. 4 Detailed Solution\(\int^{\frac{\pi}{4}}_0sec^2 \theta d \theta\)= \([\tan \theta]_{0} ^{\frac{\pi}{4}}\) = \(\tan \frac{\pi}{4} - \tan 0\) = \(1 - 0\) = 1. There is an explanation video available below. |
|
| 32. |
The mean of seven numbers is 96. If an eighth number is added, the mean becomes 112. Find the eighth number. A. 126 B. 180 C. 216 D. 224 Detailed Solution\(\frac{x}{7} = \frac{96}{1}\) ==> \(\frac{672 + x}{8} = 112\)Therefore x = 224 |
|
| 33. |
Find the median of 2,3,7,3,4,5,8,9,9,4,5,3,4,2,4 and 5 A. 9 B. 8 C. 7 D. 4 |
|
| 34. |
Find the range of 4,9,6,3,2,8,10 and 11 A. 11 B. 9 C. 8 D. 4 |
|
| 35. |
Find the standard deviation of 2,3,8,10 and 12 A. 3.9 B. 4.9 C. 5.9 D. 6.9 |
| 36. |
Evaluate n+1Cn-2 If n =15 A. 3630 B. 3360 C. 1120 D. 560 |
|
| 37. |
In how many ways can the letters of the word TOTALITY be arranged? A. 6720 B. 6270 C. 6207 D. 6027 |
|
| 38. |
The probability that a student passes a physics test is \(\frac{2}{3}\). If he takes three physics tests, what is the probability that he passes two of the tests? A. \(\frac{2}{27}\) B. \(\frac{3}{27}\) C. \(\frac{4}{27}\) D. \(\frac{5}{3}\) |
|
| 39. |
The probabilities that a man and his wife live for 80 years are \(\frac{2}{3}\) and \(\frac{3}{5}\) respectively. Find the probability that at least one of them will live up to 80 years A. \(\frac{2}{15}\) B. \(\frac{3}{15}\) C. \(\frac{7}{15}\) D. \(\frac{13}{15}\) Detailed SolutionMan lives = \(\frac{2}{3}\) not live = \(\frac{1}{3}\)Wife lives = \(\frac{3}{5}\) not live = \(\frac{2}{5}\) P(at least one lives to 80 years) = P(man lives to 80 not woman) + P(woman lives to 80 and not man) + P(both live to 80) \(P = (\frac{2}{3} \times \frac{2}{5}) + (\frac{2}{5} \times \frac{1}{3}) + (\frac{2}{3} \times \frac{3}{5})\) = \(\frac{4}{15} + \frac{3}{15} + \frac{6}{15}\) = \(\frac{13}{15}\) There is an explanation video available below. |
|
| 40. |
 The shaded region above is represented by A. y ≤ 4x + 2 B. y ≥ 4x + 2 C. y ≤ -4x + 4 D. y ≤ 4x + 4 Detailed SolutionEquation of the line\(\frac{y - 4}{x - 0} = \frac{0 - 4}{1 - 0}\) \(\frac{y - 4}{x} = \frac{-4}{1}\) \(\therefore -4x = y - 4\) \(y = -4x + 4\) \(\therefore \text{The shaded portion = } y \leq -4x + 4\) There is an explanation video available below. |