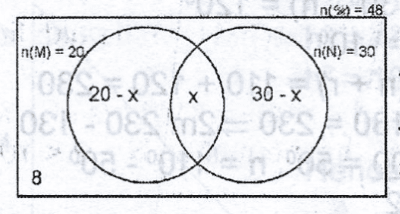Year : 
2018
Title : 
Mathematics (Core)
Exam : 
WASSCE/WAEC MAY/JUNE

Paper 1 | Objectives

41 - 50 of 50 Questions

# Question Ans
41.

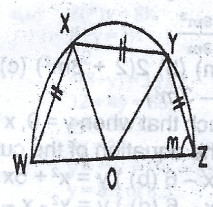The diagram shows a trapezium inscribed in a semi-circle. If O is the mid-point of WZ and |WX| = |XY| = |YZ|, calculate the value of m

A. 90\(^o\)

B. 60\(^o\)

C. 45\(^o\)

D. 30\(^o\)

Detailed Solution

In the diagram, < WOZ = 180\(^o\) (angle on a straight line)
< WOX = < XOY = < YOZ
(|WX| = |XY| = |YZ|)
\(\frac{180^o}{3}\) = 60\(^o\)
= 60\(^o\)
M + m =2m (base angles of isosceles \(\bigtriangleup\), |OY| and |OZ| are radii)
< YOZ + 2m (base angles of a \(\bigtriangleup\))
60\(^o\) + 2m = 180\(^o\) (sum of a \(\bigtriangleup\))
60\(^o\) + 2m = 180\(^o\)
2m = 180\(^o\) - 60\(^o\)
2m = 120\(^o\)
m = \(\frac{120^o}{2}\)
= 60\(^o\)
42.

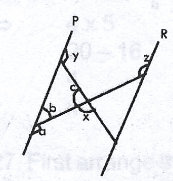
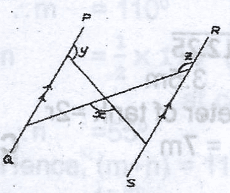In the diagram, PQ//RS. Find x in terms of y and z

A. x = 240\(^o\) - y - z

B. x = 180\(^o\) - y - z

C. x = 360\(^o\) + y -z

D. x = 360\(^o\) - y - z

Detailed Solution

In the diagram,
a = z (alternate angles)
b = 180\(^o\) - a (angles on a straight line)
b = 180\(^o\) - z
c = 180\(^o\) - x (angles on a straight line)
y = b + c (sum of oposite interior angles)
y = 180\(^o\) - z + 180\(^o\) - x
y = 360\(^o\) - z - x
x = 360\(^o\) - y - z
43.

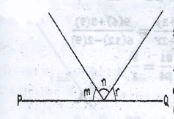In the diagram, PQ is a straight line, (m + n) = 110\(^o\) and (n + r) = 130\(^o\) and (m + r) = 120\(^o\). Find the ratio of m : n : r

A. 2 : 3 : 4

B. 3 : 4 : 5

C. 4 : 5 : 6

D. 5 : 6 : 7

Detailed Solution

m + n = 110\(^o\), (n + r) = 130\(^o\)
(m + n) = 120\(^o\)
then, r = 130\(^o\) - n
and;
m + (130^o - n) = 120\(^o\)
m - n = -10\(^o\)
2m + (n + r) = 110 + 120 = 230
2m + 130 = 230
2m = 230 - 130
m = \(\frac{100}{2}\) = 50\(^o\)
n = 110\(^o\) - 50\(^o\)
= 60\(^o\)
r = 130\(^o\) - 60\(^o\) = 70\(^o\)
Hence, the ratio m : n : r
= 50 : 60 : 70
= 5 : 6 : 7
44.

Donations during the launching of a church project were sent in sealed envolopes. The table shows the distribution of the amount of money in the envelope. How much was the donation?

A. N26,792.00

B. N26,972.00

C. N62.792.00

D. N62,972.00

Detailed Solution

Total donation = 4 x 500 + 7 x 2000 + 20 x 1000 + 9 x 700 + 4 x 500 + 5 x 100 + 3 x 50 + 1 x 2 + 2 x 10
= 20000 + 14000 + 20000 + 6300 + 2000 + 500 + 150 + 2 + 20
= N62,972
45.

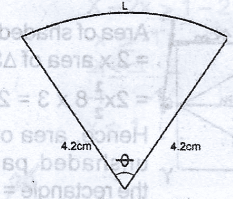
A piece of thread of length 21.4cm is used to form a sector of a circle of radius 4.2cm on a piece of cloth. Calculate, correct to the nearest degree, the angle of the sector. [Take \(\pi = \frac{22}{7}\)]

A. 170\(^o\)

B. 192\(^o\)

C. 177\(^o\)

D. 182\(^o\)

Detailed Solution

Length of arc, L = 21.4 - 2 x 4.2cm
= 21.4 - 8.4
= 13cm
But L = \(\frac{\theta}{360^o}\) x 2\(\pi r\)
i.e 13 = \(\frac{\theta}{360^o}\) x 2 x \(\frac{22}{7}\) x 4.2
= 13 x 360\(^o\) x 7
= \(\theta\) x 2 x 22 x 4.2
\(\theta\) = \(\frac{13 \times 360^o \times 7}{44 \times 4.2}\)
= \(\approx\) 177.27\(^o\)
\(\approx\) 177\(^o\) (to the nearest degree)
46.

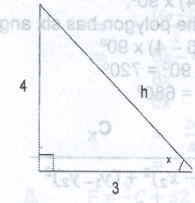
If tan x = \(\frac{4}{3}\), 0\(^o\) < x < 90\(^o\), find the value of sin x - cos x

A. \(\frac{1}{10}\)

B. \(\frac{1}{5}\)

C. \(\frac{5}{12}\)

D. 1\(\frac{2}{5}\)

Detailed Solution

From the diagram,
h\(^2\) = 4\(^2\) + 3\(^2\) (pythagoras')
h\(^2\) = 16 + 9 = 25
h = \(\sqrt{25}\) = 5
Hence, sin x - cos x
= \(\frac{4}{5} - \frac{3}{5}\)
= \(\frac{2}{5}\)
47.

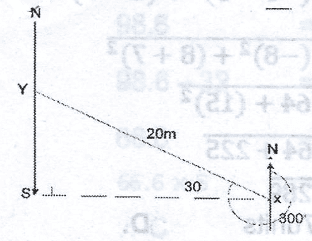
Given that Y is 20cm on a bearing of 300\(^o\) from x, how far south of y is x?

A. 10cm

B. 15cm

C. 25cm

D. 30cm

Detailed Solution

In \(\bigtriangleup\)YSC, sin 30\(^o\) = \(\frac{YS}{20}\)
|YS| = 20 sin 30\(^o\)
= 20 x 0.5
10m
48.

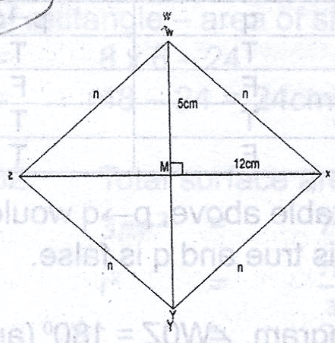
The diagonals of a rhombus WXYZ intersect at M. If |MW| = 5cm and |MX| = 12cm, calculate its perimeter

A. 42cm

B. 48cm

C. 52cm

D. 60cm

Detailed Solution

Let the length of a side of the rhombus be n
Then, n\(^2\) = 5\(^2\) + 12\(^2\)
= 25 + 144 = 169
n = \(\sqrt{169}\)
= 13cm
Hence, perimeter of rhombus = 4n = 4 x 13
= 52cm
49.

M and N are two subsets of the universal set (U). If n(U) = 48, n(M) = 20, n(N) = 30 and n(MUN) = 40, find n(M \(\cap\) N)

A. 18

B. 20

C. 30

D. 38

Detailed Solution

Let n(M \(\cup\) N \) = x
Then 20 - x + x + 30
- x = n(M \(\cup\) N)
50 - x = 40
50 - 40 = x
10 = x
x = 10
Hence, n(M \(\cup\N)' = 8 + (20 - 10) + (30 + 10)
= 8 + 10 + 20
= 38
50.

The graph of y = x\(^2\) and y = x intersect at which of these points?

A. (0,0), (1,1)

B. (0,0), (0,1)

C. (1, 0), (0, 0)

D. (0, 0) (0, 0)

Detailed Solution

y = x\(^2\) ....(1)
y = x ......(2)
y = y
x\(^2\) - x
x\(^2\) - x = 0
x(x - 1) = 0
x = 0 or x - 1 = 0
x = 0 or x = 1
when x = 0, y = 0\(^2\) = 0
when x = 1, y = 1\(^2\) = 1
Hence; the two graphs interest at (0, 0) and (1, 1)
41.

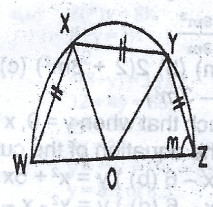The diagram shows a trapezium inscribed in a semi-circle. If O is the mid-point of WZ and |WX| = |XY| = |YZ|, calculate the value of m

A. 90\(^o\)

B. 60\(^o\)

C. 45\(^o\)

D. 30\(^o\)

Detailed Solution

In the diagram, < WOZ = 180\(^o\) (angle on a straight line)
< WOX = < XOY = < YOZ
(|WX| = |XY| = |YZ|)
\(\frac{180^o}{3}\) = 60\(^o\)
= 60\(^o\)
M + m =2m (base angles of isosceles \(\bigtriangleup\), |OY| and |OZ| are radii)
< YOZ + 2m (base angles of a \(\bigtriangleup\))
60\(^o\) + 2m = 180\(^o\) (sum of a \(\bigtriangleup\))
60\(^o\) + 2m = 180\(^o\)
2m = 180\(^o\) - 60\(^o\)
2m = 120\(^o\)
m = \(\frac{120^o}{2}\)
= 60\(^o\)
42.

In the diagram, PQ//RS. Find x in terms of y and z

A. x = 240\(^o\) - y - z

B. x = 180\(^o\) - y - z

C. x = 360\(^o\) + y -z

D. x = 360\(^o\) - y - z

Detailed Solution

In the diagram,
a = z (alternate angles)
b = 180\(^o\) - a (angles on a straight line)
b = 180\(^o\) - z
c = 180\(^o\) - x (angles on a straight line)
y = b + c (sum of oposite interior angles)
y = 180\(^o\) - z + 180\(^o\) - x
y = 360\(^o\) - z - x
x = 360\(^o\) - y - z
43.

In the diagram, PQ is a straight line, (m + n) = 110\(^o\) and (n + r) = 130\(^o\) and (m + r) = 120\(^o\). Find the ratio of m : n : r

A. 2 : 3 : 4

B. 3 : 4 : 5

C. 4 : 5 : 6

D. 5 : 6 : 7

Detailed Solution

m + n = 110\(^o\), (n + r) = 130\(^o\)
(m + n) = 120\(^o\)
then, r = 130\(^o\) - n
and;
m + (130^o - n) = 120\(^o\)
m - n = -10\(^o\)
2m + (n + r) = 110 + 120 = 230
2m + 130 = 230
2m = 230 - 130
m = \(\frac{100}{2}\) = 50\(^o\)
n = 110\(^o\) - 50\(^o\)
= 60\(^o\)
r = 130\(^o\) - 60\(^o\) = 70\(^o\)
Hence, the ratio m : n : r
= 50 : 60 : 70
= 5 : 6 : 7
44.

Donations during the launching of a church project were sent in sealed envolopes. The table shows the distribution of the amount of money in the envelope. How much was the donation?

A. N26,792.00

B. N26,972.00

C. N62.792.00

D. N62,972.00

Detailed Solution

Total donation = 4 x 500 + 7 x 2000 + 20 x 1000 + 9 x 700 + 4 x 500 + 5 x 100 + 3 x 50 + 1 x 2 + 2 x 10
= 20000 + 14000 + 20000 + 6300 + 2000 + 500 + 150 + 2 + 20
= N62,972
45.

A piece of thread of length 21.4cm is used to form a sector of a circle of radius 4.2cm on a piece of cloth. Calculate, correct to the nearest degree, the angle of the sector. [Take \(\pi = \frac{22}{7}\)]

A. 170\(^o\)

B. 192\(^o\)

C. 177\(^o\)

D. 182\(^o\)

Detailed Solution

Length of arc, L = 21.4 - 2 x 4.2cm
= 21.4 - 8.4
= 13cm
But L = \(\frac{\theta}{360^o}\) x 2\(\pi r\)
i.e 13 = \(\frac{\theta}{360^o}\) x 2 x \(\frac{22}{7}\) x 4.2
= 13 x 360\(^o\) x 7
= \(\theta\) x 2 x 22 x 4.2
\(\theta\) = \(\frac{13 \times 360^o \times 7}{44 \times 4.2}\)
= \(\approx\) 177.27\(^o\)
\(\approx\) 177\(^o\) (to the nearest degree)
46.

If tan x = \(\frac{4}{3}\), 0\(^o\) < x < 90\(^o\), find the value of sin x - cos x

A. \(\frac{1}{10}\)

B. \(\frac{1}{5}\)

C. \(\frac{5}{12}\)

D. 1\(\frac{2}{5}\)

Detailed Solution

From the diagram,
h\(^2\) = 4\(^2\) + 3\(^2\) (pythagoras')
h\(^2\) = 16 + 9 = 25
h = \(\sqrt{25}\) = 5
Hence, sin x - cos x
= \(\frac{4}{5} - \frac{3}{5}\)
= \(\frac{2}{5}\)
47.

Given that Y is 20cm on a bearing of 300\(^o\) from x, how far south of y is x?

A. 10cm

B. 15cm

C. 25cm

D. 30cm

Detailed Solution

In \(\bigtriangleup\)YSC, sin 30\(^o\) = \(\frac{YS}{20}\)
|YS| = 20 sin 30\(^o\)
= 20 x 0.5
10m
48.

The diagonals of a rhombus WXYZ intersect at M. If |MW| = 5cm and |MX| = 12cm, calculate its perimeter

A. 42cm

B. 48cm

C. 52cm

D. 60cm

Detailed Solution

Let the length of a side of the rhombus be n
Then, n\(^2\) = 5\(^2\) + 12\(^2\)
= 25 + 144 = 169
n = \(\sqrt{169}\)
= 13cm
Hence, perimeter of rhombus = 4n = 4 x 13
= 52cm
49.

M and N are two subsets of the universal set (U). If n(U) = 48, n(M) = 20, n(N) = 30 and n(MUN) = 40, find n(M \(\cap\) N)

A. 18

B. 20

C. 30

D. 38

Detailed Solution

Let n(M \(\cup\) N \) = x
Then 20 - x + x + 30
- x = n(M \(\cup\) N)
50 - x = 40
50 - 40 = x
10 = x
x = 10
Hence, n(M \(\cup\N)' = 8 + (20 - 10) + (30 + 10)
= 8 + 10 + 20
= 38
50.

The graph of y = x\(^2\) and y = x intersect at which of these points?

A. (0,0), (1,1)

B. (0,0), (0,1)

C. (1, 0), (0, 0)

D. (0, 0) (0, 0)

Detailed Solution

y = x\(^2\) ....(1)
y = x ......(2)
y = y
x\(^2\) - x
x\(^2\) - x = 0
x(x - 1) = 0
x = 0 or x - 1 = 0
x = 0 or x = 1
when x = 0, y = 0\(^2\) = 0
when x = 1, y = 1\(^2\) = 1
Hence; the two graphs interest at (0, 0) and (1, 1)