Year :
2018
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
31 - 40 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
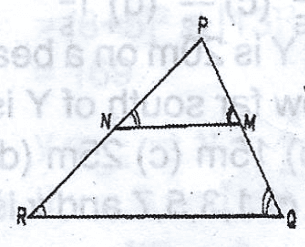 In the diagram, which of the following ratios is equal to \(\frac{|PN|}{|PQ|}\)? A. \(\frac{|PN|}{|PR|}\) B. \(\frac{|PM|}{|PQ|}\) C. \(\frac{|PM|}{|PR|}\) D. \(\frac{|PR|}{|PQ|}\) Detailed Solution\(\frac{|PN|}{|PQ|}\) = \(\frac{|PM|}{|PR|}\) |
|
| 32. |
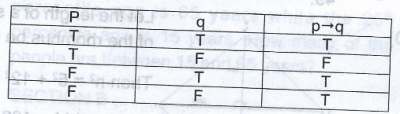
If P and Q are two statements, under what condition would p|q be false? A. If p is true and q is true B. If p is true and q is false C. If p is false and q is false D. If p is false and q is true Detailed Solution
|
|
| 33. |
Find the median of 2, 1, 0, 3, 1, 1, 4, 0, 1 and 2 A. 0.0 B. 0.5 C. 1.0 D. 1.5 Detailed SolutionFirst arrange the numbers in ascending order of magnitude; 0, 0, 1, 1, 1, 1, 2, 2, 3, 4Counting from the right, the fifth number is 1 Counting from the left, the fifth number is 1 Hence, median = \(frac{1 + 1}{2}\) = \(\frac{2}{2}\) = 1 |
|
| 34. |
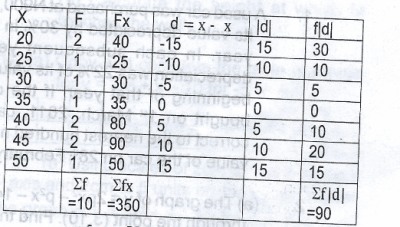
Find the mean deviation of 20, 30, 25, 40, 35, 50, 45, 40, 20 and 45 A. 8 B. 9 C. 10 D. 12 Detailed Solution
= \(\frac{350}{10}\) = 35 = \(\frac{\sum f |d|}{\sum f}\) = \(\frac{90}{10}\) = 9 |
|
| 35. |
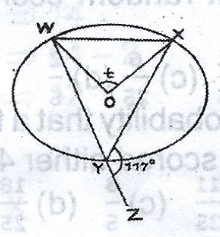
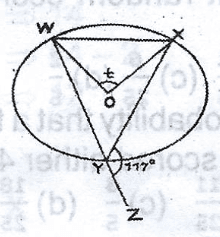 Find the value of t in the diagram A. 63\(^o\) B. 117\(^o\) C. 126\(^o\) D. 234\(^o\) Detailed Solution
\(\alpha\) = 180\(^o\) - 177\(^o\) (angles on a straight line) \(\alpha\) = 63\(^o\) t = 2 x 63\(^o\) (angle at centre = 2 x angle at circum) = 126\(^o\) |
|
| 36. |
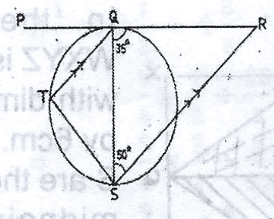
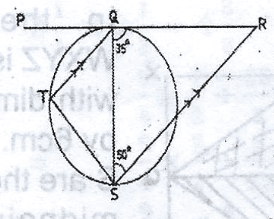 In the diagram, PR is a tangent to the circle at Q, QT//RS, A. 40\(^o\) B. 65\(^o\) C. 85\(^o\) D. 95\(^o\) Detailed Solution
a = 50\(^o\) (alternate angles) b\(_1\) + a 35\(^o\) = 180\(^o\) (sum of angles on a straight line) i.e; b\(_1\) + 50\(^o\) + 35\(^o\) = 180v b\(_1\) + 180\(^o\) - 85\(^o\) = 90\(^o\) But b\(_2\) = \(b_1\) = 95\(^o\) (angles in alternate segement) <QST = b\(_2\) = 95\(^o\) |
|
| 37. |
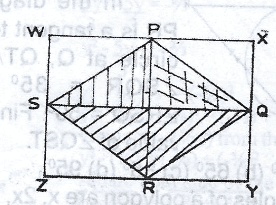 In the diagram, WXYZ is a rectangle with dimension 8cm by 6cm. P, Q, R and S are the midpoints of the sides of the rectangle as shown. Using this information, what type of quadrilateral is the shaded region? A. Trapezium B. Prism C. Rectangle D. Rhombus |
D |
| 38. |
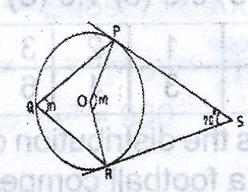 In the diagram, PS and RS are tangents to the circle centre O, A. 110\(^o\) B. 135\(^o\) C. 165\(^o\) D. 225\(^o\) |
|
| 39. |
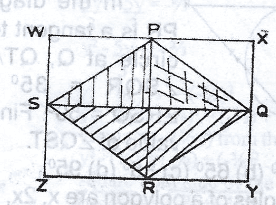 In the diagram, WXYZ is a rectangle with diamension 8cm by 6cm. P, Q, R and S are the midpoints of the rectangle as shown. Using this information calculate the area of the part of the rectangle that is not shaded A. 25cm\(^2\) B. 24cm\(^2\) C. 16cm\(^2\) D. 12cm\(^2\) |
|
| 40. |
 The solution of x + 2 \(\geq\) 2x + 1 is illustrated A. i B. ii C. iii D. iv Detailed Solutionx + 2 \(\geq\) 2x + 1x - 2x \(\geq\) 1 - 2 -x \(\geq\) -1 \(\frac{-x}{-1}\) \(\geq\) \(\frac{-1}{-1}\) x \(\leq\) 1 |
| 31. |
 In the diagram, which of the following ratios is equal to \(\frac{|PN|}{|PQ|}\)? A. \(\frac{|PN|}{|PR|}\) B. \(\frac{|PM|}{|PQ|}\) C. \(\frac{|PM|}{|PR|}\) D. \(\frac{|PR|}{|PQ|}\) Detailed Solution\(\frac{|PN|}{|PQ|}\) = \(\frac{|PM|}{|PR|}\) |
|
| 32. |
If P and Q are two statements, under what condition would p|q be false? A. If p is true and q is true B. If p is true and q is false C. If p is false and q is false D. If p is false and q is true Detailed Solution
|
|
| 33. |
Find the median of 2, 1, 0, 3, 1, 1, 4, 0, 1 and 2 A. 0.0 B. 0.5 C. 1.0 D. 1.5 Detailed SolutionFirst arrange the numbers in ascending order of magnitude; 0, 0, 1, 1, 1, 1, 2, 2, 3, 4Counting from the right, the fifth number is 1 Counting from the left, the fifth number is 1 Hence, median = \(frac{1 + 1}{2}\) = \(\frac{2}{2}\) = 1 |
|
| 34. |
Find the mean deviation of 20, 30, 25, 40, 35, 50, 45, 40, 20 and 45 A. 8 B. 9 C. 10 D. 12 Detailed Solution
= \(\frac{350}{10}\) = 35 = \(\frac{\sum f |d|}{\sum f}\) = \(\frac{90}{10}\) = 9 |
|
| 35. |
 Find the value of t in the diagram A. 63\(^o\) B. 117\(^o\) C. 126\(^o\) D. 234\(^o\) Detailed Solution
\(\alpha\) = 180\(^o\) - 177\(^o\) (angles on a straight line) \(\alpha\) = 63\(^o\) t = 2 x 63\(^o\) (angle at centre = 2 x angle at circum) = 126\(^o\) |
| 36. |
 In the diagram, PR is a tangent to the circle at Q, QT//RS, A. 40\(^o\) B. 65\(^o\) C. 85\(^o\) D. 95\(^o\) Detailed Solution
a = 50\(^o\) (alternate angles) b\(_1\) + a 35\(^o\) = 180\(^o\) (sum of angles on a straight line) i.e; b\(_1\) + 50\(^o\) + 35\(^o\) = 180v b\(_1\) + 180\(^o\) - 85\(^o\) = 90\(^o\) But b\(_2\) = \(b_1\) = 95\(^o\) (angles in alternate segement) <QST = b\(_2\) = 95\(^o\) |
|
| 37. |
 In the diagram, WXYZ is a rectangle with dimension 8cm by 6cm. P, Q, R and S are the midpoints of the sides of the rectangle as shown. Using this information, what type of quadrilateral is the shaded region? A. Trapezium B. Prism C. Rectangle D. Rhombus |
D |
| 38. |
 In the diagram, PS and RS are tangents to the circle centre O, A. 110\(^o\) B. 135\(^o\) C. 165\(^o\) D. 225\(^o\) |
|
| 39. |
 In the diagram, WXYZ is a rectangle with diamension 8cm by 6cm. P, Q, R and S are the midpoints of the rectangle as shown. Using this information calculate the area of the part of the rectangle that is not shaded A. 25cm\(^2\) B. 24cm\(^2\) C. 16cm\(^2\) D. 12cm\(^2\) |
|
| 40. |
 The solution of x + 2 \(\geq\) 2x + 1 is illustrated A. i B. ii C. iii D. iv Detailed Solutionx + 2 \(\geq\) 2x + 1x - 2x \(\geq\) 1 - 2 -x \(\geq\) -1 \(\frac{-x}{-1}\) \(\geq\) \(\frac{-1}{-1}\) x \(\leq\) 1 |